《概率论与数理统计》课程教学课件（PPT讲稿）第五章 大数定律及中心极限定理 5.1 大数定律

概華论与款醒硫外 引言 迄今为止，人们已发现很多大数定律 (laws of large numbers),所谓大数定律， 简单地说，就是大量数目的随机变量所 呈现出的规律，这种规律一般用随机变 量序列的某种收敛性来刻划。本章仅介 绍几个最基本的大数定律

引言 迄今为止,人们已发现很多大数定律 (laws of large numbers)，所谓大数定律， 简单地说，就是大量数目的随机变量所 呈现出的规律，这种规律一般用随机变 量序列的某种收敛性来刻划。本章仅介 绍几个最基本的大数定律

概车纶与款理统外 S5.1大数定律 》讨论 “概率是频率的稳定值”的确切含义； >给出几种大数定律： 切比雪夫大数定律 伯努利大数定律 辛钦大数定律

§5.1 大数定律 ➢ 讨论 “概率是频率的稳定值”的确切含义； ➢ 给出几种大数定律： 切比雪夫大数定律 伯努利大数定律 辛钦大数定律

概華论与款醒硫外 一、问题的引入 实例 频率的稳定性 随着试验次数的增加，事件发生的频率逐渐稳 定于某个常数 启示：从实践中人们发现大量测量值的算术 平均值有稳定性

一、问题的引入 实例 频率的稳定性 随着试验次数的增加, 事件发生的频率逐渐稳 定于某个常数. 启示: 从实践中人们发现大量测量值的算术 平均值有稳定性

概车纶与款理统外 二、基本定理 定理一（切比雪夫大数定律) 设随机变量X1,X2,.,Xn,.相互独立， 且具有相同的数学期和方差：E(X)=4, D(Xk)=o2(k=1,2,),作前n个随机变量 的算术平均X=!∑X,则对于任意正 数ε有 1x-k=空-i h-→∞

二、基本定理 定理一（切比雪夫大数定律） 数 有 的算术平均 则对于任意正 作 前 个随机变量 且具有相同的数学期望和方差： 设随机变量 相互独立    , 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2 = = = = = n k k k k n X n X D X k n E X X X X    1. 1 lim {| | } lim 1 =       −  =  −  = → →     n k k n n X n P X P

概華论与款醒硫外「 说明： 当n很大时，随机变量X1,X2,X,n的算术平 均之水接近于数学期望 nk=1 E(X1)=E(X2)=.=E(Xk)=4, (这个接近是概率意义下的接近) 即在定理条件下，n个随机变量的算术平均，当n 无限增加时，几乎变成一个常数

说明: ( ) ( ) ( ) , 1 , , , , 1 2 1 1 2 = = = =  = k n k k n E X E X E X X n n X X X   均 接近于数学期望 当 很大时 随机变量 的算术平 （这个接近是概率意义下的接近） 即在定理条件下, n个随机变量的算术平均, 当n 无限增加时, 几乎变成一个常数

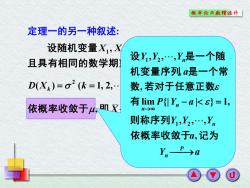
概车纶与款理统外 定理一的另一种叙述： 设随机变量X1,X 且具有相同的数学期 设Y,上2，.，Yn是一个随 机变量序列是一个常 D(X)=o2(k=1,2, 数，若对于任意正数8 依概率收敛于4，肌又 有lim P(Y-aK}=1, 则称序列Y1,Y2,.,Y 依概率收敛于，记为

, . 1 ( ) ( 1, 2, ), ( ) , , , , , , 1 2 1 2     ⎯→ = = = = = P n k k k k n X X n D X k X E X X X X 依概率收敛于 即 则序列 且具有相同的数学期望和方差： 设随机变量 相互独立    Y a a Y Y Y P Y a a Y Y Y P n n n n n ⎯→ −  = → 依概率收敛于 记 为 则称序列 有 数 若对于任意正数 机变量序列 是一个常 设 是一个随 , , , , lim {| | } 1, , , , , , 1 2 1 2     定理一的另一种叙述:

概華论与款醒统外 依概率收敛序列的性质： 设XnP→a,YnP→b, 又设函数g(K,y)在点(a,b)连续， 则g(Xm,Yn)P→g(a,b)

依概率收敛序列的性质: ( , ) ( , ) , , , 又设函数 在 点 连 续 设 g x y a b X a Y b P n P n ⎯→ ⎯→ g(X ,Y ) g(a, b). P 则 n n ⎯→

概车纶与款理统外 定理二（伯努利大数定理) 设n4是n次独立重复试验中事件A发生 的次数，p是事件A在每次试验中发生的率， 则对于任意正数ε>0，有 =P:p<小=1或r只-p2-0

lim 1 lim 0. 0, , , =       = −        −   → →    p n n p P n n P p A n n A A n A n A 或 则对于任意正数 有 的次数 是事件 在每次试验中发生的概率 设 是 次独立重复试验中事件 发 生 定理二（伯努利大数定理）

概華论与款醒硫外 说明： 伯努利定理表明事件发生的频率”4依概 n 率收于事件的概率p,它以严格的数学形式 表达了频率的稳定性. 故而当n很大时，事件发生的频率与概率 有较大偏差的可能性很小.在实际应用中，当试 验次数很大时，便可以用事件发生的频率来代 替事件的概率

说明: . , 表达了频率的稳定性 率收敛于事件的概率 它以严格的数学形式 伯努利定理表明事件发生的频率 依概 p n nA 故而当 n 很大时, 事件发生的频率与概率 有较大偏差的可能性很小. 在实际应用中, 当试 验次数很大时, 便可以用事件发生的频率来代 替事件的概率

概车纶与款理统外 定理三（辛钦定理) 设随机变量X1,X2,.,Xm,.相互独立， 服从同一分布，且具有数学期望E(Xk)=4 (k=1,2,., 则对于任意正数云有P得空-小<小- 关于辛钦定理的说明： (1)与定理一相比，不要求方差存在； (2)伯努利定理是辛钦定理的特殊情况

( 1,2, ), , ( ) , , , , , 1 2    = = k E X X X X k n 服从同一分布 且具有数学期望  设随机变量 相互独立 1. 1 , lim 1 =        −  = →    n k k n X n 则对于任意正数 有 P 关于辛钦定理的说明: (1) 与定理一相比, 不要求方差存在; (2) 伯努利定理是辛钦定理的特殊情况. 定理三（辛钦定理）