《概率论与数理统计》课程教学课件（PPT讲稿）第三章 多维随机变量及其分布 3.2 边缘分布

第二节 边缘分布 一、边缘分布函数 二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘概率密度

二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘概率密度 一、边缘分布函数 第二节 边缘分布

一、边缘分布函数 问题：已知(X,Y)的分布，如何确定X的分布？ D F(x,y)=P{X≤x,Y≤y},Fx(x)=P{X≤x}, P{X≤x=P{X≤x,Y<o}=F(x,∞)=Fx(x) n X,Y)关于X的边缘分布函数

一、边缘分布函数 F(x, y) = P{X  x,Y  y}, F (x) P{X x}, X =  P{X  x} = P{X  x,Y  } = F(x,) F (x) = X (X,Y )关于X的边缘分布函数. 问题:已知(X,Y)的分布,如何确定 X 的分布?

定义设F(x,y)为随机变量(X,Y)的分布函数， 则F(x,y)=P{X≤x,Y≤y}. 令y→o,称P{X≤x}=P{X≤x,Y<∞}=F(x,∞) 为随机变量(X,Y)关于X的边缘分布函数. 记为Fx(x)=F(x,o), 同理令x→0， F(y)=F(o,y)=P{X<o,Y≤y}=P{Y≤y} 为随机变量(X,Y)关于Y的边缘分布函数

F ( y) F( , y) P{X ,Y y} P{Y y} Y =  =    =  为随机变量 ( X,Y )关于Y 的边缘分布函数. ( , ) . , { } { , } ( , ) ( , ) { , }. ( , ) ( , ) , 为随机变量 关 于 的边缘分布函数 令 称 则 设 为随机变量 的分布函数 X Y X y P X x P X x Y F x F x y P X x Y y F x y X Y →   =    =  =   F (x) = F(x,). 记为 X 定义 同理令 x → 

二、离散型随机变量的边缘分布律 定义 设二维离散型随机变量X,Y)的联合分布 律为 P{X=x,Y=yj}=p,i,j=1,2,. 记 n.=2,=PX=x,i=1,2 i= n=∑p与=PY=yh,j=1,2, i=1 分别称p.(i=1,2,)和p,(j=1,2,.)为(X,Y) 关于X和关于Y的边缘分布律

. ( 1,2, ) ( 1,2, ) ( , ) { }, 1,2, , { }, 1,2, , { , } , , 1,2, . ( , ) 1 1 关 于 和关于 的边缘分布律 分别称 和 为 记 律 为 设二维离散型随机变量 的联合分布 X Y p i p j X Y p p P Y y j p p P X x i P X x Y y p i j X Y i j j i j ij i j i ij i j ij      = = = = = = = = = = = = = = • •  = •  = •   定义 二、离散型随机变量的边缘分布律

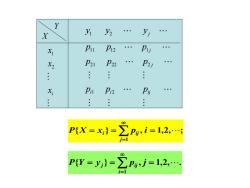
Y X y X1 P11P2 Pu X2 P21 P22 Pzi X Pa Pi2 . Pi P{X=}=∑Pg,i=1,2,. P{Y=y}=∑P,j=1,2

{ } , 1,2, ; 1 = =  =   = P X x p i j i ij { } , 1,2, . 1 = =  =   = P Y y p j i j ij X Y 1 2 i x x x 1 2 j y y y 11 12 1 21 22 2 1 2 j j i i ij p p p p p p p p p

例1已知下列联合分布律求其边缘分布律， 2 0.1 0.3 1 0.10.05 0.45 注意 联合分布 士边缘分布

例1 已知下列联合分布律求其边缘分布律. X Y −1 0 2 1 0 0.1 0.3 0 0.1 0.05 0.45 注意 联合分布 边缘分布

三、连续型随机变量的边缘概率密度 定义对于连续型随机变量(X,Y),设它的概率 密度为f(x,y),由于 Fx(x)=F(x,)=f(x,y)dyldx, 记 fx(x)=Jf(x,y)dy, 称其为随机变量(X,Y)关于X的边缘概率密度

( , ) . ( ) ( , )d , ( ) ( , ) [ ( , )d ]d , ( , ), ( , ), 称其为随机变量 关 于 的边缘概率密度 记 密度为 由 于 对于连续型随机变量 设它的概率 X Y X f x f x y y F x F x f x y y x f x y X Y X x X     − −  − = =  = 定义 三、连续型随机变量的边缘概率密度

同理可得Y的边缘概率密度 F()=F()dy, f(y)-[f(x.y)dx. Y的边缘概率密度

同理可得 Y 的边缘概率密度 ( ) ( , )d .  + − fY y = f x y x Y 的边缘概率密度. ( ) ( , ) ( , )d d , −  + − =  = y Y F y F y f x y x y

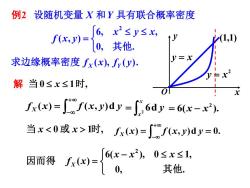
例2设随机变量X和Y具有联合概率密度 f(x,y)= [6,x2≤y≤x, 0,其他. 求边缘概率密度fx(x),f(y): 解当0≤x≤1时， fx(x)=f(x,y)dy=[6dy=6(x-x2) 当x1时，fx(x)=∫mf(x,y)dy=0. 因而得fx)=0, J6(x-x2)0≤x≤1， 其他

( ), ( ). 0, . 6, , ( , ) 2 f x f y x y x f x y X Y 求边缘概率密度 X Y 其他 设随机变量 和 具有联合概率密度    = 解 当 0  x  1 时, y = x 2 y = x O x y (1,1) f x f x y y X ( ) ( , )d + − =  = xx y 2 6d 例2 6( ). 2 = x − x 当 x  0 或 x  1时, ( ) = ( , )d = 0. + − f x f x y y X  −   = 0, . 6( ), 0 1, ( ) 2 其他 因而得 x x x fX x

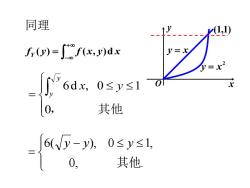
同理 f(y)=[f(x,y)dx 6dx,0sys1- 0, 其他 6(Vy-y)0≤y≤1， 其他

同理fY ( y) f (x, y)d x  + − =     −   = 0, . 6( ), 0 1, 其他 y y y        =  0， 其他 6d x, 0 y 1 y y y = x 2 y = x O x y (1,1)