《概率论与数理统计》课程教学课件（PPT讲稿）第三章 多维随机变量及其分布 3.4 相互独立的随机变量

概车纶与款理统外「 第四节 随机变量的相互独立性 1.定义 设F(x,y)及Fx(x),F,(Oy)分别是二维随机变量 (X,Y)的分布函数及边缘分布函数若对于所有x,y 有 P{X≤x,Y≤y}=P{X≤xP{Y≤y, 即 F(x,y)=Fx(x)Fy(y), 则称随机变量X和Y是相互独立的

. ( , ) ( ) ( ), { , } { } { }, ( , ) . , ( , ) ( ), ( ) 则称随机变量 和 是相互独立的 即 有 的分布函数及边缘分布函 数 若对于所有 设 及 分别是二维随机变量 X Y F x y F x F y P X x Y y P X x P Y y X Y x y F x y F x F y X Y X Y =   =   第四节 随机变量的相互独立性 1.定义

概车纶与款理统外 2.说明 ()若离散型随机变量(X,Y)的联合分布律为 P{X=x,Y=y}=P,ij=1,2,. X和Y相互独立 ←→P{X=x,Y=y}=P{X=x}PY=y, 即p=P.P

 { , } { } { }, i j i j P X = x Y = y = P X = x P Y = y X 和Y 相互独立 2.说明 (1) 若离散型随机变量 ( X,Y )的联合分布律为 P{X = x ,Y = y } = p , i, j =1,2,  . i j i j pi j pi• p• j 即 = 

概華论与款程统外 (2)设连续型随机变量(X,Y)的联合概率密度为 f(x,y),边缘概率密度分别为fx(x),f(y),则有 X和y相互独立台f(x,y)=fx(x)f(y), (3)X和Y相互独立，则 f(X)和g(Y)也相互独立

 f (x, y) f (x) f ( y). = X Y (3) X 和Y 相互独立, 则 X 和Y 相互独立 边缘概率密度分别为 则有 设连续型随机变量 的联合概率密度为 ( , ), ( ), ( ), (2) ( , ) f x y f x f y X Y X Y f (X) 和 g(Y )也相互独立

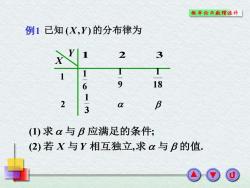
概车纶与款理统外 例1己知(X,Y)的分布律为 2 3 1 T T 6 9 18 1 2 a B (1)求与B应满足的条件； (2)若X与Y相互独立，求α与B的值

例1 已知 (X,Y )的分布律为 (2) , . (1) ; 若 与 相互独立 求 与 的值 求 与 应满足的条件     X Y 1 2 1 2 3 6 1 9 1 18 1 3 1   X Y

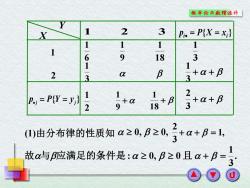
概车纶与款理统外[ 1 2 3 Pi.=P(X=x} 1 1 1 1 6 9 18 3 1 1 2 3 a B +a+B 3 D.=P(Y=y} 1-2 3+a+B (0由分布律的性质知a≥0B≥0子a+B=1 故a与应满足的条件是：a≥0，B≥0且a+B= 3

(1)由分布律的性质知   0,   0, 1, 3 2 + +  = . 3 1 故与应满足的条件是:  0,   0 且 +  = X Y 1 2 3 1 2 6 1 9 1 18 1 3 1   { } i i p = P X = x • 3 1 + +  3 1 { } j j p = P Y = y • 2 1 + 9 1 +  18 1 + +  3 2

概车纶与款理统外「 (2)因为X与Y相互独立，所以有 P=p.·p9(i=1,2;广=1,2,3) 特别有 p=→写g+a小a=号 又a+B=3得B=g

=  , ( = 1,2; = 1,2,3) • • p p p i j ij i j 特别有 12 1• •2 p = p  p        = + 9 1 3 1 9 1 , 9 2   = 又 , 3 1  +  = . 9 1 得  = (2) 因为 X 与 Y 相互独立, 所以有

概華论与款醒硫外 例2设两个独立的随机变量X与Y的分布律为 3 Y2 4 Px 0.3 0.7 0.6 0.4 求随机变量(X,Y)的分布律

求随机变量 ( X, Y ) 的分布律. 例2 设两个独立的随机变量 X 与Y 的分布律为 X PX 1 3 0.3 0.7 Y PY 2 4 0.6 0.4

概车纶与款理统外「 例3一负责人到达办公室的时间均匀分布在8~12 时，他的秘书到达办公室的时间均匀分布在7~9时， 设他们两人到达的时间相互独立，求他们到达办 公室的时间相差不超过5分钟的概率. 解设X和Y分别是负责人和他的秘书到 达办公室的时间，由假设X和Y的概率密度分别为 人倒-其2m=2e9 0,其它， 0,其它， 由于X,Y相互独立，得(X,Y)的概率密度为

例3 一负责人到达办公室的时间均匀分布在8~12 时,他的秘书到达办公室的时间均匀分布在7~9时, 设他们两人到达的时间相互独立, 求他们到达办 公室的时间相差不超过 5 分钟的概率. 解 达办公室的时间, 设 X 和Y 分别是负责人和他的秘书到 由假设X 和Y的概率密度分别为      = 0, , 1 4, 8 12, ( ) 其它 x fX x      = 0, , 1 2, 7 9, ( ) 其它 x f y Y 由于 X,Y 相互独立, 得 (X,Y)的概率密度为

概華伦与款醒统外 f(x,y)=fx(x)f(y) =18,8<x<12,7<y<9, 0,其它. PX-Y≤1/12} =J∬fx,y)dxdy B =×(G的面积) 8 12x

f (x, y) f (x) f ( y) = X Y        = 0, . 1 8, 8 12,7 9, 其它 x y P{ X −Y  1 12}  = G f (x, y)d xd y ( ). 8 1 =  G 的面积 O x y • 8 • 12 7 9 A B B C C G

概车纶与款理统外 而( G的面积=△ABC的面积-△AB'C的面积 8-调-。花 于是P1X-Y≤1/12 8 12x =x(G的面积)= 1 8 8 因此负责人和他的秘书到达办公室的时间相差 不超过5分钟的概率为 8

而 G的面积 = ABC的面积− ABC的面积 2 2 12 11 2 1 12 13 2 1        −      = . 6 1 = 于是 P{ X −Y  1 12} ( ) 8 1 =  G 的面积 . 48 1 = . 48 1 不超过5分钟的概率为 因此负责人和他的秘书到达办公室的时间相差 O x y • 8 • 12 7 9 A B B C C G