《概率论与数理统计》课程教学课件（习题课，PPT）第一章 概率论的基本概念

第一章概率论的基本概念 习题课 一、本章内容 二、典型例题

一、本章内容 二、典型例题 第一章 概率论的基本概念 习 题 课

1.主要概念： 样本空间：随机试验的所有可能结果组成 的集合。 随机事件：样本空间S的子集。 基本事件：只含一个样本点的事件。 概率： 满足非负性、规范性、可列可 加性的集合函数

1. 主要概念： 样本空间：随机试验的所有可能结果组成 的集合。 随机事件：样本空间S的子集。 基本事件：只含一个样本点的事件。 概率： 满足非负性、规范性、可列可 加性的集合函数

A,B互不相容： A、B不能同时发生，即AB=办 A,B相互独立： A、B的发生互不影响。P(AB)=P(A)P(B)

A B AB 、 不能同时发生，即 = A B P AB P A P B 、 的发生互不影响。 ( ) ( ) ( ) = A B, 互不相容： A B, 相互独立：

2.主要公式： 加法公式： P(AUB)=P(A)+P(B)-P(AB) 差事件公式： P(A-B)=P(A)-P(AB)=P(AB) 逆事件公式： P(A)=1-P(A)

2.主要公式： 加法公式： 差事件公式： 逆事件公式： P A B P A P B P AB ( ) ( ) ( ) ( ) = + − P A B P A P AB P AB ( ) ( ) ( ) ( ) − = − = P A P A ( ) 1 ( ) = −

条件概率： P(AIB)= P(AB) P(B) 乘法公式： P(AA2.An)=P(A)P(A2|A.P(AAA.An) 全概率公式： PAD=∑PAB)P(B) 贝叶斯公式： P(B14)= P(AB,)P(B,)P(AB,)P(B,) P(A) ∑P(AIB,)P(B)

条件概率： 乘法公式： 全概率公式： 贝叶斯公式： ( ) ( | ) ( ) P AB P A B P B = 1 2 1 2 1 1 2 1 ( ) ( ) ( | ) ( | ) P A A A P A P A A P A A A A n n n = − 1 ( ) ( | ) ( ) n i i i P A P A B P B = =  1 ( | ) ( ) ( | ) ( ) ( | ) ( ) ( | ) ( ) i i i i i n i i i P A B P B P A B P B P B A P A P A B P B = = = 

例1选择题 1.设P(AB)=0,则 (A)A和B不相容 (B/A,B相互独立 (C)P(4)=O或P(B)=0 P(A-B)=P(A) 2.设AcB,且相互独立，则 (A)P(A)=0 (B)P(A)=0或P(A)=1 (C)P(A)=1 (p)P()=0减P(B)=1

例1 选择题 1.设P AB ( ) 0, = 则 ( ) A A B 和 不相容 ( ) , B A B相互独立 ( ) ( ) 0 ( ) 0 C P A P B = = 或 ( ) ( ) ( ) D P A B P A − = 2. , 设A B  且相互独立，则 ( ) ( ) 0 A P A = ( ) ( ) 0 ( ) 1 B P A P A = = 或 ( ) ( ) 1 C P A = ( ) ( ) 0 ( ) 1 D P A P B = = 或 √ √

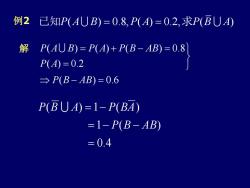
例2已知P(AUB)=0.8,P(A)=0.2,求P(BUA) 解 P(AUB)=P(A)+P(B-AB)=0.8 P(A)=0.2 →P(B-AB)=0.6 P(BUA)=1-P(BA) =1-P(B-AB) =0.4

例 2 已 知P A B P A P B A ( ) 0.8, ( ) 0.2, ( ) = = 求 解 ( ) ( ) ( ) 0.8 ( ) 0.2 ( ) 0.6 P A B P A P B AB P A P B AB = + − =  =   − = 0.4 1 ( ) ( ) 1 ( ) == − − = − P B AB P B  A P BA

例3：盒中放有12个乒乓球，其中9个是新的，3 个是旧的。第一次比赛时从中任取3个来用，比 赛后仍放回盒中。第二次比赛时再从盒中任取3 个，求第二次取出的球都是新球的概率。 解：记B={第一次比赛时取出个新球}i=0,1,2,3 A={第二次取出的都是新球}

例3：盒中放有12个乒乓球，其中9个是新的，3 个是旧的。第一次比赛时从中任取3个来用，比 赛后仍放回盒中。第二次比赛时再从盒中任取3 个，求第二次取出的球都是新球的概率。 解： { } 0,1,2,3 { } B i i i A = = = 记 第一次比赛时取出 个新球 第二次取出的都是新球

P(B) 230 P(AB) P(B) P(AB) P(B2) 器 P(A川B)= 格鸡60500功 P(B,) P(A|B)= 所以P(A)= P(BP(AE) 1 84, 2756,108 35.84 20 ≈0.1458 220220220220 220220220220

3 3 3 9 0 0 3 3 12 12 1 84 ( ) ( | ) 220 220 C C P B P A B C C = = = = 1 2 3 9 3 8 1 1 3 3 12 12 27 56 ( ) ( | ) 220 220 C C C P B P A B C C = = = = 2 1 3 9 3 7 2 1 3 3 12 12 108 35 ( ) ( | ) 220 220 C C C P B P A B C C = = = = 3 3 9 6 3 3 3 3 12 12 84 20 ( ) ( | ) 220 220 C C P B P A B C C = = = = 3 0 ( ) ( ) ( | ) 1 84 27 56 108 35 84 20 0.1458 220 220 220 220 220 220 220 220 i i i P A P B P A B = = =  +  +  +   所以 

例4假设目标出现在射程之内的概率为07，这时 射击命中目标的概率为0.6，试求两次独立射击至 少有一次命中目标的概率 [思路]引进事件 A=但标进入射程； B={第次射击命中日标，i=1,2 故所求概率为事件B=BUB,的概率，由于目标 不在射程之内是不可能命中目标的，因此，可利 用全概率公式来求解

0.7, 0.6, . 假设目标出现在射程之内的概率为 这时 射击命中目标的概率为 试求两次独立射击至 少有一次命中目标的概率 [思路] 引进事件 A={ }; 目标进入射程 { }, 1,2. B i i i = = 第 次射击命中目标 1 2 , , , . 故所求概率为事件B B B = 的概率 由于目标 不在射程之内是不可能命中目标的 因此 可利 用全概率公式来求解 例4