《概率论与数理统计》课程教学课件（PPT讲稿）第五章 大数定律及中心极限定理 5.2 中心极限定理

引言 概華伦与款醒硫外 在随机变量的一切可能的分布律中，正态分布占 有特殊重要的地位.实践中经常遇到的大量的随机 变量都是服从正态分布的就提出这样的问题： 1、为什么正态分布如此广泛地存在，从而在概 率论中占有如此重要的地位？ 2、应该如何解释大量随机现象中的这一客观规 律呢？ 概率论中有关论证随机变量之和的极限分布为 正态分布的定理称为中心极限定理

引言 在随机变量的一切可能的分布律中,正态分布占 有特殊重要的地位.实践中经常遇到的大量的随机 变量都是服从正态分布的.就提出这样的问题: 1、为什么正态分布如此广泛地存在,从而在概 率论中占有如此重要的地位? 2、应该如何解释大量随机现象中的这一客观规 律呢？ 概率论中有关论证随机变量之和的极限分布为 正态分布的定理称为中心极限定理

概车伦与散理统外「 §5.2 中心极限定理 独立随机变量和 设{X}为独立随机变量序列，记其和为 合x 讨论独立随机变量和的极限分布 >指出极限分布为正态分布

§5.2 中心极限定理 ➢ 讨论独立随机变量和的极限分布 ➢ 指出极限分布为正态分布 独立随机变量和 设 {Xn} 为独立随机变量序列，记其和为 1 n k k X = 

概華伦与款程统外 一、问题的引入 实例：考察射击命中点与靶心距离的偏差 这种偏差是大量微小的偶然因素造成的微 小误差的总和，这些因素包括：瞄准误差、测量 误差、子弹制造过程方面（如外形、重量等）的 误差以及射击时武器的振动、气象因素（如风速、 风向、能见度、温度等)的作用，所有这些不同 因素所引起的微小误差是相互独立的，并且它们 中每一个对总和产生的影响不大。 问题：某个随机变量是由大量相互独立且均匀 小的随机变量相加而成的，研究其概率分布情况

一、问题的引入 实例: 考察射击命中点与靶心距离的偏差. 这种偏差是大量微小的偶然因素造成的微 小误差的总和, 这些因素包括: 瞄准误差、测量 误差、子弹制造过程方面 (如外形、重量等) 的 误差以及射击时武器的振动、气象因素(如风速、 风向、能见度、温度等) 的作用, 所有这些不同 因素所引起的微小误差是相互独立的, 并且它们 中每一个对总和产生的影响不大. 问题: 某个随机变量是由大量相互独立且均匀 小的随机变量相加而成的, 研究其概率分布情况

概车纶与款理统外 二、基本定理 定理四（独立同分布的中心极限定理） 设随机变量X1,X2,.,Xm,.相互独立服从 同一分布，且具有数学期望和方差：E(X)=4, D(X)=o2>0(k=1,2,则随机变量之和的 立x-2xx-w 标准化变量Y,= k=1 2x

二、基本定理 定理四（独立同分布的中心极限定理） 则随机变量之和的 同一分布 且具有数学期望和方差： 设随机变量 相互独立 服 从 ( ) 0 ( 1,2, ), , ( ) , , , , , , 2 1 2    =  = = D X k E X X X X k k n               − =    = = = n k k n k k n k k n D X X E X Y 1 标准化变量 1 1   n X n n k k − = =1

概率伦与款理统外 的分布函数F(x)对于任意x满足 :-nu lim F(x)=limP间 ≤x 1-→00 n-→o0 √no 定理四表明： 当n→oo,随机变量序列Yn的分布函数收敛于 标准正态分布的分布函数

               − = = → → x n X n F x P F x x n k k n n n n   1 lim ( ) lim 的分布函数 ( ) 对于任意 满 足 定理四表明: . , 标准正态分布的分布函数 当 n →  随机变量序列Yn 的分布函数收敛于 − − = = x t e dt (x). 2π 1 2 2 

概车纶与款理统外 定理五（李雅普诺夫中心极限定理） 设随机变量X1,X2,.,Xm,.相互独立，它 们具有数学期望和方差： E(Xk)=4k,D(Xk)=Ok2≠0(k=1,2,), 记 B=∑o, k=1 若存在正数6，使得当n→o时， 度2X-)→0

{| | } 0, 1 , , , ( ) , ( ) 0 ( 1,2, ), , , , , , 1 2 2 1 2 2 2 1 2 − → →  = = =  =   = + + = n k k k n n k n k k k k k n E X B n B E X D X k X X X        若存在正数 使得当 时 记 们具有数学期望和方差： 设随机变量 相互独立 它    定理五(李雅普诺夫中心极限定理)

概率伦与款醒统外「 则随机变量之和的标准化变量 x-2x2x-24 k=1 2x B 的分布函数F(x)对于任意x满足 ∑x-∑4 lim F((x)=lim P每 k=1 ≤X〉 B

则随机变量之和的标准化变量             − =    = = = n k k n k k n k k n D X X E X Z 1 1 1 n n k k n k k B X  = = − = 1 1  的分布函数Fn (x)对于任意x满足                − =   = = → → x B X F x P n n k k n k k n n n 1 1 lim ( ) lim  − − = = x t e dt (x). 2π 1 2 2 

概车纶与款理统外 定理五表明： 无论各个随机变量X1,X2,.,Xm,.服从什么 分布，只要满足定理的条件，那么它们的和∑X。 k=1 当n很大时，近似地服从正态分布. (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况

定理五表明: , . , , , , , , 1 1 2 当 很大时 近似地服从正态分布 分布 只要满足定理的条件 那么它们的和 无论各个随机变量 服从什么 n X X X X n k k n =   (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况

概華伦与款醒统外 定理六（德莫佛一拉普拉斯定理） 设随机变量nn(n=1,2,)服从参数为n,p (0<p<1)的二项分布，则对于任意x,恒有 Pas小-上2=oa -→o 定理六表明： 正态分布是二项分布的极限分布，当n充分大 时，可以利用该定理来计算二项分布的概率

− − → = =        − −   = x t n n n x t x np p np P p x n n p e d ( ). 2π 1 (1 ) lim (0 1) , , ( 1,2, ) , 2 2    的二项分布 则 对于任意 恒有 设随机变量  服从参数为 定理六(德莫佛－拉普拉斯定理) 定理六表明: 正态分布是二项分布的极限分布, 当n充分大 时, 可以利用该定理来计算二项分布的概率

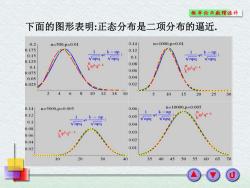
概车纶与款理统外 下面的图形表明：正态分布是二项分布的逼近. 0.2 n=500,p=0.01 0.14 n=1000,p=0.01 0.175 k-np 0.12 0.15 k-np Vnpq Vnpq 0.1 0.125 p'g Vnpq 0.08 0.1 0.075 0.06 0.05 0.04 0.025 0.02 8 10 10 15 20 25 30 0.14 n=5000,p=0.005 0.06 n=10000,p=0.005 k np 0.12 1 k np 0.05 pd-k 0.1 npq 0.04 0.08 0.06 0.03 0.04 0.02 0.02 0.01 10 20 % 35 40 455055 60 65 70

下面的图形表明:正态分布是二项分布的逼近