《概率论与数理统计》课程教学课件（习题课，PPT）第二章 随机变量及其分布

概车纶与款理统外 第二章 随机变量及其分布 习题课 一、重点与难点 二、主要内容 三、典型例题

一、重点与难点 二、主要内容 三、典型例题 第二章 随机变量及其分布 习 题 课

概率伦与款理统外 一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的密度函数 及有关概率的计算 2.难点 随机变量的分布函数的求法 连续型随机变量的函数的分布

一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的密度函数 及有关概率的计算 2.难点 随机变量的分布函数的求法 连续型随机变量的函数的分布

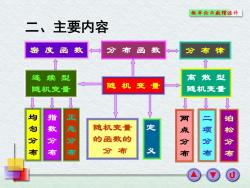
概车纶与款理统外 二、主要内容 密度 函 数 分布函数 布律 连续型 离散型 随机变量 随机变量 随机变量 均匀分布 指教分布 正态分布 随机变量 定 的函数的 点分布 项 习 分布 布 松分布

二、主要内容 随 机 变 量 离 散 型 随机变量 连 续 型 随机变量 密 度 函 数 分 布 函 数 分 布 律 均 匀 分 布 指 数 分 布 正 态 分 布 两 点 分 布 二 项 分 布 泊 松 分 布 随机变量 的函数的 分 布 定 义

概華论与款醒硫外 随机变量 定义设E是随机试验，它的样本空间是S={}.如 果对于每一个eeS,有一个实数X(e)与之对应，这 样就得到一个定义在S上的单值实值函数X(),称 随机变量. ()随机变量与普通的函数不同 (2)随机变量的取值具有一定的概率规律 (3)随机变量与随机事件的关系

. ( ), , ( ) , , { }. 随机变量 样就得到一个定义在 上的单值实值函数 称 果对于每一个 有一个实数 与之对应 这 定义 设 是随机试验 它的样本空间是 如 S X e e S X e E S e  = (1)随机变量与普通的函数不同 随机变量 (2)随机变量的取值具有一定的概率规律 (3)随机变量与随机事件的关系

概车纶与款理统外 随机变量的分类 随机变量 离散型 非离散型 连续型 其它 随机变量所取的可能值是有限多个或无限 可列个，叫做离散型随机变量

随机变量的分类 离散型 随机变量 连续型 非离散型 其它 随机变量所取的可能值是有限多个或无限 可列个, 叫做离散型随机变量

概華论与款醒统外 离散型随机变量的分布律 ()定义 设离散型随机变量X所有可能取的值为xx (k=1,2,),X取各个可能值的概率，即事件 {X=x}的概率，为 P{X=Xk}=pk,k=1,2,. 称此为离散型随机变量X的分布律

. { } , 1,2, . { } , ( 1,2, ), , 称此为离散型随机变量 的分布律 的概率 为 取各个可能值的概率 即事件 设离散型随机变量 所有可能取的值为 X P X x p k X x k X X x k k k k   = = = = = 离散型随机变量的分布律 (1)定义

概车纶与款理统外 (2)说明 1°pk≥0，k=1,2, 00 2”∑p&=l5 k=1 3离散型随机变量的分布律也可表为 X x12. Xn P P2 X 2.xn. Pk PP.Pm

          n n p p p x x x X 1 2 1 2 ~ X pk x1 x2  xn  p1 p2  pn  1 0, 1,2, ; 0 pk  k =  2 1; 1 0  =  k= pk (2)说明 3 0离散型随机变量的分布律也可表为

概華论与款醒统外 两点分布 设随机变量X只可能取0与1两个值，它的分 布律为 X 0 1 P& 1-p 则称X服从(0-1)分布或两点分布

设随机变量 X 只可能取0与1两个值 , 它的分 布律为 X pk 0 1− p 1 p 则称 X 服从(0-1)分布或两点分布. 两点分布

概车纶与款理统外 二项分布 X的分布律为 P{X=}=Cp(I-p)”- (k=0,1,2,.,n,0<p<1) 称这样的分布为二项分布.记为X~(n,p). 二项分布 n=1. 两点分布

称这样的分布为二项分布.记为 X ~ b(n, p). X的分布律为 (k = 0,1,2,  ,n, 0  p  1) 二项分布 n = 1 两点分布 二项分布 { } (1 ) k k n k P X k C p p n − = = −

概華论与款醒硫外 泊松分布 设随机变量所有可能取的值为0,1,2，.，而取 各个值的概率为 P==e e! ,k=0,1,2,.) 其中入>0是常数.则称X服从参数为入的泊松分 布，记为X~(2)

, ~ π( ). 0 . , 0,1,2, , ! e { } 0,1,2, ,      X X k k P X k k 布 记为 其中 是常数 则称 服从参数为 的泊松分 各个值的概率为 设随机变量所有可能取的值为 而取  = = = −   泊松分布