《概率论与数理统计》课程教学资源（知识点与公式）概率论与数理统计概率部分知识点总结

第1章随机事件及其概率 m pn= 从m个人中挑出n个人进行排列的可能数。 (1)排列 (m-n)! 组合公式 C0= 从m个人中挑出n个人进行组合的可能数。 l(m-nj训 加法原理（两种方法均能完成此事）：m+n (2)加法 某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由 种方法来完成，则这件事可由mn种方法来完成。 和乘法原 乘法原理（两个步骤分别不能完成这件事）：m×n 理 某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由 种方法来完成，则这件事可由m×种方法来完成。 重复排列和非重复排列（有序） (3)一些 常见排列 对立事件（至少有一个） 顺序问题 如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个， (4)随机 试验和随 但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试 验。 机事件 试验的可能结果称为随机事件。 在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有 如下性质： ①每进行一次试验，必须发生且只能发生这一组中的一个事件： (5)基本 ②任何事件，都是由这一组中的部分事件组成的。 事件、样本 这样一组事件中的每一个事件称为基本事件，用0来表示。 空间和事 基本事件的全体，称为试验的样本空间，用2表示。 个事件就是由Q中的部分点（基本事件0）组成的集合。通常用大写字母 A,BC,.表示事件，它们是2的子集。 2为必然事件，0为不可能事件。 不可能事件(0)的概率为零，而概率为零的事件不一定是不可能事件：同理， 必然事件(Q)的概率为1，而概率为1的事件也不一定是必然事件。 ①关系， 如果事件A的组成部分也是事件B的组成部分，(A发生必有事件B发生)： 如果同时有ACB,B一A,则称事件A与事件B等价，或称A等于品B (6)事件 A、B中至少有一个发生的事件：4UB,或者什B。 的关系与属于A而不属于B的部分所构成的事件，称为A与B的差，记为A品，也可表 运算 示为A-AB或者AB,它表示A发生而B不发生的事件。 A、B同时发生：A门B或者AB。A门=0，则表示A与B不可能同时发生，称 事件A与事件B互不相容或者互斥。基本事件是互不相容的

1 第 1 章 随机事件及其概率 （1）排列 组合公式 ( )! ! m n m P n m − = 从 m 个人中挑出 n 个人进行排列的可能数。 !( )! ! n m n m C n m − = 从 m 个人中挑出 n 个人进行组合的可能数。 （2）加法 和乘法原 理 加法原理（两种方法均能完成此事）：m+n 某件事由两种方法来完成，第一种方法可由 m 种方法完成，第二种方法可由 n 种方法来完成，则这件事可由 m+n 种方法来完成。 乘法原理（两个步骤分别不能完成这件事）：m×n 某件事由两个步骤来完成，第一个步骤可由 m 种方法完成，第二个步骤可由 n 种方法来完成，则这件事可由 m×n 种方法来完成。 （3）一些 常见排列 重复排列和非重复排列（有序） 对立事件（至少有一个） 顺序问题 （4）随机 试验和随 机事件 如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个， 但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试 验。 试验的可能结果称为随机事件。 （5）基本 事件、样本 空间和事 件 在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有 如下性质： ①每进行一次试验，必须发生且只能发生这一组中的一个事件； ②任何事件，都是由这一组中的部分事件组成的。 这样一组事件中的每一个事件称为基本事件，用  来表示。 基本事件的全体，称为试验的样本空间，用  表示。 一个事件就是由  中的部分点（基本事件  ）组成的集合。通常用大写字母 A，B，C，.表示事件，它们是  的子集。  为必然事件，Ø 为不可能事件。 不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理， 必然事件（Ω）的概率为 1，而概率为 1 的事件也不一定是必然事件。 （6）事件 的关系与 运算 ①关系： 如果事件 A 的组成部分也是事件 B 的组成部分，（A 发生必有事件 B 发生）： A  B 如果同时有 A  B ，B  A ，则称事件 A 与事件 B 等价，或称 A 等于 B：A=B。 A、B 中至少有一个发生的事件：A  B，或者 A+B。 属于 A 而不属于 B 的部分所构成的事件，称为 A 与 B 的差，记为 A-B，也可表 示为 A-AB 或者 AB ，它表示 A 发生而 B 不发生的事件。 A、B 同时发生：A  B，或者 AB。A  B=Ø，则表示 A 与 B 不可能同时发生，称 事件 A 与事件 B 互不相容或者互斥。基本事件是互不相容的

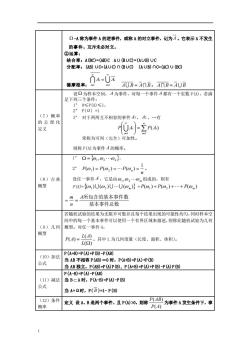
2-A称为事件A的逆事件，或称A的对立事件，记为A。它表示A不发生 的事件。互斥未必对立。 ②运算； 结合率：A(BC)=(AB)C AU(BUC)=(AUB)UC 分配率：(AB)UC-AUC)nBUC)(aUB)nC(AC)UBC) 德摩根率： ∩a=0Ua AUB=A∩B,A∩B=AUB 设2为样本空间，A为事件，对每一个事件A都有一个实数P(),若满 足下列三个条件： P(2)=1 (7)概率 的公理化 3°对于两两互不相容的事件A,.有 定 0-2 常称为可列（完全）可加性。 则称P(A)为事件A的概率。 1°2=，02.0n} gPo-Pre,）o- (8)古典 设任一事件A,它是由0,020n组成的，则有 概型 P(AJ=@)U(@2)U.U@)=P(@)+P(@2)+.+P(@) m。A所包含的基本事件数 n 基本事件总数 若随机试验的结果为无限不可数并且每个结果出现的可能性均匀，同时样本空 间中的每一个基本事件可以使用一个有界区域来描述，则称此随机试验为几何 对任一事件A, P=分。其中L为几何度量（长度面积、作积。 L(Ω) P(A+B)=P(A)+P(B)-P(AB) (10)加法 公式 当AB不相容P(B)=0时，P(A+B)P(A)P(B) 当AB独立，P(AB)=PP®)，P(A+B)-P)+P⑧)P()PB) P(A-B)=P(A)-P(AB) (11)减法 当BcA时，PA-B)=P(A)-P⑧) 公式 当A=Q时，P(B)=1-P(B) (12)条件 定义设A、B是两个事件，且PW0,则为事件A发生条件下，事 概率 PCA 1

1  -A 称为事件 A 的逆事件，或称 A 的对立事件，记为 A 。它表示 A 不发生 的事件。互斥未必对立。 ②运算： 结合率：A(BC)=(AB)C A∪(B∪C)=(A∪B)∪C 分配率：(AB)∪C=(A∪C)∩(B∪C) (A∪B)∩C=(AC)∪(BC) 德摩根率：    =  = = 1 i 1 i i Ai A A B = A B ， A B = A B （7）概率 的公理化 定义 设  为样本空间， A 为事件，对每一个事件 A 都有一个实数 P(A)，若满 足下列三个条件： 1° 0≤P(A)≤1， 2° P(Ω) =1 3° 对于两两互不相容的事件 A1， A2 ，.有   =  = =        1 1 ( ) i i i P Ai P A 常称为可列（完全）可加性。 则称 P(A)为事件 A 的概率。 （8）古典 概型 1°  = 1 ,2 n ， 2° n P P P n 1 ( ) ( ) ( ) 1 =  2 =  = 。 设任一事件 A ，它是由 1 2  m , 组成的，则有 P(A)=(1 )(2 )( m ) = ( ) ( ) ( ) P 1 + P 2 ++ P  m n m = 基本事件总数 A所包含的基本事件数 = （9）几何 概型 若随机试验的结果为无限不可数并且每个结果出现的可能性均匀，同时样本空 间中的每一个基本事件可以使用一个有界区域来描述，则称此随机试验为几何 概型。对任一事件 A， ( ) ( ) ( )  = L L A P A 。其中 L 为几何度量（长度、面积、体积）。 （10）加法 公式 P(A+B)=P(A)+P(B)-P(AB) 当 AB 不相容 P(AB)＝0 时，P(A+B)=P(A)+P(B) 当 AB 独立，P(AB)=P(A)P(B), P(A+B)=P(A)+P(B)-P(A)P(B) （11）减法 公式 P(A-B)=P(A)-P(AB) 当 B  A 时，P(A-B)=P(A)-P(B) 当 A=Ω时，P( B )=1- P(B) （12）条件 概率 定义 设 A、B 是两个事件，且 P(A)>0，则称 ( ) ( ) P A P AB 为事件 A 发生条件下，事

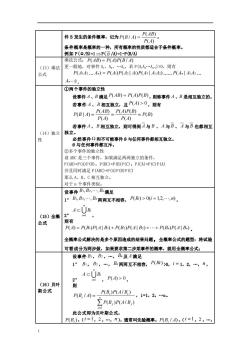
件B发生的条件摄率，记为P(B/)=P八4 P(A) 条件概率是概率的一种，所有概率的性质都适合于条件概率。 例如P(Q/B)=1→P(B/A)=1-PB/A) 乘法公式：P(AB)=P(A0P(BIA) 3)乘法 更一般地，对事件A,A,.A,若P(AA.A-)>0,则有 公式 P(AA.A)=P(A)P(AA)P(431AA2).P(A1AA2. Am-） ①两个事件的独立性 设事件A、B满足P(AB)=P(A)P(B),则称事件A、B是相互独立的。 若事件A、B相互独立，且P(A)>0,则有 PB1A=PM-PPB=P代B P(4) 若事件A、B相互独立，则可得到A与B、A与B、A与B也都相互 (14)独立独立。 性 必然事件卫和不可可能事件与任何事件都相石独立。 日与任何事件都互斥。 ②多个事件的独立性 设ABC是三个事件，如果满足两两独立的条件 P(AB)=P(A)P(B): P(BC)=P(B)P(C):P(CA)=P(C)P(A) 并且同时满足P(ABC)=P(A)P(B)P(C) 那么A、B、C相互种立。 对于n个事件类似。 设率件BLB2,B满足 1°BB,.,B两两互不相容，PB刷>0(=2，川， ACUB. 15)全概 公式 则有 P(A)=P(B)P(AI B)+P(B2)P(AIB2)+.+P(Ba)P(AIB.) 全概率公式解决的是多个原因造成的结果问题，全概率公式的题型：将试验 可看成分为两步做，如果要求第二步某事件的概率，就用全概率公式： 设事件B,B2,B及A满足 1°B1,B2,Bm两两互不相容，P(Bm)>0,i=1,2,n, 4C[B PA0>0, (16)贝叶 多 斯公式 P(B,/A)= P(B.)P(A/B.) P(B)P(AIB) ，i=1,2,.n 此公式即为贝叶斯公式。 P(B),(=1,2,.,n),通常叫先验概率。P(B/A),(i=1,2

1 件 B 发生的条件概率，记为 P(B / A) = ( ) ( ) P A P AB 。 条件概率是概率的一种，所有概率的性质都适合于条件概率。 例如 P(Ω/B)=1  P( B /A)=1-P(B/A) （13）乘法 公式 乘法公式： P(AB) = P(A)P(B / A) 更一般地，对事件 A1，A2，.An，若 P(A1A2.An-1)>0，则有 P(A1A2 . An) = P(A1)P(A2 | A1)P(A3 | A1A2). P(An | A1A2 . An − 1) 。 （14）独立 性 ①两个事件的独立性 设事件 A 、B 满足 P(AB) = P(A)P(B) ，则称事件 A 、B 是相互独立的。 若事件 A 、 B 相互独立，且 P(A)  0 ，则有 ( ) ( ) ( ) ( ) ( ) ( ) ( | ) P B P A P A P B P A P AB P B A = = = 若事件 A 、 B 相互独立，则可得到 A 与 B 、 A 与 B 、 A 与 B 也都相互 独立。 必然事件  和不可能事件 Ø 与任何事件都相互独立。 Ø 与任何事件都互斥。 ②多个事件的独立性 设 ABC 是三个事件，如果满足两两独立的条件， P(AB)=P(A)P(B)；P(BC)=P(B)P(C)；P(CA)=P(C)P(A) 并且同时满足 P(ABC)=P(A)P(B)P(C) 那么 A、B、C 相互独立。 对于 n 个事件类似。 （15）全概 公式 设事件 B1, B2,  , Bn 满足 1° B1, B2,  , Bn 两两互不相容， P(Bi)  0(i = 1,2,  ,n) ， 2°  n i A Bi =1  ， 则有 P(A) = P(B1)P(A | B1) + P(B2)P(A | B2) ++ P(Bn)P(A | Bn) 。 全概率公式解决的是多个原因造成的结果问题，全概率公式的题型：将试验 可看成分为两步做，如果要求第二步某事件的概率，就用全概率公式； （16）贝叶 斯公式 设事件 B1， B2 ，.， Bn 及 A 满足 1° B1， B2 ，.， Bn 两两互不相容， P(Bi) >0，i = 1，2，.， n ， 2°  n i A Bi =1  ， P(A)  0 ， 则 = = n j j j i i i P B P A B P B P A B P B A 1 ( ) ( / ) ( ) ( / ) ( / ) ，i=1，2，.n。 此公式即为贝叶斯公式。 ( ) P Bi ，（ i =1，2 ，.， n ），通常叫先验概率。 P(B / A) i ，（ i =1，2

),通常称为后验概率。贝叶斯公式反映了“因果”的概率规律，并作出了 “由果期因”的推断。将试验可看成分为两步做，如果求在第二步某事件发 生条件下第一步某事件的概率，就用贝叶斯公式。 我们作了1次试脸，且满足 每次试验只有两种可能结果，A发生或A不发生： n次试验是重复进行的，即A发生的概率每次均一样： ◆每次试验是独立的，即每次试验A发生与否与其他次试验A发生与 否是互不影响的。 (17)伯努这种试验称为伯努利概型，或称为n重伯努利试验。 利概型 用P表示每次试验A发生的概率，则A发生的概率为l-P=9,用P()表 示m重伯努利试验中A出现k(0≤k≤)次的概率。 P()=Chp'g"k=0,12,.,n。 1

1 n ），通常称为后验概率。贝叶斯公式反映了“因果”的概率规律，并作出了 “由果朔因”的推断。将试验可看成分为两步做，如果求在第二步某事件发 生条件下第一步某事件的概率，就用贝叶斯公式。 （17）伯努 利概型 我们作了 n 次试验，且满足 ◆ 每次试验只有两种可能结果， A 发生或 A 不发生； ◆ n 次试验是重复进行的，即 A 发生的概率每次均一样； ◆ 每次试验是独立的，即每次试验 A 发生与否与其他次试验 A 发生与 否是互不影响的。 这种试验称为伯努利概型，或称为 n 重伯努利试验。 用 p 表示每次试验 A 发生的概率，则 A 发生的概率为 1− p = q ，用 Pn(k) 表 示 n 重伯努利试验中 A 出现 k(0  k  n) 次的概率， k n k k n Pn k C p q − ( ) = ， k = 0,1,2,  ,n

第二章随机变量及其分布 (1)离散 设离散型随机变量X的可能取值为X(k=L,2,.)且取各个值的概率，即事 型随机变 的分布 k=1,2, 律 则称上式为离散型随机变量X的概率分布或分布律。有时也用分布列的形 式给出： X1X2.,XA., PX=x)pmp,.,p%,.。 显然分布律应满足下列条件： (1)p20,-1,2,. n- (2)连续 型随机变 设F)是随机变量X的分布函数，若存在非负函数八)，对任意实数x,有 量的分布 F(x)=["f(x)dx 密度 称X为连续型随机变量。称为X的摄率密度函数或密度函数，筒称 密度函数具有下面4个性质： 1、f(x)≥0。 2、 [f()ds=1 3.P(x<Xsx)=F()-F(x)=["f(x)d 4、P(=)=0,a为常数，连续型随机变量取个别值的概率为0 (3)离散 P(X=x)≈P(x<X≤x+d)≈f(x)dk 与连线刑 随机变 积分元∫x在连续型随机变量理论中所起的作用与P(X=x)=p:在离散 的关系 型随机变量理论中所起的作用相类似。 1

1 第二章 随机变量及其分布 （1）离散 型随机变 量的分布 律 设离散型随机变量 X 的可能取值为 Xk(k=1,2,.)且取各个值的概率，即事 件(X=Xk)的概率为 P(X=xk)=pk，k=1,2,.， 则称上式为离散型随机变量 X 的概率分布或分布律。有时也用分布列的形 式给出：     , , , , , , , , | ( ) 1 2 1 2 k k k p p p x x x P X x X = 。 显然分布律应满足下列条件： （1） pk  0 ， k = 1,2, ， （2）   = = 1 1 k pk 。 （2）连续 型随机变 量的分布 密度 设 F(x) 是随机变量 X 的分布函数，若存在非负函数 f (x) ，对任意实数 x ，有 − = x F(x) f (x)dx ， 则称 X 为连续型随机变量。 f (x) 称为 X 的概率密度函数或密度函数，简称概 率密度。 密度函数具有下面 4 个性质： 1、 f (x)  0。 2、  + − f (x)dx =1 。 3、 2 1 P( ) ( ) ( ) ( ) 1 2 2 1 x x x X x F x F x f x dx   = − =  4、P(x=a)=0,a 为常数，连续型随机变量取个别值的概率为 0 （3）离散 与连续型 随机变量 的关系 P(X = x)  P(x  X  x + dx)  f (x)dx 积分元 f (x)dx 在连续型随机变量理论中所起的作用与 P(X = xk ) = pk 在离散 型随机变量理论中所起的作用相类似

(4)分布 设X为随机变量，x是任意实数，则函数 函数 F(x)=PX≤x) 称为随机变量X的分布函数，本质上是一个累积函数。 P(a<X≤b)=F(b)-F(a)可以得到X落入区间(a,b]的概率。分布函 数F(x)表示随机变量落入区间(-四，x]内的概率。 分布函数具有如下性质： 1°0≤F(x)≤L,-0<x<+0: 2”F(x)是单调不减的函数，即I<x2时，有F(x)≤F(x): 3 F(-)=lim F(x)=0,F(+o)=lim F(x)=1; 4°F(x+O)=F(x),即F(x)是右连续的； 5°PX=x)=F(x)-F(x-0). 对于离数随机变品，F闭夏P,: 对于连续型随机变量，F(x)=「f(x)dk· (5)八大0-1分布P(《=)=p,PX0)= 分布 二项分布 在n重贝努里试验中，设事件A发生的概率为p。事件A发生的次 数是随机变量，设为X,则X可能取值为0,1,2，.，n P(X=k)=Pu(k)=Cip'q"- ， 中 q=1-p,0<p<1,k=0,l,2,n, 则称随机变量X服从参数为n,p的二项分布。记为X~B(nP) 当n=1时，P(X=)=pg,k=0.1,这就是(0-1)分布， 所以(01)分布是二项分布的特例。 1

1 （4）分布 函数 设 X 为随机变量， x 是任意实数，则函数 F(x) = P(X  x) 称为随机变量 X 的分布函数，本质上是一个累积函数。 P(a  X  b) = F(b) − F(a) 可以得到 X 落入区间 (a,b] 的概率。分布函 数 F(x) 表示随机变量落入区间（– ∞，x]内的概率。 分布函数具有如下性质： 1° 0  F(x)  1, −   x  + ； 2° F(x) 是单调不减的函数，即 x1  x2 时，有 F(x1)  F(x2) ； 3° (−) = lim ( ) = 0 →− F F x x ， (+) = lim ( ) = 1 →+ F F x x ； 4° F(x + 0) = F(x) ，即 F(x) 是右连续的； 5° P(X = x) = F(x) − F(x − 0) 。 对于离散型随机变量，   = x x k k F(x) p ； 对于连续型随机变量，  − = x F(x) f (x)dx 。 （5）八大 分布 0-1 分布 P(X=1)=p, P(X=0)=q 二项分布 在 n 重贝努里试验中，设事件 A 发生的概率为 p 。事件 A 发生的次 数是随机变量，设为 X ，则 X 可能取值为 0,1,2,  ,n 。 k k n k n P X k Pn k C p q − ( = ) = ( ) = ， 其 中 q = 1− p,0  p  1, k = 0,1,2,  ,n ， 则称随机变量 X 服从参数为 n ，p 的二项分布。记为 X ~ B(n, p) 。 当 n =1 时， k k P X k p q − = = 1 ( ) ，k = 0.1 ，这就是（0-1）分布， 所以（0-1）分布是二项分布的特例

泊松分布 设随机变量X的分布律为 x-若e,>0k=02 则称随机变量X服从参数为入的泊松分布，记为X~π()或者 p(2) 泊松分布为二项分布的极限分布(p=入，n一∞)。 几何分布 PX=k)=gp,k=1,2,3,其中p≥0，q=1-p 随机变量X服从参数为D的几何分布，记为G(D)。 均匀分布 设随机变量X的值只落在[a,b]内，其密度函数x)在[a,b]上 为常数 b-a' 即 〔1 a≤x≤b f(x)=b-a 0, 其他， 则称随机变量X在[a,b]上服从均匀分布，记为X-U(a,b)。 分布函数为 0, xb. 当a≤x<≤b时，X落在区间(，X2)内的概率为 P<X<)=- b-a 1

1 泊松分布 设随机变量 X 的分布律为  − = = e k P X k k ! ( ) ，  0， k = 0,1,2， 则称随机变量 X 服从参数为  的泊松分布，记为 X ~  () 或者 P(  )。 泊松分布为二项分布的极限分布（np=λ，n→∞）。 几何分布 P(X = k) = q k−1 p,k =1,2,3,  ，其中 p≥0，q=1-p。 随机变量 X 服从参数为 p 的几何分布，记为 G(p)。 均匀分布 设随机变量 X 的值只落在[a，b]内，其密度函数 f (x) 在[a，b]上 为常数 b − a 1 ，即      = − 0, , 1 f (x) b a 其他， 则称随机变量 X 在[a，b]上服从均匀分布，记为 X~U(a，b)。 分布函数为 − = = x F(x) f (x)dx 当 a≤x1b。 a≤x≤b

指数分布 che, x≥0 x0，则称随机变量X服从参数为入的指数分布。 X的分布函数为 「1-e-a F(x)0, x20 x<0。 记住积分公式： 「xedk=m 1

1 指数分布 其中   0 ，则称随机变量 X 服从参数为  的指数分布。 X 的分布函数为 记住积分公式： ! 0 x e dx n n x =  + − f (x) = , x e   − x  0, 0, x  0, F(x) = 1 , x e − − x  0, 0, x<0

正态分布 设随机变量X的密度函数为 f(x)=- 1 -00为常数，则称随机变量X服从参数为“、0的 正态分布或高新(Gaus)分布，记为X~N(4)。 f)具有如下性质： 1°x)的图形是关于x=“对称的： 当味。大 若X~N(G),则X的分布函数为 rw如e可 参数4=0、。=1时的正态分布称为标准正态分布，记为 X-N0,1其装瘦函数记为 p=J2元 ，-4)=a。 (7)函数离散型 已知X的分布列为 的分布函 X,x2.,. ,不 g(g(x8x· P(Y=y,) 若有某些g箱等，则应将对锅p,相加作为g的概率

1 正态分布 设随机变量 X 的密度函数为 2 2 2 ( ) 2 1 ( )    − − = x f x e ， −   x  +， 其中  、  0 为常数，则称随机变量 X 服从参数为  、 的 正态分布或高斯（Gauss）分布，记为 ~ ( , ) 2 X N   。 f (x) 具有如下性质： 1° f (x) 的图形是关于 x =  对称的； 2° 当 x =  时，   2 1 f ( ) = 为最大值； 若 ~ ( , ) 2 X N   ，则 X 的分布函数为 参数  = 0 、  =1 时的正态分 布称为 标准正态 分布， 记为 X ~ N(0,1) ，其密度函数记为 2 2 2 1 ( ) x x e − =   ， −   x  +， 分布函数为  − −  = x t x e dt 2 2 2 1 ( )  。 (x) 是不可求积函数，其函数值，已编制成表可供查用。 Φ(-x)＝1-Φ(x)且 Φ(0)＝ 2 1 。 如果 X ~ ( , ) 2 N   ，则  X −  ~ N(0,1) 。       −  −       −   =     2  1 1 2 ( ) x x P x X x 。 （6）分位 数 下分位表： P(X    )＝ ； 上分位表： P(X    )＝ 。 （7）函数 的分布函 数 离散型 已知 X 的分布列为     , , , , , , , , ( ) 1 2 1 2 n n i p p p x x x P X x X = ， Y = g(X ) 的分布列（ ( ) i i y = g x 互不相等）如下：     , , , , ( ), ( ), , ( ), ( ) 1 2 1 2 n n i p p p g x g x g x P Y y Y = ， 若有某些 g(xi) 相等，则应将对应的 i p 相加作为 g(xi) 的概率。 F x e dt x t −  − − = 2 2 2 ( ) 2 1 ( )   

连续型 F,)=P≤y}=Pg(x)s}=∫fx(x) 果代离股做复物度前数之间的 先利用X的概率密度￡，()写出Y的分布函数R(y)=P(g0≤y) 再利用变上下限积分的求导公式求出)。 (2)定理法： 当Y=g(X严格单调并且可导时： ④0)=IIha<y<a 0, 其它 其中h'y是gs)的反函数 1

1 连续型 先利用 X 的概率密度 fX(x)写出 Y 的分布函数 FY(y)＝P(g(X)≤y)， 再利用变上下限积分的求导公式求出 fY(y)。 （2）定理法： 当 Y=g(X)严格单调并且可导时: 其中 h’(y)是 g(x)的反函数