《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.1 复积分概述

第一节复变函数积分 一、复积分的定义 二、复积分的性质 三、复积分的计算
第一节复变函数积分 一、复积分的定义 二、复积分的性质 三、复积分的计算

1.关于曲线方向的说明: 一般:曲线C的正方向总是指从起,点到终点 的方向,那么终点到起点的方向就是曲线C的 负向,记为C 2.闭曲线正向的定义: C-一闭曲线正方向观察者顺此方向沿前进 一周的内部一直在观察者的左边。与之相 反的方向就是曲线的负方向
一般: 曲线C的正方向总是指从起点到终点 的方向.那么终点到起点的方向就是曲线C的 负向,记为C- C−−闭曲线正方向观察者顺此方向沿前进 一周的内部一直在观察者的左边。与之相 反的方向就是曲线的负方向. 2.闭曲线正向的定义: 1.关于曲线方向的说明: 2

.复变函数积分的定义 1.积分的定义: 设有有向曲线C:z=z(t)(a≤t≤B) 起点:M=z(),终,点:b=z(B),f(z)在C上有定义 (1)对C作分割T 把曲线C沿着从起点到终点的方向 任意分成n个孤段,设分,点依次为: 0=乙0,乙1,.,乙k-1,乙k,.,乙n=b, 3k1 (2)取,点 00312 0 在每个孤段乙k-1不k(k=1,2,.,)上任意取一点Sk
1.积分的定义: : ( ) ( ) ( ), ( ), ( ) C z z t t a z b z f z C 设有有向曲线 起点: 终点: 在 上有定义 o x y a b n1 z k z k1 z 2 z 1z k C 1 2 1 ( 1, 2, , ) , k k k z z k n 在每个弧段 上任意取一点 一. 复变函数积分的定义 0 1 1 , , , , , , , , k k n C n a z z z z z b 把曲线 沿着从起点到终点的方向 任意分成 个弧段 设分点依次为: (1) 对C作分割T (2)取点 0 a z n bz 3

③)作(Rinmann)和 S.=官f6,&,-)=25.aw 这里△k=乙k-乙k-1,△Sk=乙k-2的长度, 记6(=TD=max{As}, l≤k≤n (4)求极限 当n无限增加且6→0时, 91 k-1 如果不论对C的分法及Sk的 0 X 取法如何,Sn有唯一有限的极限J,则称f(z)沿着C的正 向可积,极限值J称为函数∫(z)沿曲线C的积分,记为 Jf(z)dz
1 1 1 ( ) ( ) ( ) , n n n k k k k k k k S f z z f z o x y A B n1 z k z k1 z 2 z 1z k C 1 2 1 ( ) max{ }, k k n T s 记 , , 这里 zk zk zk1 sk zk1zk的长度 ( 当n无限增加且 0时, , ( ) ( ) , , C k n J f z S J C f z C 如 极限值 称为函数 果不论对 的分法及 的 取法如何 有 有 沿曲线 唯一 限的极限 则称 沿 的积分 着 的 向可积, 记为 正 (3)作(Rinmann)和 (4)求极限 ( )d C f z z 4

复变函数 即:厂cfa)k=im∑f5)△z: 8→0 k=1 关于定义的说明: ()用。f(z)dz表示f(2)沿着曲线C的负向的积分 (2)f(z)沿着此闭曲线C的积分也可以记为∮f(z)k。 (3)如果C是x轴上的区间a≤x≤b,而f(z)=(x), 这个积分定义就是一元实变函数积分的定义 一般不能把∫f(a)dz写成∫”f(z)dk形式 (4) 因为:一般f(z)z的值不仅与起点,终点b有关, 更与积分路线C有关
关于定义的说明: (3) , ( ) ( ), . 如果 C 是 x 轴上的区间a x b 而 f z u x 这个积分定义就是一元实变函数积分的定义 0 1 : ( ) lim ( ) . n n k k C k f z dz f z 即 (1) ( )d ( ) C f z z f z 用 表示 沿着曲线C的负向的积分 (4) ( )d ( ) b C a f z z f z dz 一般不能把 写成 形式 ( , C )d C f z z a b 因为 :一般 的值不仅与起 更与积分路 点 终点 有关, 线 有关 (2) f (z) C f (z)dz. C 沿着此闭曲线 的积分也可以记为 5

复积分的性质 复积分与实变函数的定积分有类似的性质。 (④cfa)dz=-cfz)dz (2)f(z)dz=kf(a)d;(k为常数) (3)jcfa)±galz=cfad±cgz)dz: 被积函数的线性可加性
二、复积分的性质 复积分与实变函数的定积分有类似的性质. (1) ( )d ( )d ; C C f z z f z z (2) kf (z)dz k f (z)dz; (k为常数) C C (3) [ ( ) ( )]d ( )d ( )d ; C C C f z g z z f z z g z z 被积函数的线性可加性 6

(4)设:C=C+C+C+.+C f()d =Sf()d+ff()++f()dz. 积分路径的可加性 (5)f(d(ds [dz=(dx)2+(dy)2 ds (6)若在C上有f(z)≤M,C的长记为L,则上式可 成为f(zykML
积分路径的可加性 (5) ( )d ( ) d ( ) ds C C C f z z f z z f z 2 2 dz (dx) (dy) ds 1 2 3 (4) 设 C C C C Cn : C f (z)dz ( )d ( )d ( )d . 1 2 C C Cn f z z f z z f z z f z dz ML C f z M C L C ( ) (6) ( ) 成为 若在 上有 , 的长记为 ,则上式可 7

二、发刀于工门余干义异屏 1.充分条件 定理3.1设函数f(z)=u(x,y)+iw(x,y)在光滑曲线C上 连续,则复积分∫f(z存在,而且可以表示为 [f(= =uxx,+(xy少+ax, 这是实的第二型曲线积分
三、复 积分存在的条件及计算 1. 充分条件 连续 则复积分 存在 而且可以表示为 定理 设函数 在光滑曲线 上 , ( ) , 3.1 ( ) ( , ) ( , ) f z dz f z u x y iv x y C C f z dz C ( ) u x y dx v x y dy i v x y dx u x y dy C C ( , ) ( , ) ( , ) ( , ) 这是实的第二型曲线积分
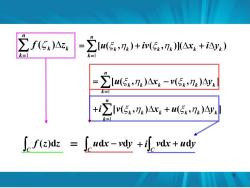
∑f5)s -lu)+iv)x,+i) k= 2M5,)Ax-W57.)y +i∑Iv(5,nk)△xx+(5,nk)Ay ke Sf()dz =fudx-vdy+ivdx+udy
1 1 [ ( , ) ( , ) ] [ ( , ) ( , ) ] n k k k k k k k n k k k k k k k u x v y i v x u y C f (z)dz C udx vdy C i vdx udy 1 ( ) n k k k f z 1 [ ( , ) ( , )]( ) n k k k k k k k u iv x iy 9

关于定理的几,点说明: ()当f()在光滑曲线C上是连续函数时,积分「f(z) 一定存在 (2)积分「f(2)河以通过两个二元实变函数的线积分 来计算 (3)设C:z(t)=x(t)+y(t),a≤t≤b,则有 ∫cfzk=∫(dt. 复积分计算的参数方程法 10
关于定理的几点说明: . (1) ( ) C , ( ) 一定存在 当 在光滑曲线 上是连续函数时 积分C f z f z . (2) ( ) 来计算 积分 可以通过两个二元实变函数的线积分 C f z (3)设C:z(t) x(t) iy(t),a t b,则有 ( ) [ ( )] ( )d . b C a f z dz f z t z t t 10 复积分计算的参数方程法
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.2 柯西积分定理.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.3 柯西积分公式.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第三章 复变函数的积分 3.4 高阶导数公式.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.1 解析函数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.2 解析函数与调和函数的关系.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第二章 解析函数 2.3 复变初等函数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.1 复数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.2 复数的表示.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.3 平面点集.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.4 无穷大.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第一章 复数与复变函数 1.5 复变函数的概念.ppt
- 《高等数学》课程教学资源(单元测验)第1-7章单元测验(附答案).doc
- 《概率论与数理统计》课程教学资源(知识点与公式)概率论与数理统计公式全集.doc
- 《概率论与数理统计》课程教学资源(知识点与公式)概率论与数理统计概率部分知识点总结.doc
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第一节 假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第二节 正态总体均值的假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第三节 正态总体方差的假设检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第8章 假设检验 第六节 分布拟合检验.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第一节 点估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第7章 参数估计 第三节估计量的评选标准.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.4 解析函数的洛朗展开.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.3 解析函数的泰勒展开.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.2 幂级数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第四章 解析函数的级数表示 4.1 复数项级数.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.4 对数留数与辐角原理.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.3 留数在积分计算中的应用.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.2 留数及留数定理.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第五章 留数及其应用 5.1 孤立奇点.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第六章 共形映射 6.4 分式线性变换的构造.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第六章 共形映射 6.3 分式线性变换的性质.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第六章 共形映射 6.2 共形映射的基本问题.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第六章 共形映射 6.1 共形映射.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第七章 傅里叶变换 7.3 傅里叶变换的性质.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第七章 傅里叶变换 7.2 脉冲函数及其傅里叶变换.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第七章 傅里叶变换 7.1 傅里叶变换.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第八章 拉普拉斯变换 8.4 拉普拉斯变换的应用.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第八章 拉普拉斯变换 8.3 拉普拉斯逆变换.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第八章 拉普拉斯变换 8.2 拉普拉斯变换性质.ppt
- 《复变函数与积分变换》课程教学课件(PPT讲稿)第八章 拉普拉斯变换 8.1 拉普拉斯变换的概念.ppt
- 《线性代数》课程教学课件(PPT讲稿)第一章 行列式 1.4 克拉默法则.ppt
