《复变函数与积分变换》课程教学课件（PPT讲稿）第六章 共形映射 6.2 共形映射的基本问题

第二节共形映射的基本问题 一、基本问题 (I)对于给定的区域D和定义在D上的解析函数w= f(z),求像集，G并讨论函数是否将D共形映射为G, (2)对于给定的区域D和区域G,求一个解析函数 w=f(z),使得函数f(z)将区域D共形映射为G. 对于问题1)，我们有如下的定理： 二、解析函数的保域性定理和边界对应原理

第二节 共形映射的基本问题 1 ( ), , . (1) f z G D G D D w 求像集 并讨论函数是否将 共形映射为 对于给定的区域 和定义在 上的解析函数 = ( ), ( ) . (2) , w f z f z D G D G 使得函数 将区域 共形映射为 对于给定的区域 和区域 求一个解析函数 = 对于问题(1)，我们有如下的定理: 二、解析函数的保域性定理和边界对应原理 一、基本问题

定理6.2（保域性定理）设函数在区域D解析，并且不 恒为常数，则像集G=f(D)是区域 定理6.3（边界对应原理） 设区域D的边界为简单闭曲线C,函数w=f(z)在D 上解析，且将C双方单值的映射成简单闭曲线厂，当 z沿C的正向绕行时，相应w的绕行方向定义为Γ的 正向，并令G是以Γ为边界的区域，则w=f(z)将D共 形映射为G, 回 2

2 , ( ) . 6.2( ) , 恒为常数 则像集 是区域 定理 保域性定理 设函数在区域 解析 并且不 G f D D = 定理6.3(边界对应原理) . , , ( ) , , , , ( ) G G w f z D z C w C D C w f z D 形映射为 正向 并令 是以 为边界的区域 则 将 共 沿 的正向绕行时 相应 的绕行方向定义为 的 上解析 且将 双方单值的映射成简单闭曲线 当 设区域 的边界为简单闭曲线 函数 在  =   =

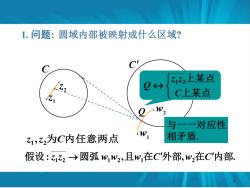
1.问题：圆域内部被映射成什么区域？ 上某点 C上某点 W2 与 一一对应性 乙1，乙2为C内任意两点 相矛盾. 假设：z1乙2→圆弧w,w2,且w,在C外部2在C'内部

1. 问题: 圆域内部被映射成什么区域? C C . . , z1 z2为C内任意两点 1 .z 2 z . w1 w2 . . . Q : , , . 假设 z1 z2 →圆弧 w1w2 且w1在C外部 w2在C内部     上某点 上某点 C z z Q 1 2 与一一对应性 相矛盾. 3

结论：在共形映射下，C的内部不是映射成 C的内部便映射成C'的外部 判别方法： 方法1在共形映射下，如果在圆周C内任取 一点z,若z的象在C'内部，则C的内部就映为 C'的内部若z的象在C外部，则C的内部就映 为C的外部

结论: 在共形映射下, C的内部不是映射成 C的内部便映射成C的外部. 判别方法: 方法1 在共形映射下, 如果在圆周C内任取 , 0 一点z 为C的外部. C的内部; , 若 z0的象在C内部 则C的内部就映为 , 若 z0的象在C外部 则C的内部就映 4

方法2 在C上取三点乙1，乙2，乙3，若绕向： 乙1→2>3，与C上绕向%1→w2→w3相同， 则C的内部就映为C的内部. 13 w3 Z1 12

方法2 , , , : 在C上取三点z1 z2 z3 若绕向 , . z1 → z2 → z3 与C 上绕向w1 → w2 → w3 相同 w3 . w1 . w2 . C C 1 z . 2 z . . 3 z 则C的内部就映为C的内部. 5

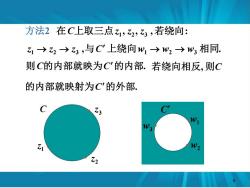
方法2在C上取三点1，乙2，乙3，若绕向： 乙1→2→乙3，与C上绕向%，→w2→w3相同. 则C的内部就映为C的内部.若绕向相反，则C 的内部就映射为C的外部， 13 W3 1 W2 12 6

C C w2 . w1 . w3 . 1 z . 2 z . . 3 z 若绕向相反, 则C 方法2 , , , : 在C上取三点z1 z2 z3 若绕向 , . z1 → z2 → z3 与C 上绕向w1 → w2 → w3 相同 则C的内部就映为C的内部. 的内部就映射为C的外部. 6

三、共形映射的存在性和唯一性 1、关于存在性当区域为下列两种情它一时， 均不存在解析函数使之保形的映射为单圆 内部. (区域是扩充复平面 (2)区域是扩充复平面除去一点 2、关于惟一性，一般说来是不惟一的 3、定理6.4（黎曼存在唯一性定理）

内部. 均不存在解析函数,使之保形的映射为单位圆 1、关于存在性,当区域为下列两种情况之一时, (1)区域是扩充复平面 (2)区域是扩充复平面除去一点 2、关于惟一性,一般说来是不惟一的. 7 三、共形映射的存在性和唯一性 3、定理6.4(黎曼存在唯一性定理)

设D与G是任意给定的两个单通区域，它们的边 界至少包含两点则必存在解析函数v=f(z),把D 保形的映射为G,如果在D和G内再分别任意指定 一点z0,w,并任给一个实数π≤日。≤π，要求函数 w=f(z)满足w。=f(zo),且argf'(zo)=0,则映射 w=f(z)是惟一的. (1)定理仅肯定了满足给定条件函数的存在唯一性. (2)定理条件是函数的存在唯一性的充分条件不是 必要的.(3)定理没给出具体的求解方法

保形的映射为G, 界至少包含两点,则 存在解析函数 把 D 设 与 是任意给定的两个单连通区域,它们的边 w f (z), D G 必 = 8 是惟一的. 满 足 且 则映射 一 点 并任给一个实数 要求函数 ( ) ( ) ( ), arg ( ) , , , 0 0 ' 0 0 0 0 0 w f z w f z w f z f z z w = = = = −       如果在D和G内再分别任意指定 (1)定理仅肯定了满足给定条件函数的存在唯一性. (2)定理条件是函数的存在唯一性的充分条件不是 必要的. (3)定理没给出具体的求解方法