《线性代数》课程教学课件（PPT讲稿）第三章 矩阵的运算 3-4 分块矩阵

§3.4分块矩阵 一、分块矩阵的概念 二、分块矩阵的运算 三、矩阵乘法的几种分块方法 四、分块对角矩阵

§3.4 分块矩阵 一、分块矩阵的概念 二、分块矩阵的运算 三、矩阵乘法的几种分块方法 四、分块对角矩阵

一、分块矩阵的概念 1.定义设A是一个矩阵，在A的行和列之间加上一些 横线和竖线，把矩阵A分成若干小块，用这种方法得 到的形式矩阵称为一个分块矩阵 例如 414:415 421422:23 24L25 A= 431 32 : l33 3435 4142L43 4445」 则A可记为 A A12 A An

31 32 3 11 3 13 14 23 24 1 41 42 5 25 34 43 4 12 2 35 1 4 5 22 4 a a a a a a a a a a a a a a a a a a a A a       =       21 1 12 3 1 2 2 13 A 2 A A A A A   A =     一、分块矩阵的概念 . , , 1. , 到的形式矩阵称为一个分块矩阵 横线和竖线 把矩阵 分成若干小块 用这种方法得 定义设 是一个矩阵 在 的行和列之间加上一些 A A A 例如则A可记为

例如 2 3 1 2 3 4 5 6 8 56 7 8 一4 -3 -2 -1 -4 -3 -2-1 -8 -7 -6 -5 -8-7 -6-5 上述分块后则不是分块矩阵 关于分块矩阵的说明： 1分块后，每行子块的行数相同，每列子块的列数相 同.（添加的横线和竖线贯穿矩阵的上下，左右）

1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 关于分块矩阵的说明: .( , .) 1. , , 同 添加的横线和竖线贯穿矩阵的上下 左右 分块后 每行子块的行数相同 每列子块的列数相 上述分块后则不是分块矩阵. 例如

2.对于一个矩阵，由于横线和纵线的取法不同，得到 的分块矩阵也不同 3矩阵在分块时，只有当行的分块和列的分块都确 定后，分块矩阵才唯一确定 分块矩阵运算遵循原则： 4.在进行分块矩阵运算时，要保证分块前后都要可 以运算，同时运算结果要相同 5.在进行分块矩阵运算时，只需要将子块当成数去 处理，运算规律按矩阵相应运算进行

. 2. , , 的分块矩阵也不同 对于一个矩阵 由于横线和纵线的取法不同 得到 , . 3. , 定后 分块矩阵才唯一确定 矩阵在分块时 只有当行的分块和列的分块都确 , . 4. , 以运算 同时运算结果要相同 在进行分块矩阵运算时 要保证分块前后都要可 , . 5. , 处理 运算规律按矩阵相应运算进行 在进行分块矩阵运算时 只需要将子块当成数去 分块矩阵运算遵循原则:

2.特殊分法 设矩阵A=(a)xn, 按行分块A= A. 其中A:=(a,2,.,4n)》 4,] i=1,2,.,S. 按列分块A=（A,A,.,An),其中A= azj j=1,2,.,n

2.特殊分法 设矩阵 ( ) , A a = ij s n 按列分块 A A A A = ( 1 2 , , , n ) ，其中 1 2 , j j j nj a a A a       =         j n = 1,2, , . 按行分块 1 2 , s A A A A     =         其中 1 2 ( , , , ), A a a a i i i in = i s = 1,2, ,

矩阵的行列都要分，且分到最细时得到 11 12 u21 22 。 : Aml 此时，分块矩阵就是前面的矩阵，于是可以说 分块矩阵是矩阵的形式推广，矩阵是分块矩阵的一 种特殊情况

              m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 矩阵的行列都要分,且分到最细时得到 此时,分块矩阵就是前面的矩阵,于是可以说 . , 种特殊情况 分块矩阵是矩阵的形式推广 矩阵是分块矩阵的一

二、分块矩阵的运算 1、加法 设A,B是两个m×n矩阵，对它们用 同样的分法分块： A= B= Ap B q 其中子块A,与B为同型矩阵，则 Au+Bu A十B= Ap1+Bp1.Apg+B」

11 1 11 1 1 1 , q q p pq p pq A A B B A B A A B B         = =             1、加法 设 A, B 是两个m×n 矩阵，对它们用 同样的分法分块: 二、分块矩阵的运算 11 11 1 1 1 1 . q q p p pq pq A B A B A B A B A B   + +   + =     + +   其中子块 Aij 与 Bij 为同型矩阵，则

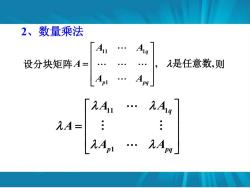
2、数量乘法 A 设分块矩阵A= 2是任意数，则 九A=

2、数量乘法 设分块矩阵 11 1 1 , , q p pq A A A A A      =       是任意数 则 11 1 1 q p pq A A A A A          =      

3、乘法把矩阵A=(ak)mxs,B=(bg)xp分块成 其中A1,A2,.,A的列数分别等于B,B2j,., B的行数，那末 四浪A 其中Cg=∑4xB6(i=1,pj=1,）

11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B         = =             其中 的列数分别等于 的行数 那末 ( ) 11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q =     =       其中 = = =  3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m s kj s p   分块成

说明： 1.当左边分块矩阵的列的分块方法和右边分块矩阵的分 块方法相同时，两个分块矩阵才可以相乘 2.两个分块矩阵的乘积仍是分块矩阵，并且乘积分块矩 阵的行数等于左边分块矩阵的行数，乘积分块矩阵的列 数等于右边分块矩阵的列数 3.分块矩阵的第行第列子块C等于左边分块矩阵的第 行与右边分块矩阵第列的对应子块乘积之和 Ci=AnBy++Aip Bp

Ci j = Ai1 B1 j ++ Ai pBp j 说明: , . 1. 块方法相同时 两个分块矩阵才可以相乘 当左边分块矩阵的列的分块方法和右边分块矩阵的分 . , 2. , 数等于右边分块矩阵的列数 阵的行数等于左边分块矩阵的行数 乘积分块矩阵的列 两个分块矩阵的乘积仍是分块矩阵 并且乘积分块矩 . 3. 行与右边分块矩阵第 列的对应子块乘积之和 分块矩阵的第 行第 列子块 等于左边分块矩阵的第 i j i j Ci j