《复变函数与积分变换》课程教学课件（PPT讲稿）第六章 共形映射 6.3 分式线性变换的性质

第三节分式线性映射 一、分式线性映射的定义 二、几种简单的分式线性映射 三、分式线性映射的性质

第三节分式线性映射 一、分式线性映射的定义 二、几种简单的分式线性映射 三、分式线性映射的性质

一、 分式线性映射的定义 w= az b (ad-bc≠0，a,b,c,d均为常数) cz d 称为分式线性映射， 说明： 1)ad-bc≠0的限制，保证了映射的保角性. dw ad-bc 否则，由于d(红+=0，有w=常数 那末整个z平面映射成w平面上的一点

(ad bc 0, a,b,c,d均为常数.) cz d az b w −  + + = 称为分式线性映射. 说明: 否则, 由于 0, . d ( ) d 2 = 有  常数 + − = w cz d ad bc z w 那末整个z平面映射成 w平面上的一点. 1) ad − bc  0的限制，保证了映射的保角性. 2 一、分式线性映射的定义

2)由w=+b (ad-bc≠0) c+d dw+b d-bc≠0 cw-a 分式线性映射的逆映射，也是分式线性映射. 3)两分式线性映射w= as+B 5+68 (aδ-By≠0) 5 收+日(a6-By≠0)复合仍为分式线性映 az+B 射w= az+b ad-bc=(a6-By)(a'6'-B'y')≠0) cz +d

分式线性映射的逆映射, 也是分式线性映射. 2) 由 ( −  0) + + = ad bc cz d az b w ( −  0) − − + = ad bc cw a dw b z 3) 两分式线性映射 ( −  0) + + =        w (   −    0)  +   +  =          z z 复合仍为分式线性映 (( − = ( − )(   −  )  0)) + + = ad bc        cz d az b 射 w 3

4)分式线性映射 az+b be-ad W= =0+ cz+d c c(cz+d) 8=e+山，则w=A52+B(AB为微数 一个一般形式的分式线性映射是由下列四种 特殊的简单映射复合而成： (w=z+b,(2)w=ze,(3)w=1z,(④w= 对w= aztb 的研究可化为对以上谢的研究 cz +d

4) 分式线性映射 c(cz d) bc ad c a cz d az b w + − = + + + = , 1 , 1 1 2  令 = cz + d  = ( , ) 则w = A 2 + B A B为常数 一个一般形式的分式线性映射是由下列四种 特殊的简单映射复合而成: (1) w = z + b, (2) , i w = z e (3) w = rz, . 1 (4) z w = 对 的研究可化为对以上映射的研究. cz d az b w + + =

例6.5将分式映射w= 2 分解为四种形式的复合. z+i 解： 2z -2i W=- =2+ =2+2e z+i z+i → 2→42→w 由于前三种函数可以构成整式线性映射，因此分式 线性映射可以分解为整式线性映射与w=1的复合 Z

例6.5将分式映射 分解为四种形式的复合. z iz w + = 2 解： ) 1 2 2 ( 2 2 2 2 z i e z ii z iz w i + = + +− = + + = − z z z z z w z i z z e z z i ⎯⎯→ ⎯⎯→ ⎯⎯⎯→ ⎯⎯→ ⎯ ⎯→ + + − 2 4 2 2 3 1 1 3 4 2 1 2  线性映射可以分解为整式线性映射与 的复合. 由于前三种函数可以构成整式线性映射,因此分式 z w 1 = 5

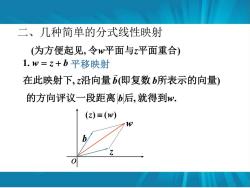
二、几种简单的分式线性映射 (为方便起见，令w平面与z平面重合) 1.w=z+b平移映射 在此映射下，z沿向量（即复数b所表示的向量） 的方向评议一段距离b后，就得到w. (z)≡(w)

二、几种简单的分式线性映射 1. w = z + b 平移映射 (为方便起见, 令w平面与z平面重合) 在此映射下, z沿向量b(即复数b所表示的向量)  的方向评议一段距离 b后,就得到w. o (z)  (w) z b w 6

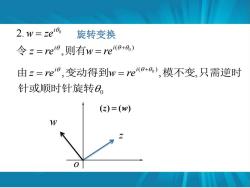
2.w=ze8, 旋转变换 令z=re,则有w=re0+8) 由z=re0,变动得到w=re(a+a),模不变，只需逆时 针或顺时针旋转8， (z)=(w)

0 2. i w = ze 旋转变换 ( ) 0 ,   + = = i i 令 z re 则有w re o (z) = (w) z w 0 ( ) , , , 0     针或顺时针旋转 由z = re i 变动得到w = re i + 模不变 只需逆时

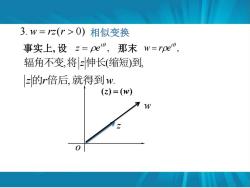
3.w=z(r>0)相似变换 事实上，设z=pe,那末w=rpe0, 辐角不变，将z伸长（缩短）到， z的r倍后，就得到w: (Z)=(w)

3. w = rz(r  0) 相似变换 事实上, 设 ,   i z = e 那末 ,   i w = r e 辐角不变,将 z伸长(缩短)到, z的r倍后,就得到w. o (z) = (w) 8 z w

4.w=- 反演映射 此映射可进一步分解为 1 W1= w=W 欲由点z作出点w,可考虑如下作图次序： →7→ 关于横轴对称 关键：在几何上如何由z→w,?

关于横轴对称 z w 1 4. = 反演映射 此映射可进一步分解为 , 1 1 z w = w = w1 欲由点z作出点w, 可考虑如下作图次序: z → z → w1 → w 关键: 在几何上如何由z → w1 ? 9

对称点的定义： 设C为以原点为中心，r为半径的圆周.在以 圆心为起点的一条半直线上，如果有两点P与P 满足关系式 0P.0p'=r2, 那末就称这两点为关于这圆周的对称点. 规定：无穷远点的对称点是圆心O

对称点的定义: 设C为以原点为中心, r为半径的圆周. 在以 圆心为起点的一条半直线上,如果有两点P与P 满足关系式 , 2 OP OP = r 那末就称这两点为关于这圆周的对称点. 规定: 无穷远点的对称点是圆心O. 10