《线性代数》课程教学课件（PPT讲稿）第一章 行列式 1.2 行列式的性质

§1.2行列式的性质 一、行列式的性质 二、应用举例 三、小结思考题

§1.2 行列式的性质 一、行列式的性质 二、应用举例 三、小结 思考题

一、 行列式的性质 利用行列式的定义计算特殊类型的行列式比较 简单，但对一般的行列式，特别是高阶行列式，计 算量相当大为简化行列式的计算，下面我们来讨 论行列式的性质.首先介绍一个重要的定理. 由上节n阶行列式的定义式可知，n阶行列式可 表示为第一行的元素与其对应的代数余子式的乘积 之和，因此，行列式按第一行的展开式，事实上， 行列式可按任意一行（列)展开

一、行列式的性质 利用行列式的定义计算特殊类型的行列式比较 简单，但对一般的行列式，特别是高阶行列式，计 算量相当大.为简化行列式的计算，下面我们来讨 论行列式的性质.首先介绍一个重要的定理. 由上节n阶行列式的定义式可知，n阶行列式可 表示为第一行的元素与其对应的代数余子式的乘积 之和，因此，行列式按第一行的展开式，事实上， 行列式可按任意一行（列）展开

定理1.2.1n阶行列式等于它的任意一行（列）的元素 与其对应的代数余子式的乘积之和，即 D=a1A1+2A2+.+anAn(i=1,2,.,n） 或 D=41yAy+42jA2j+.+4wAn(j=1,2,.,n) 推论如果n阶行列式中的行所有元素除，外都为 零，那么行列式就等于与其对应的代数余子式 的乘积，即 D=ajAi

定理1.2.1 n阶行列式等于它的任意一行(列)的元素 与其对应的代数余子式的乘积之和，即 1 1 2 2 . ( 1,2, , ) D a A a A a A i n = + + + = i i i i in in 1 1 2 2 . ( 1,2, , ) D a A a A a A j n = + + + = j j j j nj nj 或 ij a ij 零，那么行列式就等于 a 推论 如果n阶行列式中的i行所有元素除 外都为 与其对应的代数余子式 的乘积，即 D a A = ij ij

设n阶行列式 11 12 D- M21 422 : An2 .m 若把D中每一行元素换成同序数的列元素，则的新 行列式 21 D'= 12 L22 2 1nL2n·0m 行列式D'(或D')称为行列式D的转置行列式

设n阶行列式 nn a a a  22 11    n n a a a 2 12 1   1 2 21 n n a a a D =    2 21 1 n n a a a   n n a a a 1 2 D 12  = nn a a a  22 11 若把D中每一行元素换成同序数的列元素，则的新 行列式 ( ) . T 行列式D D D  或 称为行列式 的转置行列式

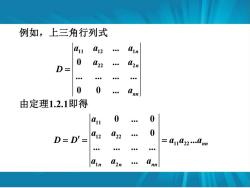
例如，上三角行列式 l11 412 n 0 D= 2 0 0 由定理1.2.1即得 0 0 0 D=D'= 012 22 = L11L22.0m 00e ain A2n

例如，上三角行列式 11 12 1 22 2 . 0 . . . . . 0 0 . n n nn a a a a a D a = 11 12 22 11 22 1 2 0 . 0 . 0 . . . . . . nn n n nn a a a D D a a a a a a = = =  由定理1.2.1即得

性质1行列式与它的转置行列式相等 证： 当n=2时， 011412 121 ,结论成立 21022 12L22 假设对n-1阶行列式结论成立.对n阶行列式D和D', 分别按第一行和第一列展开，得 0-2M, 21 02j-1 L2j+1 ，2n -2a,-1 An\ L-1 Anj+1 Ann

性质1 行列式与它的转置行列式相等. 证： 11 12 11 21 21 22 12 22 a a a a a a a a 当n=2时， = ，结论成立. 1 1 1 21 2 1 2 1 2 1 1 1 1 1 1 ( 1) . . ( 1) . . . . . . . . n j j ij j j j n n j j j n nj nj nn D a M a a a a a a a a a + = − + + = − + = − = −   假设对n-1阶行列式结论成立.对n阶行列式D和 ， 分别按第一行和第一列展开，得 D

a21 . a . . . D-24-g-2a,-m 2j-1 . 0j-1 . -1 . Qj+1 Anj+1 . 2m 由于Mn和M是n-1阶行列式，且M是M,的转置 行列式，根据假设M,=M,于是D=D' 说明行列式中行与列具有同等的地位，因此行列式 的性质凡是对行成立的对列也同样成立

21 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1 1 2 . . . . . . . . . ( 1) ( 1) . . . . . . . . . i n n n j ij nj j j j ij j j j j ij nj n in nn a a a a a a D a M a a a a a a a − − − + + = = + + +   = − = −   Mij Mij  Mij M M ij ij =  Mij 由于 和 是n-1阶行列式，且  是 的转置 行列式，根据假设 ，于是 D D =  说明 行列式中行与列具有同等的地位,因此行列式 的性质凡是对行成立的对列也同样成立

性质2互换行列式的两行（列），行列式变号： 证：用数学归纳法， 当n=2时，42 02122 结论成立 02122 011012 假设对n-1阶行列式结论成立.对n阶行列式D 1 12 .ee .ee i 12 D- . asi as2 asn .ee an an2

证： 用数学归纳法. 11 12 21 22 21 22 11 12 a a a a a a a a 当n=2时， = − ，结论成立. 假设对n-1阶行列式结论成立.对n阶行列式D 性质2 互换行列式的两行(列),行列式变号. 11 12 1 1 2 ln 1 2 1 2 . . . . . . . . . . . . . . . . . . . . . . . n l l s s sn n n nn a a a a a a D a a a a a a =

互换D中的第s行和第行，得 12 as1 as2 D1= . a L12 an 0n2

互换D中的第s行和第l行，得 11 12 1 1 2 1 1 2 ln 1 2 . . . . . . . . . . . . . . . . . . . . . . . n s s sn l l n n nn a a a a a a D a a a a a a =

分别将D和D按第行展开i≠s,),得 D->a(-1YMg.D.-Eac(-1YNg i=1 i=1 其中Mn和N分别是D和D,中元素a,的余子式，并且 N是由M互换两行得到的n-1阶行列式，由归纳假 设M=-N因此D=-D· 通常以表示行列式的第行，以c,表示行列式的第列， 交换i,两行记作r;)r,而交换i,两列记作C,分C·

1 分别将D D i i s l 和 按第 行展开( , ),  得 1 1 1 ( 1) , ( 1) n n i j i j ij ij ij ij j j D a M D a N + + = = = − = −  1 1 - 1 . ij ij ij ij ij ij ij M N D D a N M n M N D D = − = − 其中 和 分别是 和 中元素 的余子式，并且 是由 互换两行得到的 阶行列式，由归纳假 设 ，因此 , . i i i j i j r i c i i j r r i j c c   通常以 表示行列式的第 行,以 表示行列式的第 列, 交换 ， 两行记作 而交换 ， 两列记作