《线性代数》课程教学课件（PPT讲稿）第四章 线性方程组 4-2 齐次线性方程组

§4.2齐次线性方程组 一、齐次线性方程组的性质 二、基础解系及其求法 三、小结

§4.2 齐次线性方程组 一、齐次线性方程组的性质 二、基础解系及其求法 三、小结

一、齐次线性方程组解的性质 设有齐次线性方程组 %1比1+012X2++01mXn=0 21x1+022X2+.+L2mXn=0 (4-5) ml七1+0m2X2++AmnXn=0 11 12 若记A= 21 L22 Q2n X2 ,X= (m2 n

设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （4-5） 一、齐次线性方程组解的性质 11 12 1 1 21 22 2 2 1 2 , n n m m mn n a a a x a a a x A x a a a x             = =            

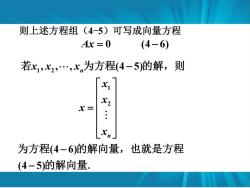
则上述方程组(4-5)可写成向量方程 Ax=0 (4-6) 若x1,x2,x,为方程(4-5)的解，则 2 x= n 为方程(4一6)的解向量，也就是方程 (4-5)的解向量

则上述方程组（4-5）可写成向量方程 Ax = − 0 (4 6) 1 2 1 2 , , , (4 5) (4 6) (4 5) n n x x x x x x x −       =       − − 若 为方程 的解，则 为方程 的解向量，也就是方程 的解向量

性质4.2.1两个解向量的和仍然是解向量，即 设5,5，是方程组(4-5)的解向量，则5+5也 是方程组(4-5)的解向量 证明只需证明5+52满足方程组(4-6)即可 .A51=0,A52=0 ∴.A(5+52)=A5+A52=0 故x=51+52也是Ac=0的解

1 2 1 2 , (4 5 4.2. ) (4 5 1 )     − + − 两个解向量的和仍然是解向量，即 设 是方程组 的解向量， 性质 则 也 是方程组 的解向量. 证明  A( 1 +  2 ) = A 1 + A 2 = 0  A 1 = 0, A 2 = 0 故 x 也是Ax 0的解. =  1 +  2 = 只需证明  1 2 + 满足方程组(4 6) − 即可

性质4.2.2一个解向量的倍数仍是解向量，即 设5是方程组(4-5)的解向量，是任意数， 则25也是方程组(4-5)的解向量. 证明：A(25)=元A(5)=0=0. ∴.25也是方程组(4-5)的解向量 由性质4.2.1、4.2.2知，齐次线性方程组(4-5)的 解向量的线性组合仍是(45)的解向量. 设51,52，.，5n-,是方程组(4-5)的解向量，1,2，.2n 是任意数，则2,5+入，52+.+元n-,5n,仍是方程组 (4-5)的解向量

(4 5) (4 5 . .2 ) 4 2     − − 一个解向量的倍数仍是解向量，即 设 是方程组 的解向量， 是任意数， 则 性质 也是方程组 的解向量. 证明 A A (    1 1 ) = = = ( ) 0 0.  − 也是方程组(4 5)的解向量 由性质4.2.1、4.2.2知，齐次线性方程组(4-5)的 解向量的线性组合仍是(4-5)的解向量 . 1 2 1 2 1 1 2 2 , , , (4 5) , , (4 5) n r n r n r n r             − − − −  −  + ++ − 设 是方程组 的解向量， 是任意数，则 仍是方程组 的解向量

二、基础解系及其求法 由于方程组(4-5)的所有解，对于加法和数乘运算构 一个向量空间，也称为方程组(4-5)解空间. 下面我们来求解空间的一个最大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A 的前个列向量线性无关，于是A的行最简形为 1 0b1r+1 bin 0 1 b I= r+l b 0 0 0 0 0 。 0 0 0

二、基础解系及其求法 由于方程组(4-5)的所有解,对于加法和数乘运算构 一个向量空间,也称为方程组(4-5)解空间. 下面我们来求解空间的一个最大线性无关组。 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A 的前r个列向量线性无关，于是A的行最简形为 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I + +               =            

与对应的线性方程组为 +.+b=0 X,tbnXr41++b,nxn=0 移项后可得 =-B.r-bnXm (4-7) x,=-b4H火41-bnx

1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x + + + +  = − −−     −  = − −−  与I对应的线性方程组为 1 1, 1 1 1, , 1 1 , 0 0 r r n n r r r r r n n x b x b x x b x b x + + + +  + + + =      + + + =  移项后可得

在方程组(4-)中，给定x+1,水n一组确定的数， 可惟一确定x1心，的值，便得到方程组(4-7)的一个 解，也就是方程组(4-5)的一个解，我们把x+1xm 称为自由未知量 令x+1,心n分别取下列-r组数

令xr+1,.,xn分别取下列n-r组数 1 2 1 0 0 0 1 0 0 0 1 r r n x x x + +                   =                                   ， ， ， 在方程组(4-7)中，给定xr+1,.,xn一组确定的数， 可惟一确定x1 ,.,xr的值，便得到方程组(4-7)的一个 解，也就是方程组(4-5)的一个解，我们把xr+1,.,xn 称为自由未知量

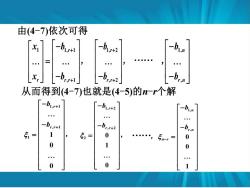
由(4-7)依次可得 x, -b 从而得到(4-7)也就是(4-5)的-个解 -b1,+1 bi.n 一br+1 -b*2 一brn 51= 1 52= 0 5-,= 0 0 1 0 0 0 1

1 1, 1 , 1 r r r r x b x b + +     −        =        −     ， 1, 2 , 2 r r r b b + +   −        −  ， 1, , n r n b b   −        −  ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b  + +   −        −   =              ， 1, 2 , 2 2 0 1 0 r r r b b  + +   −        −   =              ， 1, , 0 0 1 n r n n r b b  −   −        −   =             

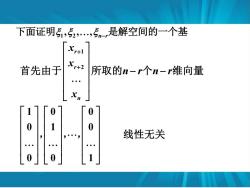
下面证明5,52，5m,是解空间的一个基 + 首先由于 Xr+2 所取的n-r个n-r维向量 七n 0 0 0 1 0 线性无关

1 2 , , , n r    下面证明  − 是解空间的一个基 1 2 1 0 0 0 1 0 0 0 1 r r n x x n r n r x + +       − −                                               首先由于 所取的 个 维向量 ， ， ， 线性无关