《复变函数与积分变换》课程教学课件（PPT讲稿）第八章 拉普拉斯变换 8.4 拉普拉斯变换的应用

第四节拉普拉斯变换的应用 许多工程实际问题常用微分方程来描述，而拉普 拉斯变换对于求解微分方程是非常有效的， 其方法是：先通过拉普拉斯变换将微分方程化为 像函数的代数方程，由代数方程求出像函数，再取 拉普拉斯逆变换就可以求出微分方程的解

第四节拉普拉斯变换的应用 . , 拉斯变换对于求解微分方程是非常有效的 许多工程实际问题常用微分方程来描述 而拉普 . , , : 拉普拉斯逆变换就可以求出微分方程的解 像函数的代数方程由代数方程求出像函数 再取 其方法是 先通过拉普拉斯变换将微分方程化为

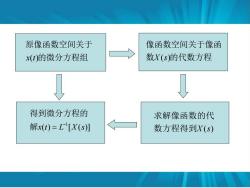
原像函数空间关于 像函数空间关于像函 x(t)的微分方程组 数X(s的代数方程 得到微分方程的 求解像函数的代 解x(t)=L[X(s)】 数方程得到X(s)

数方程得到X (s) 求解像函数的代 ( ) [ ( )] 1 x t L X s − 解 = 得到微分方程的 的微分方程组 原像函数空间关于 x(t) 数 的代数方程 像函数空间关于像函 X (s)

例题1.求解初值问题df(t) +f(t)=sin ot, dt 其中f(0)=0,在区间0，o)上的解。 解：令LLf(t】=F(s),两边取拉普拉斯变换得 F(6+Fo)-=g4o 解代数方程可得F(s)= (s+1)(s2+02) 再由拉普拉斯逆变换（卷积定理）可得到 ()= 1 02+1 (we +sin wt-coswt)

例题1.求解初值问题 ( ) sin , ( ) f t t dt df t + =  其中f (0) = 0,在区间[0,)上的解。 解:令L[ f (t)] = F(s),两边取拉普拉斯变换得 2 2 ( ) ( )   + + = s sF s F s 解代数方程可得 ( 1)( ) ( ) 2 2   + + = s s F s 再由拉普拉斯逆变换(卷积定理)可得到 ( sin cos ) 1 1 ( ) 2 f t e t t t     + − + = −

例题2.求微分方程y+y=t的解，并满足初始条 件y(0)=1,y(0)=-2的解 解：令L[y(t)】=Y(s),两边取拉普拉斯变换得，并考 虑初始条件得到y]+[y]=L[t] 0-0=y0-o= s'Y(s)-s+2+Y(5)= 整理后解得Y(s 1 S-2 1 3 Y()=g2(5+0 S s2+1 s2+1s2+1

(0) 1, (0) 2 . ' '' 件 的解 例题2.求微分方程 的解,并满足初始条 = = − + = y y y y t 虑初始条件得到 解:令L[ y(t)] = Y(s),两边取拉普拉斯变换得,并考 [ ] [ ] [ ] '' L y + L y = L t 2 2 ' 1 ( ) (0) (0) ( ) s s Y s − sy − y +Y s = 2 2 1 ( ) 2 ( ) s s Y s − s + +Y s = 整理后解得Y(s) 1 2 ( 1) 1 ( ) 2 2 2 + − + + = s s s s Y s 1 3 1 1 2 2 2 + − + = + s s s s

再由拉普拉斯逆变换可得到yt) 0=-,F =t+cost-3sin t 例题3.求解常系数微分方程的初值问题 x(t)-2x(t)+2x(t)=2 cost,x(0)=x(0)=0 解：令X(s)=[x()小，在方程两边取拉氏变换，并由初始条 件得到

例题3.求解常系数微分方程的初值问题 ( ) 2 ( ) 2 ( ) 2 cos , (0) (0) 0 '' ' ' x t − x t + x t = e t x = x = t 件得到 解:令X (s) = L[x(t)],在方程两边取拉氏变换,并由初始条 再由拉普拉斯逆变换可得到y(t) ] 1 3 ] [ 1 ] [ 1 ( ) [ ( )] [ 2 1 2 1 2 1 1 + − + = = + − − − − s L s s L s y t L Y s L = t +cost −3sin t

s2X(s)-2sX(s)+2X(s)= 2(s-1) (s-1)2+1 求解此方程得到Xs) 2(s-1) [(s-1)2+1]2 -0 0=L[X(s]=L'[ 2(s-1) -l-er eein

] [( 1) 1] 2( 1) ( ) [ ( )] [ 2 2 1 1 − + − = = − − s s x t L X s L ) ] 1 1 ] [( ( 1) 2 [ ' 2 1 2 2 1 + − = + = − − s e L s s e L t t t e t s t e L t t ] sin 1 1 [ 2 1 = + = − 2 2 [( 1) 1] 2( 1) ( ) − + − = s s 求解此方程得到 X s ( 1) 1 2( 1) ( ) 2 ( ) 2 ( ) 2 2 − + − − + = s s s X s sX s X s

例3：求解微分方程组 [x(t)+x(t)-y(t)=e' x(0)=y0)=1 y(t)+3x(t)-2y(t)=2e1 解：令X(s)=L[x(t),Y(s)=Ly(t)]在方程两边取拉 氏变换，并由初始条件得到 x()-1+)-Ys)=1 -1 sY)-1+3X(s)-2Y06)=21 -1

   + − = + − = t t y t x t y t e x t x t y t e ( ) 3 ( ) 2 ( ) 2 ( ) ( ) ( ) ' ' x(0) = y(0) =1 氏变换,并由初始条件得到 解:令X (s) = L[x(t)],Y(s) = L[ y(t)]在方程两边取拉 例3:求解微分方程组 1 1 ( ) 1 ( ) ( ) − − + − = s sX s X s Y s 1 1 ( ) 1 3 ( ) 2 ( ) 2 − − + − = s sY s X s Y s

尖解得到)=) 再取拉普拉斯逆变换得到原来方程组的解 x(t)=y(t)-e 例4：求解微分方程组 x'(t)+y(t)+x(t)+y()=0 2x"(t)-y'(t)-x(t)+x(t)=sint 满足初始条件x(O)=y(O)=0,x(0)=y(0)=-1的解

求解得到 1 1 ( ) ( ) − = = s X s Y s 再取拉普拉斯逆变换得到原来方程组的解 t x(t) = y(t) = e    − − + = + + + = x t y t x t y t t x t y t x t y t 2 ( ) ( ) ( ) ( ) sin ( ) ( ) ( ) ( ) 0 '' '' '' '' 例4 :求解微分方程组 (0) (0) 0, (0) (0) 1 . 满足初始条件x = y = x ' = y ' = − 的解

解：令X(s)=[x(t)1,Y(s)=[y(t)在方程两边取拉 氏变换，并由初始条件得到 s2X(s)+1+s2Y(s)+1+X(s)+Y(s)=0 2s2Xs+2-s2Ys)-1-X()+Ys)=g+ 求解此方程组得到 ()=-1 取拉普拉斯逆变换得到原方程组的解为 x(t)=y(t)=-sin t

氏变换,并由初始条件得到 解:令X (s) = L[x(t)],Y(s) = L[ y(t)]在方程两边取拉 ( ) 1 ( ) 1 ( ) ( ) 0 2 2 s X s + + s Y s + + X s +Y s = 1 1 2 ( ) 2 ( ) 1 ( ) ( ) 2 2 2 + + − − − + = s s X s s Y s X s Y s 求解此方程组得到 1 1 , ( ) 1 1 ( ) 2 2 + = − + = − s Y s s X s 取拉普拉斯逆变换得到原方程组的解为 x(t) = y(t) = −sin t

例5：求解微分方程组 y(t)+x(t)+x(t)-y(t)=e'-2 2y(t)-x"(t)-2y(t)+x(t)=-t 满足初始条件x(0)=y(0)=0,x(0)=y(O)=0的解 解：令X(s)=L[x(t)小，Y(s)=L[y(t)]在方程两边取拉 氏变换，并由初始条件得到 5Y)-sX)+r)-Y6=1,2 s-1 22Y)-sXs)-2xrs)+X6)=- 2

例5:求解微分方程组    − − + = − + + − = − y t x t y t x t t y t x t x t y t e t 2 ( ) ( ) 2 ( ) ( ) ( ) ( ) ( ) ( ) 2 '' '' ' '' '' ' (0) (0) 0, (0) (0) 0 . 满足初始条件x = y = x ' = y ' = 的解 氏变换,并由初始条件得到 解:令X (s) = L[x(t)],Y(s) = L[ y(t)]在方程两边取拉 s s s Y s s X s sX s Y s 2 1 1 ( ) ( ) ( ) ( ) 2 2 − − − + − = 2 2 2 1 2 ( ) ( ) 2 ( ) ( ) s s Y s − s X s − sY s + X s = −