《高等数学》课程教学资源（PPT课件）第九章_D9_2偏导数

第九章 第二节 偏导赵 偏导数概念及其计算 二、高阶偏导数 HIGH EDUCATION PRESS eC8 机动目录上页下页返回结束

第二节 机动 目录 上页 下页 返回 结束 一、 偏导数概念及其计算 二 、高阶偏导数 偏 导 数 第九章

偏导数定义及其计算法 定义1.设函数z=f(x,y)在点(x0,o)日 的某邻域内 极限 lim f(xo+△x,yo)-f(x,yo) △x->0 △x 存在，则称此极限为函数z=f(x,y)在点(xo,o)对x 的偏导数，记为 0z of 0x(o,y0) )) fx(x0,y0);f(x0,0) 注意：f(o,yo)=lim f(x0+△x,o)-f(xo,Jyo） △x→0 △x HIGH EDUCATION PRESS 机动目录上页下页返回结束

定义1. z = f (x, y) 在点 存在, z f (x, y) 在点(x , y ) 对x = 0 0 的偏导数，记为 ( , ) 0 0 x y 的某邻域内 ; ( , ) 0 0 x x y f   x + x 0 0 x 则称此极限为函数 极限 设函数 f (x0 ) = ( ) ( ) 0 0 f x + x − f x 0 x lim x→ x ; ( , ) 0 0 x x y z d 0 d x x x y = = ( , ). 1 0 0 f  x y 机动 目录 上页 下页 返回 结束 x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y 注意 x : 一、 偏导数定义及其计算法

fx(xo,Yo)=lim f(xo+△x,y0)-f(x0,0) △x→0 △x 同样可定义对y的偏导数 f(o,)=lim f(x0,0+△y)-f(xo,%) △y-→0 △y 偏导函数：若函数z=f(x,y)在域D内每一点(x,y处 对x或y偏导数存在，则该偏导数称为偏导函数 也简称为偏导数， 记为 0z of. Ox'Ox ,f(x,y),f(x,y) 0z 8y' of, 8v y,f(x,y),5(x,y) HIGH EDUCATION PRESS D◆0C08 机动目录上页下页返回结束

同样可定义对 y 的偏导数 lim  →0 = y ( , ) 0 0 f x y y 若函数 z= f (x , y) 在域 D 内每一点 (x ,y)处 则该偏导数称为偏导函数, 也简称为偏导数 , ( , ) , ( , ) 2 f x y f x y y  ( , ) 0 f x ( , ) 0 − f x y 记为 y + y 0 0 y 机动 目录 上页 下页 返回 结束 对 x或 y 偏导数存在, , , , y z y f y z     x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y x 偏导函数:

偏导数的定义 f(XoYo)=lim f(+△x,o)-fxo,o) △x→0 △x 偏导数的符号 02 xx=X0 f(x0,%) (xo yo) y=yo 冬偏导函数 f东(x,y)=lim fx+△x,y)-f(x,y) △x→>0 △x 偏导函数的符号 ax’ax’ x,或f(x), HIGH EDUCATION PRESS

❖偏导数的定义 ❖偏导数的符号 x z    x f    x z  或 f (x, y) x  ❖偏导函数 x f x x y f x y f x y x x  + − =  → ( , ) ( , ) ( , ) lim 0  ❖偏导函数的符号 ( , ). 1 0 0 f  x y 0 0 y y x x x z = =    0 0 y y x x x f = =    0 0 y y zx x x = =  ( , ) 0 0 f x y x  x f x x y f x y f x y x x  + − =  → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 

偏导数的概念可以推广到二元以上的函数 例如，三元函数=f(x,y,)在点(x,y,)处对x的 偏导数定义为 /(x,2）=1im/x+Ax,⅓)-fxy,a Ax->0 △x f(xy,2)=? (请自己写出) f(x,y,2)=? HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . x x + x f (x, y,z) = ? y f (x, y,z) = ? z x 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出)

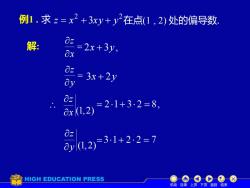
例1.求z=x2+3xy+y2在点(1,2)处的偏导数 解 a22+3y 02 0y =3x+2y 612》=21+328 231-22=7 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1 . 求 2 2 z = x + 3xy + y 解: =   x z x (1,2) z    在点(1 , 2) 处的偏导数. 2x + 3y , =   y z 3x + 2y y (1,2) z   机动 目录 上页 下页 返回 结束

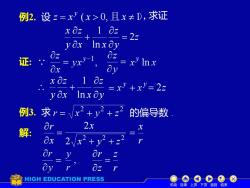
例2.设z=x'(x>0,且x≠D,求证 x0z,1 0z =22 yox Inxay 0z 0z 证： Ox =x-1 8y x0z 1 0z yOx Inxoy =xy+x'=22 例3. 求r=x2+y2+z2 的偏导数 Or 2x 解： 8x 2Vx2+y2+2 Or 1 Or 0y 0z HIGH EDUCATION PRESS e0C08 机动目录上页下页返回结束

例2. 设 z = x y ( x  0, 且 x 1）， z y z x x z y x 2 ln 1 =   +   证: y z x x z y x   +    ln 1 例3. 求 的偏导数 . 解: =   x r 求证 = 2z 2 2 2 2 x + y + z 2x r x = r z z r =   机动 目录 上页 下页 返回 结束

例4.已知理想气体的状态方程pV=RT(R为常数)， 求证 op av aT =-1 av RT 证： RT V v2 说明：此例表明， V= RT R 偏导数记号是一个 p 整体记号，不能看作 T- V 分子与分母的商！ R op R Op av RT =-1 op HIGH EDUCATION PRESS 机动目录上页下页返回结束

偏导数记号是一个 例4. 已知理想气体的状态方程 求证: = −1         p T T V V p 证: , V RT p = , p RT V = =          p T T V V p 说明: (R 为常数) , =   V p 2 V RT − =   T V p R pV RT − = −1 不能看作 分子与分母的商 ! 此例表明, 机动 目录 上页 下页 返回 结束 整体记号

二元函数偏导数的几何意义： x-x0 y=Yo fx,0x=x0 d 是曲线 z=(x,y在点M处的切线 y=Yo MoT,对x轴的斜率 of x=X0 0y ) y=Yo y=Yo 是曲线 z=f(x,y) 在点M处的切线M,T,对y轴的 x=X0 斜率 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二元函数偏导数的几何意义: 0 0 ( , ) d d 0 0 x x f x y x x f x x y y = =   = =    = = 0 ( , ) y y z f x y M0Tx 0 0 ( , ) d d 0 0 y y f x y y y f x x y y = =   = = 是曲线 M0Ty 在点 M0 处的切线 对 x 轴的斜率. 在点M0 处的切线 斜率. 是曲线 y x z 0 x Ty o Tx 0 y M0 机动 目录 上页 下页 返回 结束 对 y 轴的

?偏导数的求法 求函数对一个自变量的偏导数时，只要把其它自变 量看作常数，然后按一元函数求导法求导即可 求一点处偏导数的方法： f.(x.Xo)=/(x.y(xo.o)=[df(x.yo)mx =Vo f=,f6w)=f0以 注意：函数在某点各偏导数都存在，但在该点不一定连续 即偏导数存在 在续 HIGH EDUCATION PRESS

❖偏导数的求法 求函数对一个自变量的偏导数时 只要把其它自变 量看作常数 然后按一元函数求导法求导即可 求一点处偏导数的方法： 0 0 ( , ) ( , ) 0 0 y y x x x x f x y f x y = = =  0 ( , ) [ ( , )] 0 0 0 x x x f x y dx d f x y = =  0 ) 0 ( , ) ( , 0 0 y y x x y y f x y f x y = = =  0 ( , ) [ ( , )] y 0 0 0 y y f x y dy d f x y = =  注意：函数在某点各偏导数都存在, 但在该点不一定连续. 即 偏导数存在 连续