《高等数学》课程教学资源（PPT课件）第十二章_D12_4函数展开成幂级数

第四节 第十二章 离数展开成暴级数 两类问题：在收敛域内 00 幂级数∑anx” 求和 和函数S(x) n=0 展开 本节内容： 一、泰勒(Taylor)级数 二、 函数展开成幂级数 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第四节 两类问题: 在收敛域内 和函数 求 和 展 开 本节内容: 一、泰勒 ( Taylor ) 级数 二、函数展开成幂级数 函数展开成幂级数 机动 目录 上页 下页 返回 结束 第十二章

泰勒(Taylor)级数 公复习 若函数f(x)在xo的某邻域内具有n+1阶导数 则在该邻域内有： f)=f)+foXx-x)+d(x-月 21 ,+f(o(x-x)”+Rn() n! 此式称为f(x)的n阶泰勒公式： 其中 风0-)”（在与2回 称为拉格朗日余项 HIGH EDUCATION PRESS 下页返回结束

一、泰勒 ( Taylor ) 级数 f (x) = f (x0 ) + f (x0 )(x − x0 ) + 2 0 0 ( ) 2! ( ) x x f x −  n n x x n f x ( ) ! ( ) 0 0 ( ) ++ − R (x) + n 其中 Rn (x) = (  在 x 与 x0 之间) 称为拉格朗日余项 . 1 0 ( 1) ( ) ( 1)! ( ) + + − + n n x x n f  若函数 的某邻域内具有 n + 1 阶导数, 此式称为 f (x) 的 n 阶泰勒公式 , 则在该邻域内有 : 机动 目录 上页 下页 返回 结束 ❖复习

泰勒级数 若函数f(x)在x的某邻域内具有任意阶导数，则幂级数 f)+Xx-x+"w(x-月+x-+ 称为f(x)的泰勒级数 冬麦克劳林级数 在泰勒级数中取x。=0,得 f0+f0r+0r2++ fm)(0) 20 xn+ 此级数称为f(x)的麦克劳林级数 待解决的问题：1)对此级数，它的收敛域是什么？ 2)在收敛域上，和函数是否为f(x)? HIGH EDUCATION PRESS 机动目录上页下页返回结束

f (x0 ) +f (x0 )(x − x0 ) + 2 0 0 ( ) 2! ( ) x x f x −  ++ − n + n x x n f x ( ) ! ( ) 0 0 ( ) 称为f (x) 的泰勒级数 . 则幂级数 1) 对此级数, 它的收敛域是什么 ？ 2) 在收敛域上 , 和函数是否为 f (x) ? 待解决的问题 : 若函数 的某邻域内具有任意阶导数, 机动 目录 上页 下页 返回 结束 +  + +   +  + ! (0) 2! (0) (0) (0) ( ) 2 n n x n f x f f f x  . 在泰勒级数中取x0=0 得 此级数称为 f (x) 的麦克劳林级数. ❖泰勒级数 ❖麦克劳林级数

定理1.设函数f(x)在点x的某一邻域U(x)内具有 各阶导数，则f(x)在该邻域内能展开成泰勒级数的充要 条件是f(x)的泰勒公式中的余项满足：IimR,(x)=0 n->o0 f(x)=f(xo)+f(xo)(x-x0)+ f"(o(x-x0) 21 f(x-x+. 推广：在上述泰勒级数中取x。0,得 f(x)在(-；r)内能展成麦克劳林级数，即展开成x的幂级数 f(x)=f0)+f(0)x+f(0)x2++品(0)x”+ HIGH EDUCATION PRESS 机动目录 上而下而间结南

定理1 . 各阶导数, 则 f (x) 在该邻域内能展开成泰勒级数的充要 条件是 f (x) 的泰勒公式中的余项满足: lim ( ) = 0. → R x n n 设函数 f (x) 在点 x0 的某一邻域 内具有 机动 目录 上页 下页 返回 结束 f (x0 ) + f (x0 )(x − x0 ) + 2 0 0 ( ) 2! ( ) x x f x −  ++ − n + n x x n f x ( ) ! ( ) 0 0 ( ) f (x) = 推广： f (x)在(-r, r)内能展成麦克劳林级数, 即展开成 x的幂级数 在上述泰勒级数中取 x0= 0 得

二、函数展开成幂级数 ?函数展开成幂级数的步骤 第一步求出f(x)的各阶导数：f'(x),f'"(x),··,fx), 第二步求函数及其各阶导数在x=0处的值： 0),f'(0),f"(0),·.·,fn(0),·· 第三步写出幂级数并求出收敛半径R, f0)+f0x+f" 2x2+.+ fm(0) xn+. 21 h 第四步考察在区间(-R,R)内时是否R,(x)→0(n→∞)， 如果Rnx)→0(n→o),则x)在(-R,R)内的幂级数展开式 为 f)=f0+f0x+'"Ox2++f 2xn+.(-R<x<R) 21 HIGH EDUCATION PRESS

❖函数展开成幂级数的步骤 •第一步 求出f (x)的各阶导数: f (x) f (x)     f (n) (x)    ; •第二步 求函数及其各阶导数在x=0 处的值: f(0) f (0) f (0)     f (n) ( 0)    ; •第三步 写出幂级数 •第四步 考察在区间(−R R)内时是否Rn (x)→0(n→). 如果Rn (x)→0(n→) 则 f(x) 在(−R R)内的幂级数展开式 为 ! (0) 2! (0) ( ) (0) (0) ( ) 2 +  + +   = +  + n n x n f x f f x f f x (−RxR). ! (0) 2! (0) (0) (0) ( ) 2 +  + +   +  + n n x n f x f f f x  并求出收敛半径R; 二、函数展开成幂级数

例1.将函数f(x)=ex展开成x的幂级数 解：fm(x)=e,fm(0)=1(n=0,1,故得级数 1+x 其收敛半径为 R=lim =+00 n→0 nl (n+1） 对任何有限数x,其余项满足 n+l oo (n+1) (5在0与x之间) 2 故ex=1+x+x +·，,X∈(-00，十00） 21 31 n HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 将函数 展开成 x 的幂级数. 解: ( ) , (n) x  f x = e (0) 1 ( 0,1, ), f (n) = n =  1 其收敛半径为 对任何有限数 x , 其余项满足  e (n +1)! n+1 x x  e 故 , ! 1 3! 1 2! 1 1 x = + + 2 + 3 ++ x n + n e x x x → = n R lim ! 1 n ( 1)! 1 n + n → ( 在0与x 之间) + x 2 2! 1 + x 3 3! 1 + x ++ x n + n! 1 故得级数 机动 目录 上页 下页 返回 结束

例2.将f(x)=sinx展开成x的幂级数 解： .f()(x)=sin(x+n.) 所以fn(0)顺序循环地取0,1,0，-1，.(n=0,1,2,3,) 得级数x-引x2x3-+(-1 2n+1 十·· (2n+1)l 其收敛半径为R=+∞， 对任何有限数x,其余项满足 1n+1 R () sin(+(n+1)) x n-→ (n+1)川 (n+1) snx=x-x23+x3-+(-2万x2n 1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 将 展开成 x 的幂级数. 解: ( ) = ( ) f x n  得级数: x 其收敛半径为 R = +, 对任何有限数 x , 其余项满足 sin( ( 1) ) 2   + n + (n +1)! n+1 x 3 3! 1 − x + −+ 5 5! 1 x  sin x n → = x − 3 1 ! x 3 + 5 1 ! x 5 −+ (−1) n−1 (2n 1 −1)! x 2n−1 + 机动 目录 上页 下页 返回 结束 所以f (n) (0)顺序循环地取0, 1, 0, −1,    (n=0, 1, 2, 3,   ) + + + − + (2 1)! ( 1) 2 1 n x n n

例3.将函数f(x)=Q+x)”展开成x的幂级数，其中m 为任意常数 解：x)的各阶导数为 f'(x)=m(1+x)yml,f"(x=mm-1)1+xym-2,··, fmx=m(m-1)(m-2)·(m-n+1)(1+x)ym-,. 则 f(0)=1,f'(0)=m,f"(0)=m(m-1), fnm)(0)=m(m-1)(m-2).(m-n+1),. 于是得级数 1+x+ m(m-D2m(m-1.(m-n1) 2」 n! 可以证明 1+x)m=1+mx+ mm-x2+.+mm-.(m-n+1x”+ 2! n (-1<x<1) HIGH EDUCATION PRESS

例3. 将函数 展开成 x 的幂级数, 其中m 为任意常数 . 则 f (0) =1, f (0) = m, f (0) = m(m −1) , f (n) (0) = m(m −1)(m − 2)(m − n +1) ,  于是得级数 1+ mx + + − 2 2! ( 1) x m m   + − − + + n x n m m m n ! ( 1) ( 1) 解: f(x)的各阶导数为 f (x)=m(1+x) m−1  f (x)=m(m−1)(1+x) m−2      f (n) (x)=m(m−1)(m−2)  (m−n+1)(1+x) m−n    可以证明 + − 2 2! ( 1) x m m   + − − + + n x n m m m n ! ( 1) ( 1) + x = + m x + m (1 ) 1

(1+x)m=1+mx+ mm-Dx2+.+mm-少-.(m-n+ x” 2 n! (-1<x<1) 称为二项展开式 说明： (1)在x=±处的收敛性与m有关 (2)当m为正整数时，级数为x的m次多项式，上式 就是代数学中的二项式定理 HIGH EDUCATION PRESS DeOC8 机动目录上页下页返回结束

+ − 2 2! ( 1) x m m   + − − + + n x n m m m n ! ( 1) ( 1) + x = + m x + m (1 ) 1 称为二项展开式 . 说明： (1) 在 x＝±1 处的收敛性与 m 有关 . (2) 当 m 为正整数时, 级数为 x 的 m 次多项式, 上式 就是代数学中的二项式定理. 机动 目录 上页 下页 返回 结束

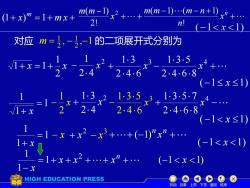
(1+x)m=1+mx+ mm-1x2++mm-1小-.(m-n+x+ 21 n! (-1≤x≤1) 对应m=,-2,-1的二项展开式分别为 1.3 x3- 13.5 246 2.4.6.8 (-1≤x≤1) 4 X 2.46.8 (-1<x≤1) 1=1-x+x2-x3++(-1x”+. 1+ (-1<x<1)〉 1+x+x2+.+xn+ (-1<x<1) 為HIGH EDUCATION PRESS 机动目录上页下页返回结束

对应 , , 1 2 1 2 1 m = − − 的二项展开式分别为 x x 2 1 1+ =1+ 2 2 4 1 x  − 3 2 4 6 1 3 x    + (−1 x 1) +      − 4 2 4 6 8 1 3 5 x 1 1 1 = + x 2 2 4 1 3 x   + 3 2 4 6 1 3 5 x     − (−1 x 1) −       + 4 2 4 6 8 1 3 5 7 x x 2 1 − 1 1 1 = + x 2 + x 3 − x (−1 x 1) − x ++ (−1) n x n + 机动 目录 上页 下页 返回 结束 1 ( 1 1) 1 1 2 = + + + + + −   − x x x x x  n  + − 2 2! ( 1) x m m   + − − + + n x n m m m n ! ( 1) ( 1) + x = + m x + m (1 ) 1