《高等数学》课程教学资源（PPT课件）第八章 空间解析几何与向量代数_2.理解单位向量、方向数与方向余弦、向量的坐标表示式，掌握用坐标表示式进行向量线性运算的方法。_》8-1向量及其线性代数

第、章 空间解析儿何与向量代数 第一部分向量代数 第二部分空间解析几何 在三维空间中： 空间形式一 点线，面 T 数量关系一 坐标，方程（组） 基本方法一 坐标法：向量法

数量关系 — 第八章 第一部分 向量代数 第二部分 空间解析几何 在三维空间中: 空间形式 — 点, 线, 面 基本方法 — 坐标法; 向量法 坐标, 方程（组） 空间解析几何与向量代数

第一节 第七章 向量及其线性运算 一、 向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 HIGH EDUCATION PRESS 机动目录上页下页返回结束

四、利用坐标作向量的线性运算 第一节 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 机动 目录 上页 下页 返回 结束 向量及其线性运算 第七章

一、向量的概念 向量：既有大小，又有方向的量称为向量（又称矢量） 表示法有向线段M1,或a,或a. 向量的模：向量的大小，记作MM2,或a,或a 向径（矢径）：起点为原点的向量 自由向量：与起点无关的向量 单位向量：模为1的向量，记作a°或a° 零向量：模为0的向量，记作0，或0. HIGH EDUCATION PRESS 机动目 页下页返回结束

表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M2 既有大小, 又有方向的量称为向量 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a , 机动 目录 上页 下页 返回 结束

若向量ā与b大小相等，方向相同，则称ā与b相等 记作a=b; 若向量ā与五方向相同或相反，则称ā与平行，记作 ā/b；规定：零向量与任何向量平行； 与ā的模相同，但方向相反的向量称为ā的负向量， 记作-a; 因平行向量可平移到同一直线上，故两向量平行又称 两向量共线 若k仑3)个向量经平移可移到同一平面上，则称此k 个向量共面 等HIGH EDUCATION PRESS 机动目 下页返回结束

规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作－a ; 机动 目录 上页 下页 返回 结束

二、向量的线性运算 1.向量的加法 平行四边形法则： (a+b)+ a+币 a+(b+) a+b 三角形法则 a+b a 运算规律：交换律 a+b-b+a 结合律(a+b+c=a+(亿+=a+b+& 三角形法侧可推广到多个向量相加 HIGH EDUCATION PRESS 机动目 下页返回结束

二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . 机动 目录 上页 下页 返回 结束 b b a + b = b + a (a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) (a + b) + c a a a + b a + b

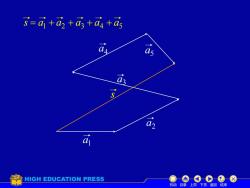
S=a +a +as+as+as 05 HIGH EDUCATION PRESS 机动目录上页下页返回结束

机动 目录 上页 下页 返回 结束 s a3 a4 a5 a2 a1 1 2 3 4 5 s = a + a + a + a + a

2.向量的减法 b-a-b+(-a) 6- b-a 特别当b=a时，有 a-a=a+(-=0 三角不等式 a+bs a+b a-b s a+b HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 向量的减法 三角不等式 机动 目录 上页 下页 返回 结束 a

3.向量与数的乘法 )是一个数，？与a的乘积是一个新向量，记作人ā. 规定：2>0时，2a与a同向，2a=2a; 2<0时，2a与a反向，2a=-a: 2=0时，2a=0. 总之 |2a=2a 运算律：结合律(ua)=4(2a)=2ud 分配律(2+)a=2ā+ud 2(a+b)=元a+元b 若a#0,则有单位向量a=可a. 因此a=aa HIGH EDUCATION PRESS 机动目录上页下页返回结束

a a    =  3. 向量与数的乘法  是一个数 , a .   规定 : 1a a ;   = 可见 1a a ;   − = −  与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a)    ( a)  =   a  =   分配律 (a b)    + a b   =  +  =  则有单位向量 a . 1 a a   因此    a = a a 机动 目录 上页 下页 返回 结束

定理1.设a为非零向量，则 a/b二b=2a ()为唯一实数) 证“一设a/6,取=士/a,a,万同向时 取正号，反向时取负号，则与入a同向，且 -是a 故b=na. 再证数入的唯一性.设又有=4a,则(2-0)a=0 而a≠0，故2-4=0，即2=4 HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证: “ ”. , 取 ＝± 且 再证数  的唯一性 . 则 故  −  = 0, 即 =  . a∥b 设 a∥b 取正号, 反向时取负号, , a , b 同向时 则 b 与  a 同向, 设又有 b＝ a , ( − ) a = 0 = = b 故 b =  a. 机动 目录 上页 下页 返回 结束

“一”已知b=入a,则 当2=0时，b=0 当2>0时，a,b同向 当2<0时，a,b反向 例1.设M为□ABCD对角线的交点，AB=a,AD=b, 试用a与b表示M,MB,MC,M 解：a+b=AC=2MC=-2M☑ b-a=BD=2MD=-2MB MA=-(a+b)Mc=-(石-a) MC=j(a+B) MD=(B-a) HIGH EDUCATION PRESS 机动目录上页下页返回结束

“ ” 则 例1. 设 M 为 M A B 解: D C ABCD 对角线的交点, b a AC = −2 MA BD = −2MB 已知 b＝ a , b＝0 a , b 同向 a , b 反向 a∥b 试用a 与b 表示 MA,MB,MC,MD. a + b = b − a = ( ) 2 1  MA = − a + b ( ) 2 1 MB = − b − a ( ) 2 1 MC = a + b ( ) 2 1 MD = b − a 机动 目录 上页 下页 返回 结束