《线性代数》课程PPT教学课件（B）第一章 行列式_1-1行列式的定义

第一章行列式 本章主要从以下四个方面进行讨论 一、行列式的定义 二、行列式的性质 三、行列式的计算 四、行列式的应用

本章主要从以下四个方面进行讨论 二、行列式的性质 第一章行列式 一、行列式的定义 三、行列式的计算 四、行列式的应用

第一节行列式的定义 一、行列式的引入 用消元法解二元线性方程组 411X1+412X2=b1,(1) (1-1) 4211+22x2=b2·(2) (1)×a2:41421+124222=b022, (2)×a12:41242x1+24222=b22, 两式相减消去七2，得

一、行列式的引入 用消元法解二元线性方程组 11 1 12 2 1 21 1 22 2 2 , (1) (1-1) . (2) a x a x b a x a x b        1 : 22  a , 11 22 1 12 22 2 1 22 a a x  a a x  b a 2 : 12  a , 12 21 1 12 22 2 2 12 a a x  a a x  b a 两式相减消去 x2，得 第一节行列式的定义

（411422-412421）X1=b1422-412b2; 类似地，消去x,得 （01122-41221）X2=41b2-b14219 当4142-41221≠0时，方程组的解为 七=4a:-，5=4- 122-L1221 L11L22-L12L24 由方程组的四个系数确定

; 11 22 12 21 1 1 22 12 2 （a a  a a ）x  b a  a b 类似地，消去 x1，得 , 11 22 12 21 2 11 2 1 21 （a a  a a ）x  a b  b a 当 a11a22  a12a21  0时， 方程组的解为 ， 11 22 12 21 1 22 12 2 1 a a a a b a a b x    11 2 1 21 2 11 22 12 21 . a b b a x a a a a    由方程组的四个系数确定

定义引入记号： 2 L21 22 称之为二阶行列式，它表式数值1142-4142 即 D 2 =41122-012L21· L21 l22 行列式中横排的叫作行，纵排的叫作列，(i,j=1,2) 称为行列式的元素，为行标，为列标

11 12 21 22 11 22 12 21 a a a a a a  a a 引入记号： 称之为二阶行列式，它表式数值 ， 即 . 11 22 12 21 21 22 11 12 a a a a a a a a D    行列式中横排的叫作行，纵排的叫作列， ( , 1,2) ij a i j  称为行列式的元素，i为行标，j为列标

二阶行列式的计算一对角线法则 主对角线 L12 =011022-41221 次对角线 L22 对于二元线性方程组 1X1+12X2=b1, 421x1+422X2=b2. 若记 11 42 21 L22 系数行列式

a21 11 a 12 a 22 a 主对角线 次对角线 11 22  a a . 12 21  a a 二阶行列式的计算 若记 , 21 22 11 12 a a a a D         . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 对于二元线性方程组 系数行列式

dnr +duX-b 21x1+a22x2b2 D. 2 az 421X1+M22X2 D2= 11 b

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b , 2 22 1 12 1 b a b a D         . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b . 21 2 11 1 2 a b a b D 

则二元线性方程组的解为 b 2 b Dy b2 22 X1= D2 421 D 1 2 X2= D 1 12 421 L22 L21 L22 注意 分母都为原方程组的系数行列式

则二元线性方程组的解为 , 21 22 11 12 2 22 1 12 1 1 a a a a b a b a D D x   注意 分母都为原方程组的系数行列式. . 21 22 11 12 21 2 11 1 2 2 a a a a a b a b D D x  

例1求解二元线性方程组 3x1-2x2=12, 2x1+2=1. 解 =3-(-4)=7≠0， Di= .X1= D-1 _D-21=-3 D 7 4=2,2=D

       2 1. 3 2 12, 1 2 1 2 x x x x 求解二元线性方程组 解 2 1 3  2 D   3  (4)  7  0, 1 1 12 2 1  D   14, 2 1 3 12 D2   21, D D x 1  1  2, 7 14   D D x 2 2  3. 7 21    

类似地，由三元线性方程组 4111+412x2+13X3=b1, 21七1+022X2+a23X3=b2, (1-2) 31X1+32X2+433X3=b3; (1)引入记号 1 2 3 L21 2 d23 L31 l32 33 称之为三阶行列式：

称之为 . 由三元线性方程组 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3 , , 1 2 ; a x a x a x b a x a x a x b a x a x a x b                （ ） 11 12 13 21 22 23 31 32 33 a a a a a a a a a 类似地

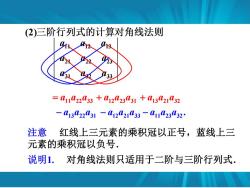
(2)三阶行列式的计算对角线法则 =411022033+412023031+13421L32 -413422431-012021L33-411L23L32 注意 红线上三元素的乘积冠以正号，蓝线上三 元素的乘积冠以负号. 说明1.对角线法则只适用于二阶与三阶行列式

31 32 33 21 22 23 11 12 13 a a a a a a a a a 11 22 33  a a a . 11 23 32  a a a 注意 红线上三元素的乘积冠以正号，蓝线上三 元素的乘积冠以负号． 说明1. 对角线法则只适用于二阶与三阶行列式． 13 21 32  a a a 12 23 31  a a a 13 22 31  a a a 12 21 33  a a a