《高等数学》课程教学资源（作业习题）第九章

第九章多元函戴微分法及并应用班级： 姓名： 序号： 1多元函数的基本概念 一、填空、选择题 L函数：=x-√少的定义域为 之西数=0的定义线为 3.函数1=4-x2-y2-2+ +户：的定义城为 1 4. sin xy= y 5.设函数f(x,y) y y=0 (A)不存在 (B)等于1 (C)等于0 (D)等于2 6.设函数fx,)=+y 10 +0,则f0x0 x2+y2=0 (A)处处连续： (⑧)处处有极限，但不连续： (C)仅在(0,0)点连续： (D)除(0,0)点外处处连续 二、计算下列极限 1- ytan xy 2.(02

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 1 1 多元函数的基本概念 一、填空、选择题 1. 函数 z = x − y 的定义域为 . 2 函数 2 2 arccos x y z u + = 的定义域为 . 3. 函数 1 1 4 2 2 2 2 2 2 + + − = − − − + x y z u x y z 的定义域为 . 4. y xy x y sin lim ( , )→(3,0） = . 5.设函数      = +  = 0 0 0 1 sin 1 sin ( , ) x y x y x y y x f x y ，则极限 lim ( , ) ( , ) (0,0) f x y x y → （ ） (A)不存在 (B)等于 1 (C)等于 0 (D)等于 2 6.设函数      + = +  = + 0 0 0 ( , ) 2 2 2 2 2 2 x y x y x y x y f x y ，则 f x y ( , ) （ ） (A) 处处连续； (B) 处处有极限，但不连续； (C) 仅在（0,0）点连续； (D) 除（0,0）点外处处连续 二、计算下列极限 1. xy xy x y 2 4 lim ( , ) (0,0 − + → ） 2. x y xy x y tan lim ( , )→(0,2）

第九章多元函数撒分法及其应用班级： 姓名： 序号： 2-3习题 一、填空、选择题 1、设：=nx+y2),则全微分d止= 2、设fx,y)=xy2+2+x2,则f(1,02)= 3曲线， 4一在点(2,4,5)处的切线对于x轴的倾角为 y=4 4设：m片则会+房 5、=fx,y)在P(oo)处(x,y)、,(x,y)存在是函数在该点可微分的.（) (A)必要条件： (B)充分条件： (C)充要条件： (D)既非必要亦非充分条件 二、求下列函数的偏导数 1、z=simx)+cos2(x 2、=(1+x 3u= 三设：的，求证会y2

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 2 2-3 习题 一、填空、选择题 1、设 ln( ) 2 z = x + y ，则全微分 dz = . 2、设 2 2 2 f (x, y,z) = xy + yz + zx ，则 f xz (1,0,2) = . 3、曲线      = + = 4 4 2 2 y x y z 在点 (2,4,5) 处的切线对于 x 轴的倾角为 . 4、设 x y z = x sin ，则 =   +   y z y x z x . 5、 z = f (x, y) 在 ( , ) 0 0 0 P x y 处 f (x, y) x 、 f (x, y) y 存在是函数在该点可微分的 （ ） （A）必要条件； （B）充分条件； （C）充要条件； （D）既非必要亦非充分条件. 二、求下列函数的偏导数 1、 sin( ) cos ( ) 2 z = xy + xy 2、 y z = (1+ xy) 3、 z y u = x 三、设 ) 1 1 ( x y z e − + = ，求证 z y z y x z x 2 2 2 =   +  

第九章多元函戴横分法及其应用班级： 姓名： 序号： 日，设汤教：，来器等器 五、求下列函数的全微分 1、=xy4 y 2、2=- 3、u=x

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 3 四、设函数 x y z = arctan ，求 , 2 2 2 2 2 x y z y z x z        ， . 五、求下列函数的全微分 1、 y x z = xy+ 2、 2 2 x y y z + = 3、 yz u = x

第九章多元函数撒分法及其应用班级： 姓名： 序号： 4一5习题 1设：=e,面x=如=，则先 么、设z=acan(,而y=e,则 模：rh,面=3-2，*袋等 4、求下列函数的一阶偏导数（其中∫具有一阶连续偏导数） (1)z=f(x2-y2,e9) (2)u=f(x,xy,xyz) 黄：心+，其中/其精=0数票需 6设：=，其中了具有=阶连续偏导数，求器司 800 g

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 4 4—5 习题 1、设 x y z e −2 = ，而 3 x = sin t, y = t ，则 = dt dz . 2、设 z = arctan( xy) ，而 x y = e ，则 = dx dz . 3、设 z u ln v 2 = ，而 v x y y x u = , = 3 − 2 ，求 , y z x z     . 4、求下列函数的一阶偏导数（其中 f 具有一阶连续偏导数） （1） ( , ) 2 2 xy z = f x − y e （2） u = f (x, xy, xyz) 5、设 z = f (x 2 + y 2） ，其中 f 具有二阶导数，求 , 2 2 2 x y z x z      . 6、设 ( , ) y x z = f x ，其中 f 具有二阶连续偏导数，求 2 2 2 2 2 , , y z x y z x z       

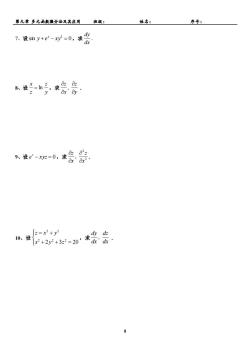
第九章多元函数撒分法及并应用班级： 姓名： 序号： 人设my4e-y=0,求会 8、设-h月*品， 0z 8z r-=0,*器能 2=x2+y2 10、设 +2+3=20求要 dx'dx

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 5 7、设 sin 0 2 y + e − xy = x ，求 dx dy . 8、设 y z z x = ln ，求 , y z x z     . 9、设 e − xyz = 0 z ，求 2 2 , x z x z     . 10、设     + + = = + 2 3 20 2 2 2 2 2 x y z z x y ，求 , dx dz dx dy

第九章多元函数撒分法及其应用班级： 姓名： 序号： 6-7-8习题 一、填空题 1、曲线x=1,y=t子，=t上点」 的切线平行于平面x+2y+2=4, 2、曲面e-:+xy=3在点(2,1,0)处的切平面为 法线为■ 3、函数：=2x2+y2在点L,-1)的梯度为 4、函数：=-x2-2xy+y2在点(2,3)处方向导数的最大值为 5、函数：=2x2-3xy+2y2+4x-3y+1在驻点 处取得极值为 计算题1、求曲线x7少 t ,2=在对应于t=1点处的切线及法平面方程， t x2+y2+z2-3x=0 2、求面线2x-3y十5：-4=0在点1,1D处的切线及法平面方程 3、求椭球面x2+2y2+z2=1上平行于平面x-y+2z=0的切平面方程. 4、()求函数“=+：-g在点L1,2)处沿方向角为a=了B=牙7=号的方向的方向导数 (2)求函数：=x2+y2在点M(1,2)处沿从M。到M,(2,2+5)的方向的方向导数. 6

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 6 6 -–7 - -8 习题 一、填空题 1、曲线 2 3 x = t, y = t ,z = t 上点 的切线平行于平面 x + 2y + z = 4 . 2、曲面 e − z + xy = 3 z 在点 (2 ,1, 0) 处的切平面为 法线为 3、函数 2 2 z = 2x + y 在点 (1, −1) 的梯度为 . 4、函数 2 2 z = x − 2xy+ y 在点 (2, 3) 处方向导数的最大值为 . 5、函数 2 3 2 4 3 1 2 2 z = x − xy+ y + x − y + 在驻点 处取得极 值为 . 二、计算题 1、求曲线 2 , 1 , 1 z t t t y t t x = + = + = 在对应于 t =1 点处的切线及法平面方程. 2、求曲线    − + − = + + − = 2 3 5 4 0 3 0 2 2 2 x y z x y z x 在点 (1,1,1) 处的切线及法平面方程. 3、求椭球面 2 1 2 2 2 x + y + z = 上平行于平面 x − y + 2z = 0 的切平面方程. 4、（1）求函数 u = xy + z − xyz 2 3 在点 (1,1, 2) 处沿方向角为 3 , 4 , 3       = = = 的方向的方向导数. （2）求函数 2 2 z = x + y 在点 (1, 2) M0 处沿从 M0 到 (2, 2 3) M1 + 的方向的方向导数

第九章多元画数撒分法及并应用班级： 姓名： 序号： 5、求函数fx,)=x-2y+2:在附加条件x2+y2+:2=1下的极大值. 6、要造一个体积等于定数k的长方形无盖水池，应如何选择水池的尺寸，方可使它的表面积最小， 7、在x0y平面上求一点，使它到x=0,y=0及x+2y-16=0三直线的距离平方之和为最小。 8、抛物面：=x2+y被平面x+y+z-1截成一椭圆，求这椭圆上的点到原点的距离的最小值与最 大值

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 7 5、求函数 f (x, y,z) = x − 2y + 2z 在附加条件 1 2 2 2 x + y + z = 下的极大值. 6、要造一个体积等于定数 k 的长方形无盖水池，应如何选择水池的尺寸，方可使它的表面积最小. 7、在 xoy 平面上求一点，使它到 x = 0, y = 0 及 x + 2y −16 = 0 三直线的距离平方之和为最小 . 8、 抛物面 2 2 z = x + y 被平面 x + y + z =1 截成一椭圆，求这椭圆上的点到原点的距离的最小值与最 大值