《高等数学》课程教学资源（PPT课件）第十二章_D12_7傅立叶级数

第七节 第十二章 停里叶级怒 一、 三角级数及三角函数系的正交性 二、函数展开成傅里叶级数 三、正弦级数和余弦级数 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第七节 一、三角级数及三角函数系的正交性 机动 目录 上页 下页 返回 结束 二、函数展开成傅里叶级数 三、正弦级数和余弦级数 第十二章 傅里叶级数

三角级数及三角函数系的正交性 简单的周期运动：y=Asin(ot+p)(谐波函数) (A为振幅。o为角频率，o为初相) 复杂的周期运动：y=A0+∑4nsin(0t+pn) n=1 (谐波迭加) An sin pn cosnot+An cos on sinnot o.aningn b c 00 得函数项级数 +∑a,cosx+b,sinm) 2 称上述形式的级数为三角级数 等HIGH EDUCATION PRESS 下页返回结束

一、三角级数及三角函数系的正交性 简单的周期运动 : (谐波函数) ( A为振幅, 复杂的周期运动 : A n t A n t n sinn cos  + n cosn sin  令 sin , an = An n cos , bn = An n 得函数项级数 ( cos sin ) 2 1 0 a nx b nx a n n k +  +  = 为角频率, φ为初相 ) (谐波迭加) 称上述形式的级数为三角级数. 机动 目录 上页 下页 返回 结束

定理1.组成三角级数的函数系 2 (an cosnx+b sin nx k=1 1,cosx,sinx,cos2x,Sin2x,.,cosx,sinx,. 在[-π，]上正交，即其中任意两个不同的函数之积在 [-π，π]上的积分等于0 证：∫1 cosnxdx=1 sinnxdx=0(n=l,2,） π cos kx cosnxdx coskxcosnx=[cos(k+n)x+cos(k-n)x] =J[cos(k+n)x+cos(k-n)x]dx=0(k≠n） 同理可证：，sinkxsinnxdx=0(k≠n) cos kx sin nx dx =0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

cos(k n)x cos(k n)x d x 2 1 = + + − −   定理 1. 组成三角级数的函数系 证:  −   1 cos nxd x =  −   1 sin nxd x = 0 cos kx cos nxdx −   = 0 sin sin d = 0 − kx nx x  同理可证  : 正交 , 上的积分等于 0 . 即其中任意两个不同的函数之积在 cos sin d = 0 − kx nx x   (k  n ) 机动 目录 上页 下页 返回 结束 ( cos sin ) 2 1 0 a nx b nx a n n k +  +  =

但是在三角函数系中两个相同的函数的乘积在[一π，π] 上的积分不等于0.且有 11d=2a cos2nxdx=元 (n=1,2,.） sin2xdk=元 cos2 nx= 1+cos 2nx 1-cos2nx 2 2 HIGH EDUCATION PRESS 机动目录上页下页返回结束

上的积分不等于 0 .    11d = 2 − x sin nxdx 2 −   cos n xdx 2 −   , 2 1 cos 2 cos2 nx nx + = 2 1 cos 2 sin2 nx nx − = 且有 =  =  但是在三角函数系中两个相同的函数的乘积在 机动 目录 上页 下页 返回 结束

二、函数展开成傅里叶级数 定理2.设f(x)是周期为2元的周期函数，且 )cs sin) 00 2 n=1 右端级数可逐项积分，则有 a=fx)cosndx (n=0,1,） b=f()sinndx (n=1,2,.) 由公式②确定的a,b,称为函数f(x) 的傅里叶系数；以f(x)的傅里叶系数为 系数的三角级数①称为f(x)的傅里叶级数 HIGH EDUCATION PRESS 机动目录上页 傅里叶，.B.-

二、函数展开成傅里叶级数 定理 2 . 设 f (x) 是周期为 2 的周期函数 , 且 ( cos sin ) 2 ( ) 1 0 a nx b nx a f x n n n = +  +  = 右端级数可逐项积分, 则有 ① ② 机动 目录 上页 下页 返回 结束 系数的三角级数 ① 称为 的傅里叶系数 ; 由公式 ② 确定的 以 的傅里叶系数为 的傅里叶级数 . 称为函数

定理3（收敛定理，展开定理） 设f(x)是周期为2π的 周期函数，并满足狄利克雷(Dirichlet)条件 1)在一个周期内连续或只有有限个第一类间断点： 2)在一个周期内只有有限个极值点 则f(x)的傅里叶级数收敛，且有 注意：函数展成 傅里叶级数的条 件比展成幂级数 n= 的条件低得多 f(x). x为连续点 x为间断点 2 其中an,bn为f(x)的傅里叶系数，（证明略） HIGH EDUCATION PRESS 上页下页返回结束

定理3 (收敛定理, 展开定理) 设 f (x) 是周期为2的 周期函数, 并满足狄利克雷( Dirichlet )条件: 1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 且有     = f (x) , , 2 ( ) ( ) + − f x + f x x 为间断点 其中 an bn , 为 f (x) 的傅里叶系数 . ( 证明略 ) x 为连续点 注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多. 简介 目录 上页 下页 返回 结束

例1.设fx)是周期为2π的周期函数，它在[-π，π) 上的表达式为 ro-fhi π≤x<0 sx< 将f(x)展成傅里叶级数 解：先求傅里叶系数 comdx -2-+号01-ewxd =0 (n=0,1,2,.） HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 设 f (x) 是周期为 2 的周期函数 , 它在 上的表达式为      − −   =   x x f x 1, 0 1, 0 ( ) 解: 先求傅里叶系数   = − +  −     0 0 1 cos d 1 ( 1)cos d 1 nx x nx x = 0 ( n = 0 ,1, 2 , ) 将 f (x) 展成傅里叶级数. o y x −1 − 1  机动 目录 上页 下页 返回 结束

7 (-)sin mdx+ ]+g-w时 -r1- 当n=1,3,5,. 当n=2,4,6,. (-0<x<+0,x≠0，±π，±2π，.) HIGH EDUCATION PRESS 机动目录上页下页返回结束

  = − +  −     0 0 1 sin d 1 ( 1)sin d 1 nx x nx x 0 1 cos  −     = n nx   0 1 cos   −   + n nx     n n 1 cos 2 = −   n n 1 ( 1) 2 = − −     = , 4 n 0 , 当n =1, 3 , 5 ,  当n = 2 , 4 , 6 ,   f x =  sin x + 4 ( )  sin 3x + 3 1  − + − + k x k sin(2 1) 2 1 1  (−  x  + , x  0 ,  ,  2 , ) 机动 目录 上页 下页 返回 结束

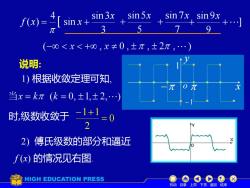
sinx+ in3x, sin5x,sin7x sin9x 3 5 (-0<x<十0，x≠0，土π，士2π，.) 说明： 1)根据收敛定理可知」 当x=kπ(k=0,±1，±2，.） 时级数收敛于 -1+1=0 2 2)傅氏级数的部分和逼近 f(x)的情况见右图 HIGH EDUCATION PRESS e0C8 机动目录上页下页返回结束

7 sin 7x + ] 9 sin 9 + + x 1) 根据收敛定理可知, 时,级数收敛于 0 2 1 1 = − + 2) 傅氏级数的部分和逼近  3 sin 3 sin 4 ( ) x f x = x +  5 sin 5x + o y x −1 − 1  说明: f (x) 的情况见右图. 机动 目录 上页 下页 返回 结束

例2.设f(x)是周期为2元的周期函数，它在[-π，π) 上的表达式为 fW- -π≤x<0 3π-2π，兀 0, 0≤x<π 将f(x)展成傅里叶级数. 解-5心x-2xdx=[芝]2-月 a.-gf儿-o c cosnx l-cosnπ n nπ HIGH EDUCATION PRESS 机动目录上页下页返回结束

x −  o y 例2. 上的表达式为 将 f (x) 展成傅里叶级数. 解: − =    a f (x)d x 1 0 − = 0 cos d 1   x nx x − =    a f x nx x n ( )cos d 1 − = 0 d 1   x x  −     = 0 2 2 1 x 2  = −  −       = + 0 2 1 sin cos n nx n x nx   2 1 cos n − n = −3 −2 2 3 设 f (x) 是周期为 2 的周期函数 , 它在 机动 目录 上页 下页 返回 结束