《高等数学》课程教学资源（PPT课件）第十一章_D11_2对坐标曲线积分

第二为 第十一章 对坐标的曲我积分 一、对坐标的曲线积分的概念与性质 二、对坐标的曲线积分的计算法 三、两类曲线积分之间的联系 HIGH EDUCATION PRESS 机动

第二节 一、对坐标的曲线积分的概念与性质 二、 对坐标的曲线积分的计算法 三、两类曲线积分之间的联系 机动 目录 上页 下页 返回 结束 对坐标的曲线积分 第十一章

一、对坐标的曲线积分的概念与性质 1.引例：变力沿曲线所作的功 设一质点受如下变力作用 在xOy平面内从点A沿光滑曲线弧L移动到点B,求移 动过程中变力所作的功W 解决办法： 常力沿直线所作的功 “分割” “近似求和” “取极限” HIGH EDUCATION PRESS

一、 对坐标的曲线积分的概念与性质 1. 引例: 变力沿曲线所作的功. 设一质点受如下变力作用 在 xoy 平面内从点 A 沿光滑曲线弧 L 移动到点 B, A B L x y 求移 W  F AB cos “分割” “近似求和” “取极限” 常力沿直线所作的功 解决办法: 动过程中变力所作的功W.  F  AB A B F  F(x, y)  (P(x, y), Q(x, y)) 机动 目录 上页 下页 返回 结束

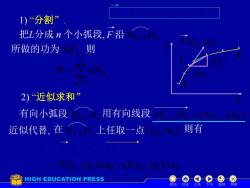
1)“分割” 把L分成n个小弧段，F沿M-M 所做的功为△，则 AW 2)近似求和” 有向小弧段 用有向线段 MM=(AXK.AYK) 近似代替，在M1上任取一点(5，)则有 =P(5k.nk)Axk +Q(5k nk )Ay HIGH EDUCATION PRESS 机动

Mk1 Mk A B x y 1) “分割”. 2) “近似求和” L 把L分成 n 个小弧段, 有向小弧段 M k1M k ( , ) k k  x y 近似代替, ( , ),  k k 则有 k k k k  P( , )x  Q( , )y  k   k  所做的功为 , Wk F 沿Mk1Mk Wk F k Mk 1Mk ( , )       k ( , ) F  k k     n k W Wk 1 则 用有向线段 Mk1Mk 在M k1M k 上任取一点 k y k x 机动 目录 上页 下页 返回 结束 F(x, y)  (P(x, y), Q(x, y))

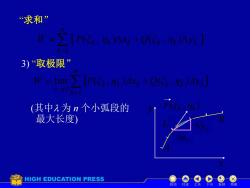
“求和” ∑[P5,Ax+0(:iA] 3)取极限” W=lim P(Ck.K )AXk +Q(CK:K )Ayk k=l (其中入为n个小弧段的 最大长度) HIGH EDUCATION PRESS 目录 返回 结

“求和” 3) “取极限”    n k W 1   k k k k k k P( , )x  Q(ξ , )y     n k W 1 0 lim    k k k k k k P(ξ , η )Δx  Q(ξ , η )Δy Mk1 Mk A B x y L ( , ) F  k k k y k x (其中 为 n 个小弧段的 最大长度) 机动 目录 上页 下页 返回 结束

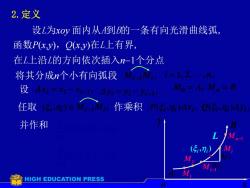
2.定义 设L为xoy面内从A到B的一条有向光滑曲线弧 函数Pxy,Q(xy)在L上有界， 在L上沿L的方向依次插入n-1个分点 将其分成n个小有向弧段-M ,i=1,2、4 设 4=-1:4=片-J-1 Mo=A,Mn=B 任取（传，7）eM 作乘积P(5,)4(,4 并作和 HIGH EDUCATION PRESS

2.定义 设L为xoy 面内从A到B的一条有向光滑曲线弧, 函数P(x,y)，Q(x,y)在L上有界, 将其分成n个小有向弧段 , Mi1Mi o x y A B Mn1 Mi Mi1 M2 M1 ( , ) i i  L 任取 ( , ) ,  i i  Mi1Mi 作乘积 ( , ) , i i i P    x 在L上沿L的方向依次插入n1个分点 i  1, 2, ,n, 设 , M0  A, Mn  B i  i  i1  x x x , i  i  i1  y y y ( , ) , i i i Q    y xi i y 并作和 ( , ) , 1 i n i  P  i i  x  ( , ) , 1 i n i i i Q     y 

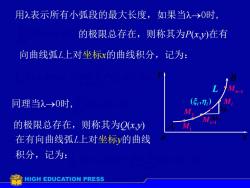
用入表示所有小弧段的最大长度，如果当入→>0时， 的极限总存在，则称其为P(xy)在有 向曲线弧L上对坐标x的曲线积分，记为： 同理当入-→0时， (5,n 的极限总存在，则称其为Qx,y) 在有向曲线弧L上对坐标y的曲线 积分，记为： HIGH EDUCATION PRESS

o x y A B Mn1 Mi Mi1 M2 M1 ( , ) i i  L xi i y 用表示所有小弧段的最大长度，如果当0时, i n i i i  P    x 1 ( , ) 的极限总存在，则称其为P(x,y)在有 向曲线弧L上对坐标x的曲线积分，记为： L P(x, y)d x i n i P  i i x      1 0 lim ( , ) 同理当0时, i n i i i Q     y 1 ( , ) 的极限总存在，则称其为Q(x,y) 在有向曲线弧L上对坐标y的曲线 积分，记为：LQ( x, y)d y i n i i i Q    y      1 0 lim ( , )

被积函数 ，Q(,)= lim ∑2(5,7)·4 积分和式 积分弧段 坐标微分 对坐标的曲线积分统称为第二类曲线积分 平面变力F(x,)=P(x,yi+(,)i 沿L所作的功 若记 则 HIGH EDUCATION PRESS

L P( x, y)d x i n i P  i i  x      1 0 lim ( , ) 对坐标的曲线积分统称为第二类曲线积分 被积函数 积分弧段  积分和式 LQ(x, y)dy lim ( , ) . 1 0      n i i i i Q    y  坐标微分 F x y P x y i Q x y j    平面变力 ( , )  ( , )  ( , ) 沿L所作的功  L  L W P(x, y)d x Q(x, y)d y    L P(x, y)d x Q(x, y)d y 简记为 若记 dr dx i dy j,      则    L W F x y dr   ( , )

几点说明： (1)所谓“对坐标的曲线积分”，有两个特征： ·积分和是在有向曲线弧L上作出的； ·积分和中的微元素是有向小弧段所对应的关于 坐标x和y的增量。 即被积表达式中的微分是关于坐标x和y的微分。 (2)当P(x,),Q(x,y)在有向光滑曲线弧L上连续， 第二类曲线积分都存在。 (3)L可以推广到分段光滑的情形：L=L1+2 HIGH EDUCATION PRESS

（1）所谓“对坐标的曲线积分” ，有两个特征： • 积分和是在有向曲线弧L上作出的； • 积分和中的微元素是有向小弧段所对应的关于 坐标x和y 的增量。 几点说明： 即被积表达式中的微分是关于坐标x和y的微分。 （2）当P (x , y) , Q (x , y)在有向光滑曲线弧L上连续， 第二类曲线积分都存在。 （3）L 可以推广到分段光滑的情形：L  L1  L2   LF x y dr   ( , )    1 ( , ) L F x y dr   L P( x, y)d x i n i P  i i  x      1 0 lim ( , )    2 ( , ) L F x y dr 

(4)推广至空间的情形 P(,y,)在空间有向曲线弧下上对坐标x的曲线积分为 同理 若记 则 HIGH EDUCATION PRESS

P(x, y,z)在空间有向曲线弧 上对坐标x的曲线积分为  P(x, y,z)dx （4）推广至空间的情形 同理  Q(x, y,z)dy lim ( , , ) . 1 0 i n i P  i i  i x       lim ( , , ) . 1 0 i n i i i i Q     y        R( x, y,z)dz i n i i i i R    z      1 0 lim ( , , )  Pd x   Qd y   Rd z      Pdx Qdy Rd z 简记为 若记 A(x, y,z) P(x, y,z)i Q(x, y,z) j R(x, y,z)k,        则 dr dx i dy j dz k,            Pdx Qdy Rd z     A x y z dr  ( , , )

3.性质 P(x,y)dx+(x,y)dy=F(x,y)dr ∫IaF)士BF(x小d =a,F(x,y在+p,F(x,y山 (2)若L可分成k条有向光滑曲线弧上，(1=1·，k) 则 P(x.y)dx+O(x.y)dy 注：第一类曲线积分中的不等式保号性质在此不成立 HIGH EDUCATION PRESS

3. 性质 (2) 若 L 可分成 k 条有向光滑曲线弧 L ( i 1, , k), i     L P(x, y)dx Q(x, y)dy     k i Li P x y x Q x y y 1 ( , )d ( , )d 则 机动 目录 上页 下页 返回 结束 1 2 (1) [ ( , ) ( , )] L  F x y   F x y dr          L L P x y dx Q x y dy F x y dr   ( , ) ( , ) ( , )       L L F x y dr F x y dr     ( , ) ( , )  1  2 注：第一类曲线积分中的不等式保号性质在此不成立