《高等数学》课程教学资源（PPT课件）第九章_D9_7方向导数与梯度

第七节 第九章 方向导数写梯袁 、 方向导数 二、梯度 三、方向导数与梯度的关系 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第九章 第七节 一、方向导数 机动 目录 上页 下页 返回 结束 二、梯度 三、方向导数与梯度的关系 方向导数与梯度

问题的提出 考虑二元函数f(x,y)的偏导数 (xo2o)=lim f(x0+Ax,0)-f(x0,y0) Ax→0 △x 反映函数在水平方向上的变化率。 M(xo+△x,Jo) ◆←◆ 偏导数f(x0,0) Mo(xo-Yo) 反映函数在垂直方向上的变化率。 在实际问题中，还需要考虑函数在任意方向上的变 化率问题，如冷热空气的流动，温度场的变化等。 等HIGH EDUCATION PRESS

问题的提出 考虑二元函数 z=f (x,y) 的偏导数 反映函数在水平方向上的变化率。 偏导数 反映函数在垂直方向上的变化率。 在实际问题中，还需要考虑函数在任意方向上的变 化率问题，如冷热空气的流动，温度场的变化等。•

方向导数的定义 函数在某一方向上的变化率，称为函数在该方向 上的方向导数。 f(x,y)在点处沿方向1的方向导数。 与同方向的单位向量为e1=(cosa,cs),设|PR|=t, 则射线1的参数方程为 x=x+tcosa (x,y ly yo +tcos B 动点从P到P时函数的增量 P(x0,y0） △=f(x,Jy)-f(x0,0) f(xo+tcosa,yo+tcosB)-f(xo,yo) HIGH EDUCATION PRESS

一、方向导数的定义 o y x l • 函数在某一方向上的变化率，称为函数在该方向 上的方向导数。 与l同方向的单位向量为 则射线 l 的参数方程为 | | , 0 设 PP = t • P( x, y) t  ( , ) 0 0 0 P x y     = + = +   cos cos 0 0 y y t x x t 动点从 P0 到P 时函数的增量 ( , ) ( , ) 0 0  z = f x y − f x y ( cos , cos ) ( , ) 0 0 0 0 = f x + t  y + t  − f x y ➢ z=f ( x , y ) 在点 处沿方向 l 的方向导数

函数在I方向上的增量与PP,=t的比值 (函数在方向上的平均变化率) P(x,y f(xo+tcosa,yo+tcosB)-f(xo,yo) t P6(x0,Jy0) 令P→，即t→0*，如果极限 lim f(xo+tcosa,yo+tcosB)-f(xo,Yo) 存在 t-→0+ t 则称它为f(x,y)在点处沿方向1的方向导数。 记为af lim f(xo+tcosa,o+tcosB)-f(xo,Yo) (x0%)t→0* t HIGH EDUCATION PRESS

函数在 l 方向上的增量 它与| PP0 |= t 的比值 = t z （函数在l方向上的平均变化率） 如果极限 存在 t f ( x t cos , y t cos ) f ( x , y ) 0 +  0 +  − 0 0 , 令 P → P0 0 , → + 即 t t f x t y t f x y t ( cos , cos ) ( , ) lim 0 0 0 0 0 + + − → +   o y x l • • P( x, y) t  ( , ) 0 0 0 P x y  则称它为 f ( x , y ) 在点 处沿方向 l 的方向导数。 记为

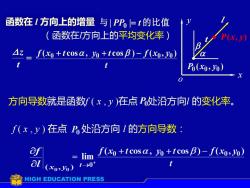
函数在1方向上的增量与|PP=t的比值 (函数在方向上的平均变化率) △z f(xo+tcosa,yo+tcosB)-f(xo,Yo) 6(x0,J0 方向导数就是函数f(x,y)在点处沿方向1的变化率。 f(x,y)在点P处沿方向1的方向导数： lim f(xo+tcosa,o+tcos B)-f(xo,yo) al (xo>Yo)t0* HIGH EDUCATION PRESS

函数在 l 方向上的增量 它与| PP0 |= t 的比值 = t z （函数在l方向上的平均变化率） t f ( x t cos , y t cos ) f ( x , y ) 0 +  0 +  − 0 0 o y x l • • P( x, y) t  ( , ) 0 0 0 P x y  f ( x , y ) 在点 处沿方向 l 的方向导数： 方向导数就是函数f ( x , y )在点 P0 处沿方向l 的变化率

> 总结 (1) 二元函数f(x,y在P(xo,Jy)沿方向1（方向角为&，） 的方向导数为 of lim f(x+tcosa,yo+tcosB)-f(xo,Yo) al (xo,yo) t→0 (2) 三元函数f(x,y,z)在P,(x,J,)沿方向1的方向导数 of lim f(xo+tcosa,yo+tcosB,to+tcosy)-f(xo,yo,Zo) al (xo,yo,) t 单侧极限 分子：射线上两点函数值之差 (3)定义式的特点 比式 分母：射线上两点的距离 实质：函数在方向上的变化率

t f x t y t z t f x y z t ( cos , cos , cos ) ( , , ) lim 0 0 0 0 0 0 0 + + + − = → +    ( , , ) 0 0 0 l x y z f   ➢ 总结 二元函数 f (x, y) 在 ( , ) 0 0 0 P x y 沿方向l (方向角为 ,  ) 的方向导数为 t f x t y t f x y t ( cos , cos ) ( , ) lim 0 0 0 0 0 + + − = → +   ( , ) 0 0 l x y f   (1) (2) 三元函数 f (x, y,z) 在 ( , , ) 0 0 0 0 P x y z 沿方向 l 的方向导数 (3) 单侧极限 定义式的特点 比式 分子: 射线l上两点函数值之差 分母: 射线l上两点的距离 实质：函数在方向l上的变化率

定理如果函数f化，y)在点P0(x0,y0可微分，那么函数在 该点沿任一方向1的方向导数存在，且有 af a\(xo) =fx(xoYo)cosa+fy(xo,o)cosB 其中cosa,cosB是方向l的方向余弦， 定理推广：若函数f(x,y,)在点P(x,y,)处可微， 则函数在该点沿任意方向1的方向导数存在，且有 f_∂ cosa+- 其中a,B,y为1的方向角. HIGH EDUCATION PRESS

定理 如果函数 f (x,y)在点 可微分，那么函数在 该点沿任一方向 l 的方向导数存在，且有 其中 cos, cos  是方向 l 的方向余弦. ( , ) 0 0 0 P x y ( , )cos ( , )cos (2) 0 0 0 0 ( , ) 0 0 f x y  f x y  l f x y x y = +   定理推广: 若函数 f (x, y,z) 在点 P(x, y,z) 处可微 , 则函数在该点沿任意方向l 的方向导数存在 , cos cos  cos z f y f x f l f   +   +   =   且有

例1.求函数z=xe2y在点P(1,0)处沿从点P(1,0)到 点Q(2,-1)的方向的方向导数 解：方向1即向量P式=L,-1的方向， 与1同向的单位向量 (322 0x(L,0) =1 (1,0) 2xe2x 02 所求方向导数为 1.1 √2 alla.o) *2(2 2 HIGH EDUCATION PRESS

例1. 求函数 在点 P (1,0) 处沿从点 P (1,0) 到 点Q (2,−1) 的方向的方向导数. y z x 2 = e =   (1,0) y z 2 e 2, (1,0) 2 = y x 解: 方向 l 即向量 的方向， 与 l 同向的单位向量 . 2 1 , 2 1       el = − PQ = (1,−1) 2 2 ) 2 1 2 ( 2 1 1 (1,0) =  +  − = −   l z 所求方向导数为 =   (1,0) x z 因为函数可微分，且 e 1, (1,0) 2 = y

例2.求函数1=x2yz在点P(1,1,1)沿向量7=(2，-1， 3)的方向导数 解：向量7的方向余弦为 2 3 cosa= cosy= 14 8-(a:+yi01》 /14 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 求函数 在点 P(1, 1, 1) 沿向量 3) 的方向导数 .    =    l P u 14 2 2xyz    +  14 2 3 x y 机动 目录 上页 下页 返回 结束 解: 向量 l 的方向余弦为

例3.求函数z=3x2y-y2在点P(2,3沿曲线y=x2-1 朝x增大方向的方向导数， 解：将已知曲线用参数方程表示为 x=x 它在点P的切向量为1,2x)x=2=(（1,4) 12 4 17 cos B=7 周，m市*6x2-2]e9 HIGH EDUCATION PRESS 机动目 下页返回结束

例3. 求函数 在点P(2, 3)沿曲线 朝 x 增大方向的方向导数. 解: 将已知曲线用参数方程表示为 2 (1, 2 ) x= 它在点 P 的切向量为 x , 17 1  cos = 17 60 = o x y 2 P    = − = 1 2 y x x x = (1, 4) 17 4 cos  = −1 机动 目录 上页 下页 返回 结束