《高等数学》课程教学资源（PPT课件）第八章_8-6空间曲线及其方程

第之节 第八章 空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第八章 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影 第六节 机动 目录 上页 下页 返回 结束 空间曲线及其方程

一、空间曲线的一般方程 空间曲线可视为两曲面的交线，其一般方程为方程组 F(x,y,2)=0 G(x,y,2)=0 (x,y=0 例如，方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C HIGH EDUCATION PRESS 下页返回结束

一、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 L G(x, y,z) = 0 F(x, y,z) = 0 1 S 例如,方程组 表示圆柱面与平面的交线 C. x z 1 y o C 2 机动 目录 上页 下页 返回 结束

又如方程组 =Va-x- y= 表示上半球面与圆柱面的交线C HIGH EDUCATION PRESS 机动目录上页下页返回结束

又如,方程组 表示上半球面与圆柱面的交线C. y x z a 机动 目录 上页 下页 返回 结束

二、空间曲线的参数方程 将曲线C上的动点坐标x,y表示成参数1的函数： x=x(t) 空间曲线的 参数方程 y=y(t) Z=Z(t) 例如，圆柱旋线的参数方程为 x=acosot y =asinot 令0=0t,b= x=acos z=vt y=asine z=b0 当0=2π时，上升高度h=2πb,称为螺距 HIGH EDUCATION PRESS 机动目录上页下页返回结束

z x y o 二、空间曲线的参数方程 将曲线C上的动点坐标x, y, z表示成参数t 的函数: 空间曲线的 参数方程 例如,圆柱螺旋线    v 令 = t , b = h = 2 b 的参数方程为 上升高度 , 称为螺距 .  M 机动 目录 上页 下页 返回 结束

例1.将下列曲线化为参数方程表示： (2 解：(1)根据第一方程引入参数，得所求为 x=coSt y=sint (0≤t≤2π) z=号(6-2cost) 2)将第二方程变形为（心x-)+y2=,故所求为 x=号+号cos7 y= 号sint (0≤t≤2π) z=a cost HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 将下列曲线化为参数方程表示: 解: (1) 根据第一方程引入参数 , (2) 将第二方程变形为 故所求为 得所求为 机动 目录 上页 下页 返回 结束

三、空间曲线在坐标面上的投影 空间曲线C的一般方程 F(x,y,z)=0 C G(x,y,z)=0 准线 消去得 H(x,y)=0 柱面 HIGH EDUCATION PRESS

三、空间曲线在坐标面上的投影 空间曲线C的一般方程 C： 消去 z 得 柱面 准线

三、空间曲线在坐标面上的投影 投影柱面与投影（曲线） 投影柱面 以空间曲线C为准线、母线平行 于轴的柱面叫做曲线C关于xOy面的 投影柱面： 投影柱面与xOy面的交线叫做曲 线C在xOy面上的投影曲线，或简称投 投影曲线 影 类似地可以定义曲线C在其它坐 标面上的投影 HIGH EDUCATION PRESS

投影柱面与xOy面的交线叫做曲 线C在xOy面上的投影曲线, 或简称投 影. 类似地可以定义曲线C在其它坐 标面上的投影. ❖投影柱面与投影(曲线) 以空间曲线C为准线、母线平行 于z轴的柱面叫做曲线C关于xOy面的 投影柱面. 投影柱面 投影曲线 三、空间曲线在坐标面上的投影

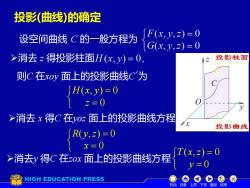
投影（曲线）的确定 设空间曲线C的一般方程为 F(x,y,z)=0 G(x,y,z)=0 >消去z得投影柱面H(x,y)=0, 投影柱面 则C在xoy面上的投影曲线C为 H(x,y)=0 z=0 >消去x得C在yoz面上的投影曲线方程 投影曲线 R(y,2)=0 1x=0 >消去y得C在zox面上的投影曲线方程 T(x,2)=0 0y=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

投影(曲线)的确定 设空间曲线 C 的一般方程为 ➢消去 z 得投影柱面 则C 在xoy 面上的投影曲线C´为 ➢消去 x 得C 在yoz 面上的投影曲线方程 ➢消去y 得C 在zox 面上的投影曲线方程    = = 0 ( , ) 0 z H x y    = = 0 ( , ) 0 x R y z    = = 0 ( , ) 0 y T x z 机动 目录 上页 下页 返回 结束 投影柱面 投影曲线

例4 x2+y2+22=1 在xoy面上的投影曲线方程为 步骤 +2262=0 2=0 HIGH EDUCATION PRESS DeOC8 机动目录上页下页返回结束

z y x C 1 o 例4 在 xoy 面上的投影曲线方程为    = + − = 0 2 2 0 2 2 z x y y    + − + − = + + = ( 1) ( 1) 1 1 : 2 2 2 2 2 2 x y z x y z C 机动 目录 上页 下页 返回 结束 步骤

例5 上半球面z=√4-x2-y2 和锥面 z=3(x2+y2) 所围的立体在xoy面上的投影区域为： 二者交线在 xoy面上的投影曲线所围之域.步骤 二者交线 在xoy面上的投影曲线 z=0 所围圆域：x2+y2≤1，z=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

z x y o 1 C 例5 所围的立体在 xoy 面上的投影区域为: 上半球面 和锥面 在 xoy 面上的投影曲线 二者交线 1, 0. 2 2 所围圆域: x + y  z = 二者交线在 xoy 面上的投影曲线所围之域 . 机动 目录 上页 下页 返回 结束 步骤