《高等数学》课程教学资源（PPT课件）第八章_8-5曲面及其方程

第三节 第八章 曲面及其方程 一、 曲面研究的基本问题 二、 旋转曲面 三、柱面 四、二次曲面 HIGH EDUCATION PRESS D0C⊙8 机动目录上页下页返回结束

四、二次曲面 第三节 一、曲面研究的基本问题 二、旋转曲面 三、柱面 机动 目录 上页 下页 返回 结束 曲面及其方程 第八章

一、曲面研究的基本问题 两个基本问题： (1)已知一曲面作为点的几何轨迹时， 建立这曲面的方程 F(x,y,z)=0 (2)已知坐标x,y,满足的方程时 研究这方程所表示的曲面的形状 (必要时需作图) HIGH EDUCATION PRESS 机动目 录上页下页返回结束

F(x, y,z) = 0 S z y x o 两个基本问题 : (1) 已知一曲面作为点的几何轨迹时, 建立这曲面的方程. (2) 已知坐标 x, y, z满足的方程时 , 研究这方程所表示的曲面的形状. ( 必要时需作图 ) 机动 目录 上页 下页 返回 结束 一、曲面研究的基本问题

例1.建立球心在点Mo(xo,yo,zo)半径为R的 球面的方程 解：设M(x,y,)是球面上任一点，则 MoM=R 即 V(x-x0)2+0y-%)2+(2-)2=R 故所求方程为 (x-)2+(y-%)2+(E-20)》2=R2 特别，当M在原点时，球面方程为 x2+y2+z2=R2 HIGH EDUCATION PRESS 机动目录上页下页返回结束

解: 设 是球面上任一点， 故所求方程为 例1. 建立球心在点 、 球面的方程. 特别,当M0在原点时,球面方程为 即 则 半径为 R的 x y z o M M0 x − x + y − y + z − z = R 2 0 2 0 2 0 ( ) ( ) ( ) 2 2 0 2 0 2 0 (x − x ) + (y − y ) + (z − z ) = R 2 2 2 2 x + y + z = R 机动 目录 上页 下页 返回 结束

例2.研究方程x2+y2+z2-2x+4y=0表示怎样 的曲面 解：配方得 (x-1)2+(0y+2)2+z2=5 此方程表示： 球心为M(1,-2,0) 半径为√5的球面！ 说明：如下形式的三元二次方程(A≠0) A(x2+y2+z2)+Dx+E+F2+G=0 都可通过配方研究它的图形 其图形可能是一个球面，或点，或虚轨迹 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 研究方程 解: 配方得 5 (1, 2, 0), 此方程表示: M0 − 说明: 如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形. 其图形可能是 的曲面. 表示怎样 半径为 的球面. 球心为 一个球面 , 或点 , 或虚轨迹. 机动 目录 上页 下页 返回 结束

二、旋转曲面 定义2.一条平面曲线绕其平面上一条定直线旋转 周所形成的曲面叫做旋转曲面. 定直线称为轴；旋转曲线称为母线. 例如： HIGH EDUCATION PRESS D◆0C08 机动目录上页下页返回结束

定义2. 一条平面曲线 二、旋转曲面 绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 定直线称为轴； 旋转曲线称为母线. 例如 : 机动 目录 上页 下页 返回 结束

建立y0z面上曲线C:f(y,z)=0绕z轴旋转所成 旋转曲面的方程： 设M(x,y,)为曲面上任一点，它是曲线C上 点M(0,y,)绕z轴旋转而得到的.因此有如下关 系等式： f(1,)=0 z=21, M(0,y,） M(x/y, 故旋转曲面方程为 f(±Vx2+y2,)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

➢ 建立 yoz面上曲线C: 绕 z 轴旋转所成 旋转曲面的方程: 故旋转曲面方程为 f (y1 ,z1 ) = 0 (0, , ) 1 1 1 M y z 1 M (x, y,z) 2 2 1 z = z , x + y = y ( , ) 0 2 2 f  x + y z = f (y,z) = 0 o z y x C 机动 目录 上页 下页 返回 结束 设 M (x, y, z) 为曲面上任一点, 它是曲线 C上 点M1 (0, y1 , z1 )绕 z 轴旋转而得到的. 因此有如下关 系等式：

思考：当曲线C绕y轴旋转时，方程如何？ C:f(y,z)=0 f(y,±Vx2+z2)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

思考：当曲线 C 绕 y 轴旋转时，方程如何？ C : f (y,z) = 0 o y x z ( , ) 0 2 2 f y  x + z = 机动 目录 上页 下页 返回 结束

例3.试建立顶点在原点，旋转轴为z轴，半顶角为α 的圆锥面方程 解：在0z面上直线L的方程为 z=ycota 绕Z轴旋转时，圆锥面的方程为 M(0,y,2) z=±Vx2+y2cota 令a=cota 两边平方 22=a2(x2+y2) HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 试建立顶点在原点, 旋转轴为 z 轴, 半顶角为 的圆锥面方程. 解: 在yoz面上直线L 的方程为 绕z 轴旋转时,圆锥面的方程为 ( ) 2 2 2 2 z = a x + y x y z  两边平方 L M (0, y,z) 机动 目录 上页 下页 返回 结束

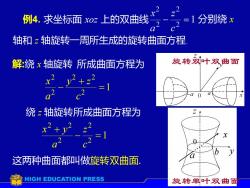
例4.求坐标面x0z上的双曲线 2 x2 2-2 =1分别绕x 轴和z轴旋转一周所生成的旋转曲面方程 解：绕x轴旋转所成曲面方程为 旋转奴叶双曲面 x2y2+2 a 绕z轴旋转所成曲面方程为 x2+y22 二1 这两种曲面都叫做旋转双曲面： HIGH EDUCATION PRESS 旋转单叶双曲面

例4. 求坐标面 xoz 上的双曲线 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 解:绕 x 轴旋转 1 2 2 2 2 2 = + − c y z a x 绕 z 轴旋转 1 2 2 2 2 2 − = + c z a x y 这两种曲面都叫做旋转双曲面. 所成曲面方程为 所成曲面方程为 机动 目录 上页 下页 返回 结束 x 旋转双叶双曲面 旋转单叶双曲面

三、柱面 引例.分析方程x2+y2=R2表示怎样的曲面 分析：在x0y面上，x2+y2=R2表示圆C, 在圆C上任取一点M1(x,y,O),过此点作 平行z轴的直线1，对1上任意点M(x,y,) 的坐标也满足方程x2+y2=R2 这说明直线1一定在x2+y2=R表示的曲面上， 即沿曲线C平行于z轴的一切直线都在曲面上 因此这个曲面可以看成是由平行于z轴的直线1 沿xOy面上的圆x2+2=2移动而形成的 x2+y2=R2表示圆柱面 HIGH EDUCATION PRESS 机动目 下页返回结

x y z 三、柱面 引例. 分析方程 表示怎样的曲面 . 的坐标也满足方程 分析:在 xoy 面上， 表示圆C, 2 2 2 x + y = R 即 沿曲线C平行于 z 轴的一切直线都在曲面上. 2 2 2 x + y = R 过此点作 平行 z 轴的直线 l ,对 l上任意 表示圆柱面 C o 在圆C上任取一点 ( , ,0), 1 M x y l M M1 点M (x, y,z) 机动 目录 上页 下页 返回 结束 这说明直线l 一定在x 2+y 2=R2表示的曲面上， 因此这个曲面可以看成是由平行于 z 轴的直线 l 沿 xOy 面上的圆 x 2+y 2=R2 移动而形成的