《线性代数》课程PPT教学课件（B）第五章 相似矩阵与二次型_5-4实对称矩阵的相似对角形

§5.4实对称矩阵的相似对角形 一、实对称矩阵的性质 二、实对称矩阵的对角化 三、小结

§5.4 实对称矩阵的相似对角形 一、实对称矩阵的性质 二、实对称矩阵的对角化 三、小结

一、实对称矩阵的性质 上节讨论了一般方阵与对角形矩阵的相似问题， 现在我们来解决本章的主要问题，即如何用正交 矩阵使实对称矩阵与对角矩阵相似为此，我们 首先证明下面三个引理。 引理5.4.1实对称矩阵的特征值为实数 证明设复数为对称矩阵4的特征值，复向量x为 对应的特征向量， 即 Ax=入x,x≠0. 用九表示的共轭复数，x表示x的共轭复向量， 则 Ax=Ax=(Ax)=(几x)=元x

引理5.4.1 实对称矩阵的特征值为实数. , 证明 , 设复数为对称矩阵A x 的特征值 复向量 为 对应的特征向量 即 Ax = x , x  0. 用 表示的 共轭复数 , 则 Ax = Ax = = = ( ) ( ) . Ax x x   x表示x的共轭复向量 , 一、实对称矩阵的性质 上节讨论了一般方阵与对角形矩阵的相似问题， 现在我们来解决本章的主要问题，即如何用正交 矩阵使实对称矩阵与对角矩阵相似.为此，我们 首先证明下面三个引理

于是有'Ax='(Ax)='x=x, 另外'Ax=A'x=(A)'x=(2x)'x=元xx 两式相减，得(2-元)x=0. 但因为x≠0， 所以=∑x=∑x≠0，→（亿-元）=0， 即2=元，由此可得是实数

于是有 = ( ) Ax x = ( )  x x   x x  = 两式相减，得 ( ) 0.   − = x x  但因为x  0,  − = ( ) 0,   即 = , 由此可得是实数. 2 1 1 0, n n i i i i i x x x x x = = 所以  = =    x Ax x Ax   = ( ) = x x  =  x x  , 另外 x Ax x A x    =

由定理5.4.1可推出： 由于对称矩阵4的特征值2为实数，所以齐次 线性方程组 (A-九E)x=0 是实系数方程组，由A-2,E=0知必有实的基础解 系，从而对应的特征向量为实向量 引理5.4.2实对称矩阵的不同特征值的特征向量是正 交的

由定理5.4.1可推出： , ( ) 0 , 0 , . i i i A A E x A E    − = − = 由于对称矩阵 的特征值 为实数 所以齐次 线性方程组 是实系数方程组 由 知必有实的基础解 系 从而对应的特征向量为实向量 引理5.4.2 实对称矩阵的不同特征值的特征向量是正 交的

证明 设P1,P,是对称矩阵A的不同的两个特征值 2,入，的特征向量，即 Ap1=元P1,Ap2=入2P2, .A=A', ∴p1'=(2,=(4py=p1'A=p1'A 于是 P1P2=p1'Ap2=p'(P)=九2P1P2, →(21-2p1p2=0. 入≠22，∴.P1P2=0.即p1与p2正交

1 2 1 2 , , , p p A   设 是对称矩阵 的不同的两个特征值 的特征向量 即 证明 1 1 1 2 2 2 Ap p Ap p = =   , ， A A =  , 1 1  p  1 1 p A p A,   = =  于是 1 1 2  p p  = 2 1 2  p p , =  1 2 1 2  − = ( ) 0.   p p  , 1  2 .  = p p 1 2  0. 即p1与p2正交 1 2 p Ap  1 2 2 = p p  ( )  1 1 = ( )  p  1 = ( ) Ap 

引理5.4.3设A为阶对称矩阵，是A的特征方程的 r重根，则矩阵A一九E的秩为-r,从而对应特征值入 恰有r个线性无关的特征向量. 定理5.4.1设A为阶实对称矩阵，则有正交矩阵P, 使PAP=人，其中人是以A的个特征值为对角元 素的对角矩阵。 证明设4的的互不相等的特征值为2，入2，.，入， 它们的重数依次为，2，.，(+2+.+r=)

1 5.4.1 , , , . A n P P AP A n − =   设 为 阶实对称矩阵 则有正交矩阵 使 其中 是以 的 个特征值为对角元 素的对 定 角矩阵 理 证明 1 2 , , , , 设A的的互不相等的特征值为  s 1 2 1 2 , , , ( ). s s 它们的重数依次为r r r r r r n + + + = , , 5.4.3 , . A n A r A E n r r  − −   设 为 阶对称矩阵 是 的特征方程的 重根 则矩阵 的秩为 从而对应特征值 恰有 个线性无关的特 引 征向量 理

根据引理5.4.1（对称矩阵的特征值为实数）和引理 5.4.3(如上)可得： 对应的特征值2(i=1,2,.,S)恰有线性无关的实特征 向量，把它们正交化并单位化，即得个单位正交的特 征向量，并由+.+=n,可知，这样的特征向量共有 n个. 由引理5.4.2知对应于不同特征值的特征向量正交，故 这n个单位特征向量两两正交. 以它们为列向量构成正交矩阵P,则 P-1AP=P-PΛ=A

根据引理5.4.1(对称矩阵的特征值为实数)和引理 5.4.3( 如上)可得： 由引理5.4.2知对应于不同特征值的特征向量正交,故 这n个单位特征向量两两正交. 以它们为列向量构成正交矩阵P，则 =  =  − − P AP P P 1 1 . , , , , , ( 1,2, , ) 1 个 征向量 并由 可知 这样的特征向量共有 向量 把它们正交化并单位化 即得 个单位正交的特 对应的特征值 恰有线性无关的实特征 n r r n r i s s i i + + = =   

其中对角矩阵A的对角元素含个，.，个2，恰 是A的n个特征值. 二、实对称矩阵对角化的方法 根据上述结论，利用正交矩阵将对称矩阵化 为对角矩阵，其具体步骤为： 1.求A的特征值 2由(A-2,E)x=0,求出4的特征向量； 3将特征向量正交化； 4.将特征向量单位化. 5.以特征向量为列向量写出正交矩阵

根据上述结论，利用正交矩阵将对称矩阵化 为对角矩阵，其具体步骤为： 3.将特征向量正交化; 4.将特征向量单位化. 2. ( ) 0, ; 由 A E x A − = i 求出 的特征向量 二、实对称矩阵对角化的方法 5.以特征向量为列向量写出正交矩阵. 1.求A的特征值 1 1 , , , . s s r r A n 其中对角矩阵的对角元素含 个  个 恰 是 的 个特征值

40 0 例1设A= 0 31,求正交矩阵P,使P-1AP 0 13 为对角形矩阵。 解()第一步求A的特征值 4-元 0 0 A-E= 0 3-1 =(2-2)(4-2)2, 0 1 3-元 得特征值21=2，入2=几3=4

    − − − − = 0 1 3 0 3 1 4 0 0 A E 2 = − − (2 )(4 ) ,   2, 4. 得特征值 1 = 2 = 3 = 1 4 0 0 1 0 3 1 0 1 3 . A P P AP −     =       例 设 ，求正交矩阵 ，使 为对角形矩阵 解 (1)第一步 求A的特征值

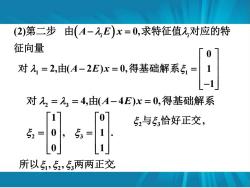
(2)第二步由(A-,E)x=0,求特征值2，对应的特 征向量 0 对人，=2，由(A-2E)x=0,得基础解系51= -1 对人2=2=4，由(A-4E)x=0,得基础解系 1 0 52与53恰好正交， 52= 所以5,52,5两两正交

(2) 0, 第二步 由( A E x − =   i i ) 求特征值 对应的特 征向量 1 1 0 2, ( 2 ) 0, 1 1   A E x     = − = =       − 对 由 得基础解系 2 3 2 3 4, ( 4 ) 0, 1 0 0 1 , . 0 1   A E x   = = − =         = =             对 由 得基础解系 ,  2与 3恰好正交 , , . 所以 1  2  3两两正交