《线性代数》课程教学课件（PPT讲稿，B）第一章 n阶行列式_1.2 n阶行列式的性质

线性代数 山东理工大学

线性代数 山东理工大学

第1章n阶行列式 §1.2n阶行列式的性质

§1.2 n阶行列式的性质 第1章 n阶行列式

定理1.2.1：阶行列式等于它的任意一行（列）的各元素与其 对应的代数余子式的乘积之和，即 D=u1A1+a2A2+L+mAn,(i=1,2,L,n), 或 D=41A+a2jA2j+L+0nA,(0=1,2,L,n): 这个定理也称为行列式展开定理。 推论：如果阶行列式中第行所有元素除外都为零，那 么行列式就等于a与其对应的代数余子式的乘积， 即 D=ajAi

定理1.2.1：n阶行列式等于它的任意一行(列)的各元素与其 对应的代数余子式的乘积之和，即 1 1 2 2 ,( 1,2, , ). D a A a A a A j n = + + + = j j j j nj nj L L 或 1 1 2 2 ,( 1,2, , ), D a A a A a A i n = + + + = i i i i in in L L . ijAij D = a 推论： ij a 如果n阶行列式中第i行所有元素除 外都为零，那 么行列式就等于 与其对应的代数余子式的乘积， 即 ij a 这个定理也称为行列式展开定理

行列式的性质 11 L12 L ain 设 D L21 L22 a2n M M M M an2 L D'(D)= 2M 称为D的转置行列式 M M M 02 L nn

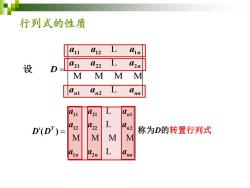
行列式的性质 11 12 1 21 22 2 1 2 n n n n nn a a a a a a D a a a = L L M M M M L 设  = L L M M M M L 11 21 1 12 22 2 1 2 ( ) n T n n n nn a a a a a a D D a a a 称为D的转置行列式

性质1.2.1：行列式与它的转置行列式相等，即D=D。 证明：用数学归纳法。 当=2时， 11 21 结论成立。 L21 L22 12 L22 假设对n-1阶行列式结论成立，对于n阶行列式D和DT, 分别按第一行和第一列展开 421L42-14HL4n n-24,豆a,(e M M, an L ag-i L am

假设对n-1阶行列式结论成立，对于n阶行列式D和 ， 分别按第一行和第一列展开 T D 21 2 1 2 1 2 1 1 1 1 1 1 1 1 1 1 ( 1) ( 1) , j j n n n j j j j j j j n nj nj nn a a a a D a M a a a a a − + + + = = − + = − = −   L L M L M M L L 证明：用数学归纳法。 当n=2时， 11 12 11 21 ，结论成立。 21 22 12 22 a a a a a a a a = 性质1.2.1：行列式与它的转置行列式相等, 即 D D= T

21 L an L M M M L m=2a-w,2a- 02j- Aj-1 L -1 02j+1 L Qj+1 L j+1 M M M L 由于M,和M,是m1阶行列式，且M是M,的转置行列式， 根据假设M,=M于是D=D'. 在行列式中，行和列的位置是对称的，对行成立的，对列也成立

21 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 ( 1) ( 1) . i n n n j ij nj T j j j j j j j j ij nj n in nn a a a a a a D a M a a a a a a a − − − + + = = + + + = − = −    L L M M M L L L L M M M L L 由于 和 是n-1阶行列式，且 是 的转置行列式， 根据假设 ，于是 M1 j M1 j M1 j  M1 j  M M 1 1 j j =  . T D D = 在行列式中,行和列的位置是对称的,对行成立的,对列也成立

例如上三角行列式 12 L 0 L22 L D 2 M M M 0 0 L Ann 由定理1.2.1的推论即得 0 L 0 0 D=DT= ap 02L M M M ain A2n L

11 12 1 22 2 0 . 0 0 n n nn a a a a a D a = L L M M M L 例如上三角行列式 11 12 22 11 22 1 2 0 0 0 . T nn n n nn a a a D D a a a a a a = = = L L L M M M L 由定理1.2.1的推论即得

性质1.2.2：互换行列式的两行（列)，行列式的值变号。 证明： 12 M M M M an 12 L n 设D= M M MM 交换1、s两行，得 as 0s2 L asn Az L Ajn M M M M M M M M an Qn2 L ast 02 L Agn →行 D=M M M M an L12 L 4n→s行 M M M M 则D=-D an2 L

性质1.2.2：互换行列式的两行（列），行列式的值变号。 证明： 设 11 12 1 1 2 1 2 1 2 n l l ln s s sn n n nn a a a a a a D a a a a a a = L M M M M L M M M M L M M M M L 交换l、s 两行，得 11 12 1 1 2 1 1 2 1 2 n s s sn l l ln n n nn a a a a a a D a a a a a a = L M M M M L M M M M L M M M M L → l行 → s行 1 则 . D D = −

证明：用数学归纳法。 411 L12 L21 当=2时， 结论成立。 L2 L22 假设对-1阶行列式结论成立，对于阶行列式，分别将D和D 按第行展开(i≠s,1),得 D=立4，-IM,D=2a,-1N, 其中Mn和N分别为D和D,中元素M,的余子式，并且N是由M 互换两行得到的-1阶行列式，由归纳假设M,=-N,因此有 D=-D. 记法 行列式的第行：T 交换s、t两行：r←分 行列式的第s列：C 交换s、t两列：C,今C

1 1 1 ( 1) , ( 1) , n n i j i j ij ij ij ij j j D a M D a N + + = = = − = −   证明：用数学归纳法。 当n=2时， ，结论成立。 11 12 21 22 21 22 11 12 a a a a a a a a = − i s l  , 假设对n-1阶行列式结论成立，对于n阶行列式，分别将D和 按第i行展开（ ），得 D1 其中 和 分别为D和 中元素 的余子式，并且 是由 互换两行得到的n-1阶行列式，由归纳假设 ，因此有 Mij ij D1 N ij a Nij Mij M N ij ij = − 1 D D = − . 记法 行列式的第s行： s r 行列式的第s列： s c 交换s、t两行： s t r r  交换s、t两列： s t c c 

推论：如果行列式有两行（列)相同，则行列式为0。 性质1.2.3：用数k乘行列式的某一行（列)中所有元素， 等于用数k乘此行列式。 011 12 L L12 L M M M M M M M M kas kay2 L =k as as2 L M M M M M M M M Ani an2 L Ann anl an2 L Ann 推论1： 行列式中某一行（列)的公因子可以提到行列式符 号外面。 记法第s行乘以k:kr 第s列乘以k:kc 推论2：若行列式有两行（列）的对应元素成比例，则行列式 等于0

推论：如果行列式有两行（列）相同，则行列式为 0 。 性质1.2.3：用数 k 乘行列式的某一行（列）中所有元素， 等于用数 k 乘此行列式。 推论1：行列式中某一行（列）的公因子可以提到行列式符 号外面。 记法 第s行乘以k： s kr 第s列乘以k: s kc 推论2：若行列式有两行（列）的对应元素成比例，则行列式 等于0 。 11 12 1 11 12 1 1 2 1 2 1 2 1 2 n n s s sn s s sn n n nn n n nn a a a a a a ka ka ka a a a k a a a a a a = L L M M M M M M M M L L M M M M M M M M L L