《线性代数》课程教学课件（PPT讲稿，B）第一章 n阶行列式_1.3 n阶行列式的计算

线性代数 山东理工大学

线性代数 山东理工大学

第1章n阶行列式 §1.3n阶行列式的计算 利用行列式按行（列）展开的定理和行列式的性质来计 算行列式，所涉及的方法主要有： 1、降阶法；2、化为三角行列式；3、拆行拆列法： 4、加边法；5、递推法；6、数学归纳法

§1.3 n阶行列式的计算 第1章 n阶行列式 利用行列式按行(列)展开的定理和行列式的性质来计 算行列式，所涉及的方法主要有： 1、降阶法；2、化为三角行列式；3、拆行拆列法； 4、加边法；5、递推法；6、数学归纳法

1、降阶法 通过第二节性质5将行列式展成某一行（列）只保存一个非零 元素，然后利用第二节定理推论，降阶计算行列式的值， 这是计算行列式常用的方法之一. 2 -1 3 2) 3 -1 2 例1计算行列式D= -1 1 1 0 0 1 -2 1 解： 1 2-1 U 12 -1 n-2n 0 -1 1 -4 3+斯0 -1 1 -4 D -1 1 0 0 3 0 3 0 1 -2 1 0 1 -2 1

例1 计算行列式 . 0 1 2 1 1 1 1 0 2 3 1 2 1 2 1 3 − − − − D = 0 1 2 1 1 1 1 0 0 1 1 4 1 2 1 3 2 1 2 − − − − − = r − r D 解: 0 1 2 1 0 3 0 3 0 1 1 4 1 2 1 3 3 1 − − − − = r +r 1、降阶法 通过第二节性质5将行列式展成某一行（列）只保存一个非零 元素，然后利用第二节定理1推论，降阶计算行列式的值， 这是计算行列式常用的方法之一

-4 -1 1 -3 1 -3 3 0 3 =18. 1-2 1-2 -20 0 例2计算行列式 b a a+b a+b+c a+b+c+d D 0 a+b a+b+c 0 0 a+b 解 a b d aa+b a+b+c 2-0 -6 a+b+c D =aa a+b a+b+c =0 0 a+b a+b+c 0 a+b 0 a+b

a a b a a b a b c a a b a b c a b c d a b c d D + + + + + + + + + + = 0 0 0 例2 计算行列式 a a b a a b a b c a a b a b c a b c d D r r + + + + + + + = − 0 0 0 2 1 0 解 = 0. 0 a a b a b c a a a b a b c a a b + + + = + + + + 1 2 1 3 0 3 1 1 4 − − − = 1 2 0 3 0 0 1 1 3 3 1 − − − = c −c 18. 2 0 1 3 3 = − − = −

2、化为三角行列式 利用行列式的性质将行列式主对角线下方的元素全化 为零，即化为上三角行列式，行列式的值为主对角线 上元素的连乘积。 4.13-1 -2 ≥6 5 3 例3计算行列式D= 12 0 3 5 2 解： 1 2 -1 0 1 2 -1 0 ←→3 -2 -6 5 3 3-4斯 2+2 D 0 -2 3 3 4 1 3 = 4-35 0 -7 7 -1 3 5 2 4 0 -1 5 4

. 3 5 2 4 1 2 1 0 2 6 5 3 4 1 3 1 − − − − 例3 计算行列式 D = 3 5 2 4 4 1 3 1 2 6 5 3 1 2 1 0 1 3 − − − − = − r r D 解: 0 1 5 4 0 7 7 1 0 2 3 3 1 2 1 0 2 1 3 1 4 1 2 4 3 − − − − − = − + − − r r r r r r 2、化为三角行列式 利用行列式的性质将行列式主对角线下方的元素全化 为零，即化为上三角行列式，行列式的值为主对角线 上元素的连乘积

12 -1 0 1 2 -1 0 h40 -1 5 4 5-720 -1 J 4 = 0 -7 7 -1 r4-2n0 0 -28 -29 0 -2 3 3 00 -7 -5 12 -1 0 1 2 -1 0 0 -1 5 4 4-43 0 一1 5 4 =一 0 0 -7 -5 0 0 -7 -5 0 0 -28 -29 0 0 0 -9 =-1×(-1)×(-7)×(-9)=63. 由于化简过程具有程序化，因此工程技术上，常用计 算机编制程序计算高阶行列式的值

= −1(−1)(−7)(−9) = 63. 0 0 0 9 0 0 7 5 0 1 5 4 1 2 1 0 4 3 4 − − − − − = − r − r 0 0 28 29 0 0 7 5 0 1 5 4 1 2 1 0 3 4 − − − − − − = − r r 由于化简过程具有程序化，因此工程技术上，常用计 算机编制程序计算高阶行列式的值。 0 2 3 3 0 7 7 1 0 1 5 4 1 2 1 0 2 4 − − − − − = r r 0 0 7 5 0 0 28 29 0 1 5 4 1 2 1 0 3 2 4 2 7 2 − − − − − − = − − r r r r

例4设多项式 1、 2 3 2 3 f(x)= 2 3 5 2 3 试求f(x)=0的根. 解方法一 1 1 2 3 4-5 1 1 2 3 2 2-x2 2 U 3-24 01-x2 0 0 f(x)= 2 3 1 5 0 1 -3 -1 2 3 19-x2 2- 0 04-x2

− = − 2 2 1 1 2 3 1 2 2 3 ( ) . 2 3 1 5 2 3 1 9 x f x x 例4 设多项式 解 方法一 − = − 2 2 1 1 2 3 1 2 2 3 ( ) 2 3 1 5 2 3 1 9 x f x x 4 3 3 1 2 1 2 r r r r r r − − − − − − − 2 2 1 1 2 3 0 1 0 0 0 1 3 1 0 0 0 4 x x 试求 f x( ) 0 = 的根

2 3 11 2 3 分3 0 -3 -1 5-(1-x252 01 -3 -1 0 0 0 00 31-x2) 1-x 0 0 0 4-x2 00 0 4-x2 =-31-x2)(4-x2). 2 3 让f(x)=0,解得：x12=1,x3,4=+2. 1 2-x2 2 3 f(x) 2 3 9-x 方法二由性质1.2.2推论知，当2-x2=1或9-x2=5 时，方程成立，即x2=±1，x3,4=+2为f(x)=0的根 由于原方程为关于x的4次多项式，因此原方程只有4个根

2 3 r r  − − − − − 2 2 1 1 2 3 0 1 3 1 0 1 0 0 0 0 0 4 x x 2 3 2 r x r − − (1 ) − − − − − − 2 2 2 1 1 2 3 0 1 3 1 0 0 3(1 ) 1 0 0 0 4 x x x = − − − 2 2 3(1 )(4 ). x x 让 f x( ) 0, = 解得：x x 1,2 3,4 =  =  1, 2. 方法二 − = 2 由性质1.2.2推论知，当 2 1 x 或 − = 2 9 5 x 由于原方程为关于x的4次多项式，因此原方程只有4个根. 时，方程成立，即 x x 1,2 3,4 =  =  1, 2 为 f x( ) 0 = 的根. 2 2 1 1 2 3 1 2 2 3 ( ) . 2 3 1 5 2 3 1 9 x f x x − = −

3、拆行拆列法 x31 1-x1-y 1-z 例5设 y01=1,求D= 4 3 z21 1 1 1 11 -x -v -z -x -y- 解： D= 4 13 4 1 3 1 3 1 1 1 1 1 11 1 31 2-3 3 0 2 y 01=-1. 11 1 z21

解: 3 1 0 1 1, 2 1 x y z 例5 设 = 求 1 1 1 4 1 3 . 1 1 1 x y z D − − − = 1 1 1 4 1 3 4 1 3 1 1 1 1 1 1 x y z D − − − = + 3、拆行拆列法 4 1 3 1 1 1 − − − x y z = 2 3 3 0 2 1 1 1 x y z r r − − 3 1 0 1 1. 2 1 x y z = − = −

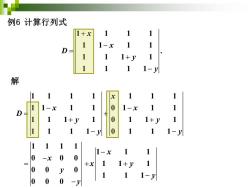
例6计算行列式 1+x 11 1-x 1 1 D 1 1 1+y 1 1 11-y 解 1 1 1 1 1 1-x 1 1-x 1 1 D 1+y 1 1+y 1 1 1 1-y 0 1 1-y 11 1 1-x 1 1 0 -x 0 0 +x 1 1+y 1 0 0 y 0 1 1 1-y 0 0 0 -列

+ − = + − 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 x x D y y 例6 计算行列式 解 − − = + + + − − 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 x x x D y y y y − = − 1 1 1 1 0 0 0 0 0 0 0 0 0 x y y − + + − 1 1 1 1 1 1 1 1 1 x x y y