《线性代数》课程教学资源（试卷习题，B）线性代数试题及答案1

题号 二 四 总分 得分 8、二次型f,5,5=2+3++25+2，是正定的，则：的取值范围 得分☐一、选择题（本题共4小题，每小题4分，满分16分。 每小题给出的四个选项中，只有一项符合题目要求) 得分☐三、计算题（本题共2小题，每题8分，满分16分） 1、设A,B为n阶方阵，满足等式4B=0,则必有() +x11 )A=0或B=0:)4+B=0;(C)4=0或=0；(D)4+=0。 11-x11 2、A和B均为n阶矩库，且(A+B=2+2AB+B,则必有（) ()A=E(⑧)B=E:(C)A=B. ()AB=B4, 3、设4为m×n矩阵，齐次方程组杠=0仅有零解的充要条件是（ ()A的列向量线性无关； (⑧)A的列向量线性相关； (C)A的行向量线性无关： ()A的行向量线性相关， 4、n阶矩阵4为奇异矩阵的充要条件是() )A的秩小于： ()4≠0： ()A的特征值都等于零：)A的特征值都不等于零： 得分☐二、填空题（本题共4小题，每题4分，满分16分） 5、若4阶矩阵A的行列式4=-5，r是A的伴随矩阵，则中一。 6、A为mxm阶矩阵，且4？-A-2E=0,则(4+2E= 10、计算n阶行列式 第1页共7页

第 1 页 共 7 页 题 号 一 二 三 四 五 总分 得 分 一、选择题（本题共 4 小题，每小题 4 分，满分 16 分。 每小题给出的四个选项中，只有一项符合题目要求） 1、设 A，B 为 n 阶方阵，满足等式 AB  0，则必有（ ） (A) A  0或B  0 ; (B) A  B  0； （C） A  0或 B  0 ; (D) A  B  0。 2、 A和B 均为n阶矩阵，且 2 2 2 (A B)  A  2AB  B ，则必有（ ） (A) A  E ； (B) B  E ； （C） A  B . (D) AB  BA。 3、设 A为m  n矩阵，齐次方程组 Ax  0仅有零解的充要条件是（ ） (A) A的列向量线性无关； (B) A的列向量线性相关； （C） A的行向量线性无关； (D) A的行向量线性相关. 4、 n阶矩阵 A为奇异矩阵的充要条件是（ ） (A) A的秩小于n； (B) A  0； (C) A的特征值都等于零； (D) A的特征值都不等于零； 二、填空题（本题共 4 小题，每题 4 分，满分 16 分） 5、若 4 阶矩阵 A的行列式 A  5， A 是 A 的伴随矩阵，则  A = 。 6、 A为n n阶矩阵，且 2 A  A 2E  0，则 1 (A 2E)    。 7、已知方程组                      4 3 1 1 2 2 3 2 1 2 1 3 2 1 x x x a a 无解，则a  。 8、二次型 2 2 2 1 2 3 1 2 3 1 2 1 3 f (x , x , x )  2x 3x tx  2x x  2x x 是正定的，则t 的取值范围 是 。 三、计算题（本题共 2 小题，每题 8 分，满分 16 分） 9、计算行列式 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 x x D y y      10、计算n阶行列式 得分 得分 得分

+3 11、若向量组a,a,a,线性相关，向量组a,a,a,线性无关。证明： D.= (1)a,能有a,a3钱性表出： (2）a,不能由a,a,a,线性表出。 12、设A是n阶矩方阵，E是n阶单位矩阵，A+E可逆，且 fA)=(E-A(E+4A)-。 证明 （1)(E+f(AE+A)=2E: (2)ff4)=A。 得分☐四、证明题（本题共2小题，每小题8分，满分16分。 写出证明过程) 第2页共7页

第 2 页 共 7 页 1 2 1 2 1 2 3 3 3 n n n n x x x x x x D x x x           四、证明题（本题共 2 小题，每小题 8 分，满分 16 分。 写出证明过程） 11、若向量组 1 2 3  , , 线性相关，向量组 2 3 4  , , 线性无关。证明： (1) 1能有 2 3  , 线性表出； (2) 4不能由 1 2 3  , , 线性表出。 12 、 设 A 是 n 阶 矩 方 阵 ， E 是 n 阶 单 位 矩 阵 ， A  E 可 逆 ， 且 1 f (A) (E A)(E A)     。 证明 （1） (E  f (A))(E  A)  2E ； （2） f ( f (A))  A。 得分

得分五、解答题（本愿共3小题，每小愿12分，满分32分。 解答应写出文字说明或演算步骤) (200 13、设A=032,求一个正交矩阵P使得P4P为对角矩阵。 023 工1+3+=0 14、已知方程组{x+2x:+m1=0与方程组x+2x+3=a-1有公共解。 +4:+a2x3=0 求a的值。 第3页共7或

第 3 页 共 7 页 五、解答题（本题共 3 小题，每小题 12 分，满分 32 分。 解答应写出文字说明或演算步骤） 13、设 2 0 0 0 3 2 0 2 3 A        ，求一个正交矩阵P 使得 1 P AP  为对角矩阵。 14、已知方程组               4 0 2 0 0 3 2 1 2 1 2 3 1 2 3 x x a x x x ax x x x 与方程组 2 1 x1  x2  x3  a  有公共解。 求a的值。 得分

1 3 4 求该方程组的通解。 15、设四元非齐次线性方程组的系数矩阵的秩为3，已知m,2,是它 的三个解向量，且 第4页共7页

第 4 页 共 7 页 15、设四元非齐次线性方程组的系数矩阵的秩为 3，已知1， 2，3是它 的三个解向量，且        5 4 3 2 1 ，         4 3 2 1  2 3 求该方程组的通解

解答和评分标准 一、选择恩 1、C: 2、Ds 3、A: 4、A. 10、解：把各列加到第一列，然后提取第一列的公因子三+3小再通 二、填空题 过行列式的变换化为上三角形行列式 5、-125: 6、: 7、-1: 8心 三、计算题 (4分) 9、解：第一行减第二行，第三行减第四行得： 12x。+3 x x 00 13x.x 11-x11 3 0 D= o 0 yy h111- 003 第二列减第一列，第四列减第三列得： (4分) 000 D= -x10 四、证明题 (4分) 00y0 101- 11、证明： 按第一行展开得 (1)、因为a:,a,a,线性无关，所以a,a线性无关。， 又aa,a,线性相关，故a能由a,a,线性表出。 (4分) ra1,马a)=3, 按第三列展开得 (2)、（反正法)若不，则a能由a,a,a,钱性表出， 不妨设a,=k,+ka,+k3· (4分) 由(1)知，g,能由1，a线性表出， 第5页共7页

第 5 页 共 7 页 解答和评分标准 一、选择题 1、C； 2、D； 3、A； 4、A。 二、填空题 5、-125; 6、 2  ； 7、-1； 8、 5 3 t  。 三、计算题 9、解：第一行减第二行，第三行减第四行得： 0 0 1 1 1 1 0 0 1 1 1 1 x x x D y y y    第二列减第一列，第四列减第三列得： 0 0 0 1 1 0 0 0 0 1 0 1 x x D y y    （4 分） 按第一行展开得 1 0 0 0 0 1 x D x y y    按第三列展开得 2 2 0 1 x D xy x y y     。 （4 分） 10、解：把各列加到第一列，然后提取第一列的公因子         n i i x 1 3 ，再通 过行列式的变换化为上三角形行列式 2 2 1 2 1 1 3 3 1 3 n n n n i i n x x x x D x x x                   （4 分） 2 1 1 0 3 0 3 0 0 3 n n i i x x x                 1 1 3 3 n n i i x            （4 分） 四、证明题 11、证明： (1)、 因为 2 3 3  ， , 线性无关，所以  2 ， 3线性无关。， 又1 ， 2 ， 3线性相关，故1 能由  2 ， 3 线性表出。 (4 分) 1 2 3 r( ， ， )  3 ， （2）、（反正法）若不，则 4能由 1 2 3  ， , 线性表出， 不妨设 4 11 2 2 3 3  k  k  k 。 由（1）知，1 能由  2 ， 3线性表出

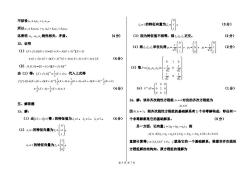
不妨设a,=4+h· 0 方=5的特征向量为5 (3分) 所以a4=k(a2+2a3)+ka:+ka3 1 这表明a,a,a线性相关，矛盾。 (4分) (3)因为特征值不相等，则5，6正交。 (2分) 12、证明 0 (4)将，5a,5单位化得n= (2分) (1)(E+f八4)E+A)=[E+(E-A(E+A)-E+A) =(E+A0+(E-A0(E+A)-(E+A)=(E+A)+(E-A)=2E (4分) 01 0 (2)f(()=[E-f(+( (5)取P=(A,PP3)= 。0 由(1)得：E+r-E+0,代入上式得 0 1 f=E-(E-4E++0=E+0-(E-AE+0E+ (100N +0-0=4 (4分) (6)P-AP=020 (1分) 005 14、解：该非齐次线性方程组A红=b对应的齐次方程组为 五、解答题 Ar=0 13、解： 因)=3，则齐次线性方程组的基础解系有1个非零解构成，即任何一 (1)由E-=0得4的特征值为2=1,2=2，=5。 (4分) 个非零解都是它的基础解系。 (5分) 0 另一方面，记向量5=2-(m:+),则 (2)名=1的特征向量为气=-， A5=A2n-乃2-3)=2An,-A72-A73=2b-b-b=0 直接计算得：=(3,45,6±0，就是它的一个基础解系。根据非齐次线性 方=2的特征向量为5 0 方程组解的结构知，原方程组的通解为 第6页共7页

第 6 页 共 7 页 不妨设1 1 2 2  3  t  t 。 所以 4 1 1 2 2 3 2 2 3 3   k (t   t  )  k   k  ， 这表明 2 3 4  ， , 线性相关，矛盾。 (4 分) 12、证明 （1） 1 (E f (A))(E A) [E (E A)(E A) ](E A)         1 (E A) (E A)(E A) (E A) (E A) (E A) 2E             （4 分） （2） 1 f ( f (A)) [E f (A)][E f (A)]     由（1）得： 1 1 [ ( )] ( ) 2 E f A E A     ，代入上式得 1 1 1 1 1 ( ( )) [ ( )( ) ] ( ) ( ) ( )( ) ( ) 2 2 2 f f A E E A E A E A E A E A E A E A              1 1 ( ) ( ) 2 2  E  A  E  A  A （4 分） 五、解答题 13、解： （1）由 E  A  0 得 A的特征值为 1  1， 2   2， 3   5。 （4 分） （2） 1  1的特征向量为 1 0 1 1         ， 2   2的特征向量为 2 1 0 0         ， 3   5的特征向量为 3 0 1 1        。 （3 分） （3）因为特征值不相等，则 1 2 3  , , 正交。 （2 分） （4）将 1 2 3  , , 单位化得 1 0 1 1 2 1 p         ， 2 1 0 0 p        ， 3 0 1 1 2 1 p        （2 分） （5）取  1 2 3  0 1 0 1 1 , , 0 2 2 1 1 0 2 2 P p p p          （6） 1 1 0 0 0 2 0 0 0 5 P AP         （1 分） 14、解：该非齐次线性方程组 Ax  b对应的齐次方程组为 Ax  0 因R(A)  3，则齐次线性方程组的基础解系有 1 个非零解构成，即任何一 个非零解都是它的基础解系。 （5 分） 另一方面，记向量 2 ( )   1  2 3 ，则 (2 ) 2 2 0 A  A 1  2 3  A1  A 2  A3  b  b  b  直接计算得  (3,4,5,6)  0 T  ， 就是它的一个基础解系。根据非齐次线性 方程组解的结构知，原方程组的通解为

(3) -1 x=k+=k 4,KER. (7分) 所以①与②的全部公共解为 0 :为任意常数. (4分) 5 2°当a=2时，有4)==3，方程组③有唯一解，此时 15、解：将①与②联立得非齐次线性方程组： (1000 ■0 0101 x,+25+a匹3 =0, ⑧ 001-1 x+4x+a2x3■0， 000 +2x2+x3=a-1. 0 若此非齐次线性方程组有解，则①与②有公共解，且⑧的解即为所求全 故方程组③的解为：1， 即①与②有唯一公共解 (4分) -1 部公共解。 对③的增广矩阵A作初等行变换得： 4分) 121a-1 001-a 1°当a=1时，有r(A)=r(=2<3,方程组③有解，即①与②有公共解，其 全部公共解即为③的通解，此时 1010 0100 00001 (0000 则方程组③为齐次线性方程组，其基础解系为 第7页共7或

第 7 页 共 7 页                 5 4 3 2 6 5 4 3 1 x k  k ，k  R。 （7 分） 15、解：将①与②联立得非齐次线性方程组:                   2 1. 4 0, 2 0, 0, 1 2 3 3 2 1 2 1 2 3 1 2 3 x x x a x x a x x x ax x x x ③ 若此非齐次线性方程组有解, 则①与②有公共解, 且③的解即为所求全 部公共解. 对③的增广矩阵 A作初等行变换得:          1 2 1 1 1 4 0 1 2 0 1 1 1 0 2 a a a A            0 0 1 1 0 0 ( 2)( 1) 0 0 1 1 0 1 1 1 0 a a a a a . （4 分） 1°当a 1时，有r(A)  r(A)  2  3，方程组③有解, 即①与②有公共解, 其 全部公共解即为③的通解，此时        0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 A ， 则方程组③为齐次线性方程组，其基础解系为:        1 0 1 , 所以①与②的全部公共解为        1 0 1 k ，k 为任意常数. （4 分） 2° 当a  2时，有r(A)  r(A)  3，方程组③有唯一解, 此时         0 0 0 0 0 0 1 1 0 1 0 1 1 0 0 0 A ， 故方程组③的解为: 0 1 1        , 即①与②有唯一公共解 0 1 1 x         . （4 分）