《线性代数》课程教学课件（PPT讲稿，B）第五章 相似矩阵与二次型_5-1 第一节 向量的内积及正交向量组

第五章相似矩阵与二次型 第一节 向量的阳积及正交向量组

第五章 相似矩阵与二次型 第一节 向量的内积及正交向量组

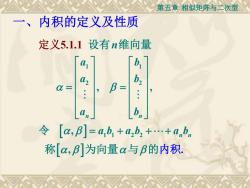
第五章相似矩阵与二次型 一、 内积的定义及性质 定义5.1.1设有n维向量 42 b2 = B= .: b 令[a,B]=ab1+ub2+.+anbn 称[a,B]为向量x与B的内积

第五章 相似矩阵与二次型     1 1 2 2 1 1 2 2 , , , , 5.1.1 . n n n n n a b a b a b a b a b a b                     = =             = + + + 设有 维向量 令 称 为向量 与 定 的内积 义 一、内积的定义及性质

第五章相似矩阵与二次型 内积的运算性质 a,B]=aa++abn (其中a,B,y为n维向量，为实数)： [aB]=[B,a]; (2)[a,B]=[a,B]: (3)[a+B,r]=[a,r]+[B,y]: (4)[a,a]≥0，且当a≠0时有a,a>0

第五章 相似矩阵与二次型 内积的运算性质 (其中    , , , : 为n维向量 为实数) (1) , , ;      =   (2) , , ;       =   (3) , , , ;        + = +      (4) [ , ] 0, 0 [ , ] 0.         且当 时有   1 1 2 2 , n n   = + + + a b a b a b

第五章相似矩阵与二次型 二、向量的长度及性质 定义5.12非负数√[a,a=√++.+称为向量 a的长度（或范数），记作a 向量的长度具有下述性质： 1.非负性当a≠0时，a>0;当a=0时，a=0; 2.齐次性2a=2‖la; 3.三角不等式la+l≤a+Bl:

第五章 相似矩阵与二次型 定义5.1.2   2 2 2 1 2 , . n   a a a   非负数 = + + + 称 长度(或范数 量 的 ) 为向 ，记作 向量的长度具有下述性质： 1. 0 , 0; 0 , 0; 非负性 当      = = 时 当 时 2. ; 齐次性    = 3. . 三角不等式     +  + 二、向量的长度及性质

第五章相似矩阵与二次型 若ag=1,则称a为单位向量 如果a≠0，由长度的概念得 就是一个单位向量， 用非零数 乘以向量得到一个与a同方向的 单位向量，通常称为把向量a单位化. 当la≠0，Bl≠0时，B=arccos [a,] aB 称为n维向量a与B的夹角

第五章 相似矩阵与二次型 若   = 1, . 则称 为单位向量 1   0, .  如果  由长度的概念得 就是一个单位向量 1 .     用非零数 乘以向量 得到一个与 同方向的 单位向量，通常称为把向量 单位化  ,  0, 0 , arccos n .          当   = 时 称为 维向量 与 的夹角

第五章相似矩阵与二次型 三、正交向量组的概念及求法 当[，B]=0时，称向量a与正交 定义5.1.3一组两两正交的非零向量称为正交向量组. 若正交向量组中每个向量都是单位向量，则称该向量组 为标准正交向量组

第五章 相似矩阵与二次型 定义5.1.3 一组两两正交的非零向量称为正交向量组． 若正交向量组中每个向量都是单位向量,则称该向量组 为标准正交向量组. 三、正交向量组的概念及求法 当[ , ] 0     = 时，称向量 与 正交

第五章相似矩阵与二次型 定理5.1.1 正交向量组是线性无关向量组 证明 设有a1,a2,.am是正交向量组， ka1+k2a2+.+knam=0 用4，与等式两边做内积，得 kla,a]=0i=1,2,.,m 由c,≠0，有a,a,>0,从而得 k=0i=1,2,.,m. 故c,a2,.,an线性无关

第五章 相似矩阵与二次型 0, [ , ] 0, 由   i i i   有 从而得 0 1,2, , . i k i m = = 1 2 , , , . 故   m 线性无关 [ , ] 0 1,2, , i i i k i m   = = 定理5.1.1 正交向量组是线性无关向量组. 证明 1 1 2 2 0 m m k k k    + + + = , i 用a 与等式两边做内积 得 1 2 , , , 设有   m 是正交向量组

第五章相似矩阵与二次型 设c,a2,.,a是r维向量空间V的一个基， 若%1,2，两两正交， 则称a,2,.,是向量空间的一个正交基， 由单位向量组成的正交基称为标准正交基 (或正交规范基)

第五章 相似矩阵与二次型 1 2 1 2 1 2 , , , , , , , , , ( ). r r r r V V          设 是 维向量空间 的一个基， 若 两两正交， 则称 是向量空间 的一个 ， 由单位向量组成的正交基 正交基 标准正交基 或正交规范基 称为

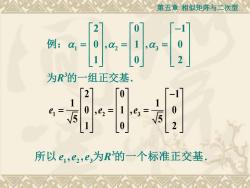
第五章相似矩阵与二次型 2 0 例：a1=0, b4,= 10 为R的 组正交基 [21 0) -1 1 1 e1= 0,e2= 1 ,e3= 5 0 1 0 2 所以e,e2,e,为R3的一个标准正交基

第五章 相似矩阵与二次型 1 2 3 2 0 1 1 1 0 , 1 , 0 5 5 1 0 2 e e e       −       = = =                   3 1 2 3 所以 e e e R , , . 为 的一个标准正交基 1 2 3 3 2 0 1 0 , 1 , 0 1 0 2 R .          −       = = =                   例： 为 的一组正交基

第五章相似矩阵与二次型 在向量空间中，如何由个线性无关的向量来找r个 两两正交的向量呢？ 若%1,2，.，C,为线性无关组， (1)正交化 取B=1 n B-&,- 8g别 [P2,C3] [B,B1 [B2,B2]

第五章 相似矩阵与二次型 在向量空间V中,如何由r个线性无关的向量来找r个 两两正交的向量呢? （1）正交化 取  1 1 = 1 2 2 2 1 1 1 , , ,            = −     1 2 , , , , 若  r 为线性无关组 1 3 2 3 3 3 1 2 1 1 2 2 [ , ] [ , ] [ , ] [ , ]             = − −