《线性代数》课程教学课件（PPT讲稿，B）第四章 线性方程组_4-1 线性方程组解的判别

线性代数 山东理工大学

线性代数 山东理工大学

第4章线性方程组 。内容提要 §4.1线性方程组解的判别 §4.2齐次线性方程组 §4.3非齐次线性方程组

第4章 线性方程组 ◼ 内容提要 §4.1 线性方程组解的判别 §4.2 齐次线性方程组 §4.3 非齐次线性方程组

第4章线性方程组 §4.1线性方程组的判别

§4.1 线性方程组的判别 第4章 线性方程组

线性方程组 设n元线性方程组为 的代数形式 21 + L b2 (1) M M M M M M M M 十 L 12 L 021 022 则称矩阵A= 为方程组()的系数矩阵 M M M L

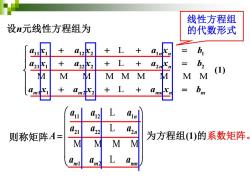
设n元线性方程组为 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L 则称矩阵 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a     =         L L M M M M L 为方程组(1)的系数矩阵。 线性方程组 的代数形式

022+L = b 未知元列向量 021水1+ × = (1) M MM MMM M M amiX1 am2x2+L amnXn 右端项列向量 M b= b M 则线性方程组等价的矩阵形线性方程组矩阵形式 Ax=b

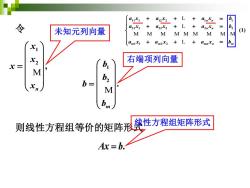
令 1 2 , n x x x x     =         M 则线性方程组等价的矩阵形式 Ax b = . 1 2 . m b b b b     =         M 未知元列向量 右端项列向量 线性方程组矩阵形式 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L

X b 对于 22 X + (1) M M M M M m2 L + mn 令 右端项列向量 12 21 b2 01= M ,02= M L,a= M b= M bm 线性方程组向量形式 则线性方程组等价的向量形式或 X1必1+x22+L+Xn0n=b

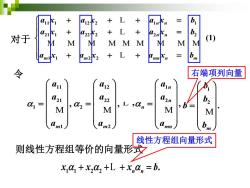
11 21 1 1 , m a a a      =         M 则线性方程组等价的向量形式 1 1 2 2 . n n x x x b    + + + = L 1 2 . m b b b b     =         M 右端项列向量 线性方程组向量形式 对于 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L 令 12 22 2 2 , m a a a      =         M L , 1 2 , n n n mn a a a      =         M

Xi + x2 2x3 1 2x1 一 X2 2x3 4, 如线性方程组 2x2 3, 4x1 + 2+ 4x3 2. 1 1 2 1 2 -1 2 4 A= 1 -2 ,X= ,b= 0 3 4 1 2 容易验证x1=-1,x2=-2,x3=2是方程组的解。 -1 解向量 同样x= -2 是方程组等价的矩阵形式Ax=b的解（向 2 量)

如线性方程组 1 2 3 1 2 3 1 2 1 2 3 2 1, 2 2 4, 2 3, 4 4 2. x x x x x x x x x x x  ++=   − + =  − =   ++=  1 1 2 2 1 2 , 1 2 0 4 1 4 A     − =     −     1 2 3 , x x x x     =       1 4 . 3 2 b     =         容易验证 x x x 1 2 3 = − = − = 1, 2, 2 是方程组的解。 同样 是方程组等价的矩阵形式 的解(向 量)。 1 2 2 x   −   = −      Ax b = 解向量

01X1 b L21X1 对于 (1) M M M M M M MM M 0m1x1+ 0m2X2 +L+ amnn= bm 1 L12 L n b 称矩阵A=(A,b)= L21 L22 L 2n M M M M M Ami Am2 L Amn bm 为方程组(1)的增广矩阵

称矩阵 11 12 1 1 21 22 2 2 1 2 ( , ) n n m m mn m a a a b a a a b A A b a a a b     = =         L L M M M M M L 为方程组(1)的增广矩阵。 对于 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =     + + + = L L M M M M M M M M M L

当b=0(i=1,2,L,m)时，齐次线性方程组 411X1+ 0 021x1 十 022X2 a2nXn 2) M M MMMM M MM amix1 am2x2 +L 0 称为非齐次线性方程组(1)对应的齐次线性方程 组

称为非齐次线性方程组（1）对应的齐次线性方程 组。 当 0 ( 1,2, , ) i b i m = = L 时,齐次线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 (2) 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x  + + + =   + + + =     + + + = L L M M M M M M M M M L

定义：线性方程组的初等变换（加减消元法） (1) 互换两个方程的位置； (2)用一非零的数乘某一方程； (3)把一个方程的倍数加到另一个方程。 可以证明一个线性方程组经过若干次初等变换， 所得到的新的线性方程组与原方程组同解。 对一个方程组进行初等变换，实际上就是对它的增广矩 阵做初等行变换， 初等行变换 A=(A,b)~

定义：线性方程组的初等变换（加减消元法） （2） 用一非零的数乘某一方程; （3） 把一个方程的倍数加到另一个方程. （1） 互换两个方程的位置; 可以证明一个线性方程组经过若干次初等变换， 所得到的新的线性方程组与原方程组同解。 对一个方程组进行初等变换，实际上就是对它的增广矩 阵做初等行变换. A A b = ( , )~ 初等行变换