《线性代数》课程教学课件（PPT讲稿，B）第三章 矩阵的运算_3-2 逆矩阵

线性代数 山东理工大学

线性代数 山东理工大学

第3章矩阵的运算 §3.2 逆矩阵 逆矩阵的定义、唯一性 ·矩阵可逆的条件 ·可逆矩阵的运算性质

§3.2 逆矩阵 第3章 矩阵的运算 ● 逆矩阵的定义、唯一性 ● 矩阵可逆的条件 ● 可逆矩阵的运算性质

1.逆矩阵的定义、唯一性 概念的引入：在数的运算中，当数α≠0时，有 aa"=aa=1, 其中a-为a的倒数，（或称a的逆）； 在矩阵的运算中，单位阵E相当于数的乘法运算中的1， 那么，对于矩阵A,如果存在一个矩阵A1, 使得AA=AA=E, 则矩阵A一称为A的可逆矩阵或逆阵

1.逆矩阵的定义、唯一性 1, 1 1 = = − − aa a a 则矩阵 称为 A 的可逆矩阵或逆阵. −1 A 概念的引入: 在数的运算中，当数 a  0 时，有 a a 1 1 = − 其中 为 a 的倒数，（或称 a 的逆）； 在矩阵的运算中，单位阵 E 相当于数的乘法运算中的1， 那么，对于矩阵 A ， −1 如果存在一个矩阵 A , , 1 1 AA = A A = E − − 使得

定义 设A为n阶方阵，若存在n阶方阵B,使得 3.2.1: AB=BA=E,则称矩阵A是可逆的，方阵B 称为A的逆矩阵，记作A1=B。 侧：变4=少8=（好1 QAB=BA=E,∴.B是A的一个逆矩阵 唯一性：若A是可逆矩阵，则A的逆矩阵是唯一的. 证明：设B、C都是A的逆矩阵，则 AB=BA=E,AC=CA=E, 从而B=EB=(CA)B=C(AB)=CE=CD 矩阵乘法的结合律

定义 3.2.1： 1 AB B A n n B A B A A A E B 设 阶方阵，若存在 阶方阵 ，使得 ，则称矩阵 是可逆的，方阵 称为 的逆矩阵，记作 。 为 − = = = 例: 设 , 1 2 1 2 1 2 1 2 , 1 1 1 1       −  =      − A = B Q AB BA E = = , B是A的一个逆矩阵. 唯一性：若A是可逆矩阵，则A的逆矩阵是唯一的. 证明： 设B C A 、 都是 的逆矩阵，则 AB BA E AC CA E = = = = ， ， 从而B EB = = ( ) CA B = C AB ( ) = = CE C。 矩阵乘法的结合律

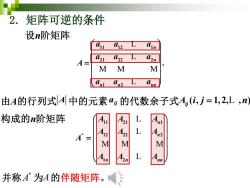
2.矩阵可逆的条件 设n阶矩阵 012 021 22 A= M M M 由A的行列式A中的元素a的代数余子式A,(i,j=1,2,L,n 构成的n阶矩阵 n L A" M M M 1n nn 并称A为A的伴随矩阵

2. 矩阵可逆的条件 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A       =       L L M M M L 11 12 1 21 22 2 1 2 . n n n n nn a a a a a a A a a a       =       L L M M M L 设n阶矩阵 ij 由A的行列式 A 中的元素 a 的代数余子式 构成的n阶矩阵 ( , 1,2, , ) A i j n ij = L A * 并称A 为 的伴随矩阵

对于A中元素a,代数余子式A;,由于 an+:+l+a.=4=方 0,i≠j A,i=j, au d+aj 则 L (4 21022 L AA= An MM M M M M n L

1 1 2 2 1 1 2 2 , , 0, . , , 0, . i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    L L 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =             L L L L M M M M M M L L ij 对于 A 中元素 a 代数余子式 Aij ，由于 则 0 0 0 = 0 0 0 A A A             L L M M M L A

对于A中元素a,代数余子式A,由于 h+a4l+a4=i=方 0,i≠j: l,i=j, a4,+a4,+l+04,={0,it. 则 Au L AA" A L MM M M M M Lam八 k。L

1 1 2 2 1 1 2 2 , , 0, . , , 0, . i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    L L 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =             L L L L M M M M M M L L ij 对于 A 中元素 a 代数余子式 Aij ，由于 则 0 0 0 = 0 0 0 A A A             L L M M M L A 0 L

对于A中元素a,代数余子式A;,由于 an+:+l+a.=4=方 0,i≠j ,i=j, au d+aj 则 A L AA" L2122 MM M M M 。 An2 L A

1 1 2 2 1 1 2 2 , , 0, . , , 0, . i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    L L 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =             L L L L M M M M M M L L ij 对于 A 中元素 a 代数余子式 Aij ，由于 则 0 0 0 = 0 0 0 A A A             L L M M M L A 0 L 0

对于A中元素a,代数余子式A,由于 h+a4l+a4=i=方 0,i≠j. l,i=j, a4+aA+1.+aA=0,i*i. 则 a1112L4n） A2 L AA" 2122 A L 0 MM M M M M L L

1 1 2 2 1 1 2 2 , , 0, . , , 0, . i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    L L 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =             L L L L M M M M M M L L ij 对于 A 中元素 a 代数余子式 Aij ，由于 则 0 0 0 = 0 0 0 A A A             L L M M M L A 0 0 0 L

对于A中元素a,代数余子式A;,由于 anAn arAn+L amAm= l,i=j, 0,i≠j ,i=j, a4+a4,+l+aeAg=0,i≠i小 则 L 140L0 AA'= L 0 L M M M M M M 人

1 1 2 2 1 1 2 2 , , 0, . , , 0, . i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j  = + + + =     = + + + =    L L 11 12 1 11 21 1 * 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a A A A a a a A A A AA a a a A A A             =             L L L L M M M M M M L L ij 对于 A 中元素 a 代数余子式 Aij ，由于 则 0 0 0 = 0 0 0 A A A             L L M M M L A A 0 0 0 L L