《线性代数》课程教学课件（PPT讲稿，B）第五章 相似矩阵与二次型_5-5 二次型及其标准型

线性代数 山东理工大学

线性代数 山东理工大学

第5章相似矩阵和二次型 §5.5二次型及其标准型 ·二次型及其矩阵表示 ●化二次型为标准形

§5.5 二次型及其标准型 ● 二次型及其矩阵表示 ● 化二次型为标准形 第5章 相似矩阵和二次型

二次型的理论起源于化二次曲线、二次曲面的方程 为标准形的问题。 方程的左边既有平 方项，又有交叉项 如二次曲线：x2+xy+y2=1. 选择适当的角度0作旋转变换： 2 2 x=x'cos0-y'sine 0- 2 y=x'sin0-y'cos0→ y= 正交矩阵 令：P= 2 2 2

二次型的理论起源于化二次曲线、二次曲面的方程 为标准形的问题。 如二次曲线： 2 2 x xy y + + = 1. 选择适当的角度  作旋转变换： cos sin sin cos x x y y x y      = −    = −    4   =  2 2 2 2 2 2 2 2 x x y y x y  = −       = −    令： ，则 2 2 2 2 2 2 2 2 P     − =         x x P y y     =         正交矩阵 方程的左边既有平 方项，又有交叉项

称矩阵P为从x',y'到x,y的线性变换矩阵。 将此变换代入原二次曲线得： (Ξj〔源+学j 方程的左边 →层+ 只有平方项 问题：如何把一般的二次齐次多 8=45 0 项式经过可逆线性变换化成只含 -0.5 平方和的形式。 二次曲面：y+z+水=0. -15

2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 x y x y x y x y                       − + − + + + =         称矩阵P为从 x y   , 到 x y, 的线性变换矩阵。 问题：如何把一般的二次齐次多 项式经过可逆线性变换化成只含 平方和的形式。 3 1 2 2 1. 2 2 x y   + = 方程的左边 只有平方项 将此变换代入原二次曲线得： 二次曲面： xy yz zx + + = 0

二次型及其矩阵表示 1.二次型、二次型的矩阵、二次型的秩 定义1：含有n个变量x1,x2,L,xn的二次齐次多项式 f(x,x2,L,x) =a1x+2a2-xx2+2a13x53+L+21nx2 +a2x号+2a232-63+L+2nx2。 +L +0-2+2aw。 称为二次型。（1)

一 . 二次型及其矩阵表示 1. 二次型、二次型的矩阵、二次型的秩 称为二次型。（1） 1 2 2 11 1 12 1 2 13 1 3 1 1 2 22 2 23 2 3 2 2 2 1, 1 1 1, 1 ( , , , ) 2 2 2 2 2 2 n n n n n n n n n n n n f x x x a x a x x a x x a x x a x a x x a x x a x a x x − − − − − = + + + + + + + + + + + L L L L 2 nn n + a x 定义1：含有 n 个变量 x x x 1 2 , , , L n 的二次齐次多项式

实二次型：，为实数。（我们仅讨论实二次型） 复二次型：，为复数。 例如：f(x,y)=x2+4y+5y2 f(x,y,z)=2x2+y2+xz+yz 都是二次型。 f(x1,x2,3)七4)=x1x2+x2x3+x2x4 f(x,y)=x2+y2+5 f(x,y)=2x2-y2+2x }不是次

实二次型： aij 为实数。（我们仅讨论实二次型） 复二次型： aij 为复数。 例如： 2 2 f x y x xy y ( , ) 4 5 = + + 2 2 f x y z x y xz yz ( , , ) 2 = + + + 1 2 3 4 1 2 2 3 2 4 f x x x x x x x x x x ( , , , ) = + +      都是二次型。 2 2 f x y x y ( , ) 5 = + + 2 2 f x y x y x ( , ) 2 2 = − +    不是二次型

只含有平方项的二次型f=ky+k2y经+.+kn 称为二次型的标准形。 例如：f(x1,2,x)=2x+4x号+5x号-4xK3 f(x1,2,3)=2+Xx3+x23 都为二次型； f(1,x2,K3)=x+4x3+4x 为二次型的标准形

只含有平方项的二次型 2 2 2 2 2 1 1 n n f = k y + k y ++ k y 称为二次型的标准形。 例如： ( ) 1 3 2 3 2 2 2 1 2 3 1 f x , x , x = 2x + 4x + 5x − 4x x 都为二次型； ( ) 2 3 2 2 2 1 2 3 1 f x , x , x = x + 4x + 4x 为二次型的标准形。 ( ) 1 2 3 1 2 1 3 2 3 f x , x , x = x x + x x + x x

取0=0 则2ag火j=xx;+anX:Xj 则(1)式可以表示为 f=auxi+anx:x2+L+aunxxn +21X2X1+22x号+L+2m2n +① 二次型用和号表示 +5+a5t+a=a =X,(a111+012X2+L+41mn) +X2(a21X1+22X2+L+42mXn) +L +x(amx1+an2x2+L amnx)

2 2 11 12 2 1 1 2 1 21 1 22 2 1 1 2 2 2 2 1 2 n n n n n n nn n n n f a a x a x a x a x x a x x x x a a a x x x x x = + + + x + + + + + + + + + L L L L ij ji 取 a a = 2 ij i j ij i j ji i j 则 a x x a x x a x x = + 则（1）式可以表示为 1 11 1 12 2 1 ( ) n n = + + + x a x a x x L a 2 21 1 22 2 2 ( ) n n + + + + x a x a x x L a +L 1 1 2 2 ( ) n n n nn n + + + + x a x a x L a x , 1 n ij i j i j a x x = =  二次型用和号表示

411七1+012x2+L+41nXn az1x1+a22x2+L+aznx =(x1,x2,L,xn) M amx1+an2x2+L+amnxn 12 L 21 l22 L =(X13X2,L,Xn) Q2n 七 M M L x

11 1 12 2 1 21 1 22 2 2 1 2 1 1 2 2 ( , , , ) n n n n n n n nn n a x a x a x a x a x a x x x x a x a x a x   + + +   + + +   =     + + +   L L L M L 11 12 1 1 21 22 2 2 1 2 1 2 ( , , , ) n n n n n nn n a a a x a a a x x x x a a a x          =          L L L M M L

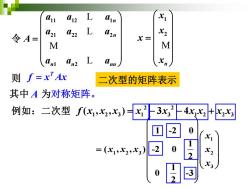
11 L12 L Qin X1 令A= 21 42 L Q2n X= M M An An2 L 则f=x'Ax 二次型的矩阵表示 其中A为对称矩阵。 例如：二次型f(x,七，)x3x,2 4 回-2 0 =(x1,X2,x3) 2

1 2 n x x x x       =       M 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a     =         L L M L 令 T 则 f x Ax = 其中 A 为对称矩阵。 二次型的矩阵表示 1 1 2 3 2 3 1 -2 0 1 ( , , ) -2 0 2 1 0 -3 2 x x x x x x         =              2 2 1 2 3 1 3 1 2 2 3 例如：二次型 ( , , ) 3 4 f x x x x x x x x x = − − +