《线性代数》课程教学课件（PPT讲稿，B）第二章 矩阵与向量_2-2 向量及其线性运算

线性代数 山东理工大学

线性代数 山东理工大学

第2章矩阵与向量 §2.2 向量及其线性运算 ·向量的概念 ·向量的运算和性质 ·向量空间

§2.2 向量及其线性运算 第2章 矩阵与向量 ● 向量的概念 ● 向量的运算和性质 ● 向量空间

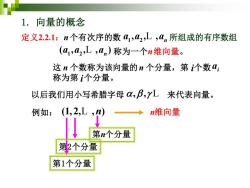
1.向量的概念 定义2.2.1：n个有次序的数41,42，L,0n所组成的有序数组 (41,a2,L,0n)称为一个n维向量。 这n个数称为该向量的n个分量，第个数4； 称为第个分量。 以后我们用小写希腊字母α，B,YL来代表向量。 例如： →n维向量 第n个分量 第2个分量 第1个分量

1. 向量的概念 定义2.2.1：n 个有次序的数 1 2 , , , n a a a L 所组成的有序数组 ( , , , ) 1 2 L n a a a 称为一个n 维向量。 这 n 个数称为该向量的n 个分量，第 个数 称为第 个分量。 i i i a 以后我们用小写希腊字母    , , L 来代表向量。 例如： (1,2, , ) L n n维向量 第1个分量 第n个分量 第2个分量

向量通常写成一行：a=(a,42,L,4n)称为行向量。 a, 它们的区别 有时也写成一列：a= 称为列向量。 M 只是写法上 的不同。 分量全为零的向量(0,0，L,0)称为零向量。记作：O

向量通常写成一行： 1 2 ( , , , ) n  = a a a L 有时也写成一列： 1 2 n a a a     =          M 称为行向量。 称为列向量。 它们的区别 只是写法上 的不同。 分量全为零的向量 (0,0, ,0) L 称为零向量。 记作：O

如线性方程组(2.1)中： (2.1) 2） 未知量x,前的系数对应着一个3维列向量：，= 未知量x,前的系数对应着一个3维列向量：a=(-11)', 未知量x,前的系数对应着一个3维列向量：a,=(224)', 右端常数项对应着一个3维列向量：b=(412)', 线性方程组(21)的解为：七1=-2，x2=-1,x3=2. 这个解也对应着一个3维解向量：x=（-2-12)/

如线性方程组(2.1) 中 :  1 2 3 1 2 3 1 2 3 2 - 2 = 4, + 2 1, 4 + 4 2. x x + x x x + x = x x + x = (2.1) 1 未 知 量x 前 的 系 数对应着 一个 3 维列 向 量： 1 2 = 14            2 未知量x 前 的 系 数对应着 一个 3 维列 向 量： ( ) 2 = -1 1 1 , T  3 未 知 量x 前 的 系 数对应着 一个 3 维列 向 量： ( ) 3 = 2 2 4 , T  右端 常 数 项 对 应 着 一 个 3 维 列 向 量： = 4 1 2 , ( )T b 1 2 3 线 性方程组(2.1) 2, 1, 2. 的解为：x x x = − = − = 3 2 1 2 . ( )T 这个解也对应着 一个 维解 向 量：x = − −

2.向量的运算和性质 向量相等：如果n维向量a=(a1,42,L,4n) B=(b,B2,L ,b) 的对应分量都相等，即4=b(i=1,2,L,n) 就称这两个向量相等，记为α=B 向量加法：向量Y=(a1+b1,42+b2,L,0n+bn) 称为向量x=(a1,42,L,4n)B=(b1,b2,L,bn） 的和，记为y=a+B 负向量：向量&=(-4，一4，L,一0n)称为向量a的负向量， 记作：一a. 向量减法：a-B=a+(-B)

2. 向量的运算和性质 向量相等：如果n 维向量 1 2 ( , , , ) n  = a a a L 1 2 ( , , , ) n  = b b b L 的对应分量都相等，即 ( 1,2, , ) i i a b i n = = L 就称这两个向量相等，记为   = 向量加法：向量  = + + + (a b a b a b 1 1 2 2 , , , L n n ) 称为向量  = (a a a 1 2 , , , L n )  = (b b b 1 2 , , , L n ) 的和，记为    = + 负向量：向量  = − − − ( a a a 1 2 , , , L n ) 称为向量  的负向量， 向量减法：    − = + −( ) 记作：−

数乘向量：设k为某一个常数，则向量(ka1,k2L,kan) 称为向量a=(41,42,L,an) 与数k的数量乘积。记为ka 满足运算律： (1)a+B=B+a (S)1·a&=a (2)(a+B)+y=(a+B)+y(6)k(la)=(kI)a 3)a+0=a (7(k+D)a=ka+la (4)a+（-a)=0 (8)k(a+B)=ka+kB 在数学上，满足这八条规律的运算称为线性运算

数乘向量：设k为某一个常数，则向量 (ka ka ka 1 2 , , , L n ) 称为向量  = (a a a 1 2 , , , L n ) 与数k的数量乘积。记为 k (4) ( ) 0 (3) 0 (2)( ) ( ) (1) + − = + = + + = + + + = +               ( ) (  )          k k k k l k l k l kl + = + + = + =  = (8) (7) (6) ( ) ( ) (5)1 满足运算律： 在数学上，满足这八条规律的运算称为线性运算

注：(1)对任意的向量，存在唯一的零向量0， 使得a+0= (2) 对任意的向量，存在唯一的负向量-a, 使得a+（-0)=0 (30a=0;(-1)a=-a;20=0. (4)如果2a=0,则入=0或a=0 例1设向量a=(1,1,0),B=(0,1,1),y=(3,4,0),求a-B及3a+2B-Y. 解： 0 3 70 3a+2B-y=31 +2 1 =(012) 0 0

注：（1）对任意的向量 , 存在唯一的零向量 o, 使得   + = o （2）对任意的向量 , 存在唯一的负向量 −, 使得   + − = ( ) o （4）如果  = 0, 则   = = 0或 0 （3） 0 ; ( 1) ; .     = − = − = 0 0 0 解： T T 1 0 1 1 0 1           − = − =             ( ) T 1 0 1 0 1 , 1     = −       − 1 0 3 3 2 3 1 2 1 4 0 1 0 T T T                + − = + −                   ( ) T 0 1 0 1 2 . 2     = =       例1 设向量    = = = (1,1,0), (0,1,1), (3,4,0) (1,1,0), (0,1,1), (3,4,0) ,求   − 及 3 2 .    + −

3.向量空间 定义：设V为n维向量的组成的集合，如果集合V 非空，集合V对于加法及数乘两种运算封闭， 那么就称集合V为向量空间. 说明：集合V对于加法及数乘两种运算封闭指 V&∈V,B∈V,有a+B∈V; Va∈V,Hk∈R,有ka∈V. 例2：3维向量的全体R3是一个向量空间。 n维向量的全体R”,也是一个向量空间

3. 向量空间 说明:        V k R k V , , . 有    +      V V V , , ; 有 定义： 设 V 为 维向量的组成的集合，如果集合 非空，集合 对于加法及数乘两种运算封闭， 那么就称集合 为向量空间． n V V V 集合 V 对于加法及数乘两种运算封闭指 例2：3维向量的全体 是一个向量空间。 3 R n维向量的全体 R n ，也是一个向量空间

例3：判别下列集合是否能够构成向量空间. (y={x=(0,Lx'xL,x,∈R (2)V,=x=(1xL.,x)k:L,ER 解：(a=(0,a2,L,an)',B=(0,b,L,b)'e 有a+B=(0,a2+b2,L,4n+bn）'∈Y V∈R,有a=(0,a,L,an)'∈V. 所以，V是向量空间。 (2)V,不是向量空间。 因为若a=(1,a,L,an)'∈2， 则2a=(2,2a2,L,2an)'eV:

例3: 判别下列集合是否能够构成向量空间.  ( )   ( )  1 2 2 2 2 2 (1) 0, , , , , (2) 1, , , , , T n n T n n V x x x x x R V x x x x x R = =  = =  L L L L 解： (1) 0, , , , 0, , , ( 2 2 1 ) ( ) T T n n  = =    a a b b V L L (0, , , 2 2 1 ) T n n 有  + = + +  a b a b V L , 0, , , . ( 2 1 ) T   =      R a a V 有 L n 所以， V1 是向量空间。 (2) V2 不是向量空间。 2 2,2 , ,2 . ( 2 2 ) T n 则  =  a a V L (1, , , , 2 2 ) T n 因为若 =  a a V L