《线性代数》课程教学课件（讲稿，B）第三章 矩阵的运算_3.1 矩阵的运算_3.1 矩阵的运算（二）_3.1 矩阵的运算（二）

线性代数第三章 第三章矩阵的运算 §3.1矩阵的运算 S3.2逆矩阵 S3.3初等矩阵 S3.4分块矩阵 上页 下页 儿返回 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 第三章 矩阵的运算 §3.1 矩阵的运算 §3.2 逆矩阵 §3.3 初等矩阵 §3.4 分块矩阵 上页 下页 返回

线性代数第三章 S3.1.2矩阵的运算（二） 四、矩阵转置 五、n阶距阵的行列式 六、共轭矩阵 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 §3.1.2 矩阵的运算(二) 四、矩阵转置 五、n阶距阵的行列式 六、共轭矩阵

线性代数第三章 四、矩阵转置 定义3.1.4把矩阵A的行换成同序数的列得到一个 矩阵，叫做A的转置矩阵，记作A线A. 5ù 1 23 4ù 如A= 6 88 则A= 67 7ú 4 8a 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 四、矩阵转置

线性代数第三章 转置矩阵的运算律： 1.（A9e=; 2.(A+B)=Ac+Be 3.(I A)=I Ad 任一方阵都可以 分解成对称阵与 4.(AB)=BeAc 反对称阵的和 A=4+A+4-4 2 版权所有：山东理工大学理学腕

线性代数 第三章 版权所有：山东理工大学理学院 转置矩阵的运算律： 任一方阵都可以 分解成对称阵与 反对称阵的和

线性代数第三章 例9：已知 7 a2 0 A= -1 -1 B= 2 3 20 4 3 求(4B)了. 82 01 解法1： ael 7 议2 0 QAB 当 4 t= 14 -36 = 1 2 3 3 2 2 13 0 ÷ 1 7 10 ae0 176 (ay 13- 8-3 10哈 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 例9: 已知 解法1：

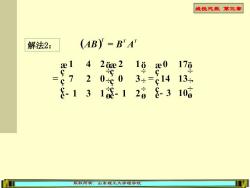
线性代数第三章 解法2： (AB)=BA" 42ae216 ae0 176 03=1413 2 8-1318-12a 8-310g 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 解法2：

线性代数第三章 例10设X=(x1,x2,L,xn)7,满足X7X=1, 且H=E-2XXT,证明H是对称阵，且HHT=E. 证H=(E-2XX)T=E-2(XX) =E-2XX'=H \H为对称阵， HHT=H2=(E-2XXT)2 =E-4(XX)+4(XX")(XXT) =E-4XXT+4X(XTX)XT =E-4XXT+4XXT=E 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 证 证明 H 是对称阵 , 例10

线性代数第三章 对称阵：设A为阶方阵，如果满足A=A',即 aa=a:(i,j=1,2,L,n) 那末称为对称阵. 义610 例如A= 为对称阵. 说明： 对称阵的元素以主对角线为对称轴对应相等】 如果AT=·A则矩阵A称为反对称的. A是对称矩阵 A=A A是反对称矩阵 0 A"=-A 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 说明： 对称阵的元素以主对角线为对称轴对应相等. 设 为 阶方阵，如果满足 ，即 那末 称为对称阵. 对称阵:

线性代数第三章 例11：对于任意的阶矩阵A证明： ()A+A'是对称矩阵，A-A是反对称矩阵. (2) A可表示为对称矩阵和反对称矩阵之和. =4+44 (A-4)=4-(4) =A"-A =-(A-A) 注：对称矩阵的乘积不一定是对称矩阵 (A+A)=A+(A) a 116 2 16 =4T+A 例 8 0 081 2 1÷= 81 1 1 =A+4 0 0 1081 13 1130 8 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 例11： 注：对称矩阵的乘积不一定是对称矩阵

线性代数第三章 五、n阶矩阵的行列式 定义3.1.5由n阶方阵A的元素所构成的行列式（各元素 位置不变称为距阵A的行列式，记为 A或detA. 例 12 ú 对角矩阵 的行列式为 e 0 e 版权所有：山东理工大学理学院

线性代数 第三章 版权所有：山东理工大学理学院 例 定义3.1.5 由n阶方阵A 的元素所构成的行列式(各元素 位置不变)称为距阵A 的行列式, 记为 五、n阶矩阵的行列式