《线性代数》课程教学课件（讲稿，B）第四章 线性方程组_4.2 齐次线性方程组_4.2 齐次线性方程组

线性代数第四章 S4.2齐次线性方程组 一、齐次线性方程组的性质 二、基础解系及其求法 三、小结 上页 下页 返回 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 三、小结 二、基础解系及其求法 一、齐次线性方程组的性质 §4.2 齐次线性方程组 上页 下页 返回

线性代数第四章 一、齐次线性方程组解的性质 设有齐次线性方程组 i41X1+412X2+L+41mXn=0 }41x+a2x,+L+an=0 (4-5) LLLLLLLLLLLL amx+am2x2+L+amnxn =0 若记 ean an La1n ex1ù e L ú e 422 A= eL L L din,x= Lú e Mu ú e u ěml am2 L amn ěxni 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 设有齐次线性方程组 若记 （4-5） 一、齐次线性方程组解的性质

线性代数第四章 则上述方程组(4-5)可写成向量方程 Ax=0 (4-6) 若x1,x2,L,xn为方程(4-5)的解，则 ex1ù eú x= èx2i eMú eú exn 为方程(4-6)的解向量，也就是方程 (4-5)的解向量. 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 则上述方程组（4-5）可写成向量方程

线性代数第四章 i a心+a252+L+anxn=0 a211+a222+L+42nxn=0 (4-5) Ax=0(4-6) LLLLLLLLLLLL am+am22+L+amn=0 性质4.2.1设x1x,是方程组(4-5)的解向量， 则x,+x,也是方程组(4-5)的解向量. |A(G,+2)=,+A化=0故x=x+x,也是Ax=0的解 性质4.2.2设是方程组(4-5)的解向量，1是任意数， 则1x也是方程组(4-5)的解向量. IQA(x,)=1A(c)=10=0.11x也是方程组(4-5)的解向量] 推广：设x1心2,4，心n,是方程组(4-5)的解向量，11，l2,41m 是任意数，则l心，+1心2+H+1m,xn,仍是方程组(4-5)的解向量. 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 （4-5）

线性代数第四章 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间.它是”的一个子空间. 如果方程组(4-5)有非零解，由性质4.2.1、4.2.2知， 它一定有无穷多非零解要求出(4-5)的所有解，只需 求出解空间的一个基就行了. 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间. 它是R n的一个子空间. 如果方程组(4-5)有非零解，由性质4.2.1、4.2.2知， 它一定有无穷多非零解.要求出(4-5)的所有解，只需 求出解空间的一个基就行了

线性代数第四章 二、基础解系及其求法 设X1X2,L,Xm是AX=0E 的解，满足 (1)x1心2，L心m,线性无关 【2)AX=0的任一解都可以由飞1X2,Lxm, 线性表示。 则称X1心2，L心m,是AX=0的一个基础解系。 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 二、基础解系及其求法 设 是 的解，满足 线性无关； 的任一解都可以由 线性表示。 则称 是 的一个基础解系

线性代数第四章 定理：设A是m'n矩阵，如果r(A)=r<n, 则齐次线性方程组AX=0 的基础解系存在， 且每个基础解系中含有-r个解向量。 证明 设线性方程组(4-5)系数矩阵A的秩为，不妨假设A的 前个列向量线性无关，于是A的行最简形为 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A的 前r个列向量线性无关，于是A的行最简形为 定理： 设 是 矩阵，如果 则齐次线性方程组 的基础解系存在， 且每个基础解系中含有 个解向量。 证明

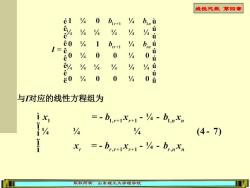
线性代数第四章 é1 4 0 birtt 4 bnù 4 4 4 为 e0 4 1 4 I= bin 4 0 0 4 0ú 44 % h u e 0 0 4 0 i 与对应的线性方程组为 ix =-b+1x,+1-4-bn七 4 4 (4-7) II X,=-b+1x,+1-4-bnXn 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 与I对应的线性方程组为

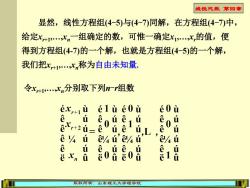
线性代数第四章 显然，线性方程组(4-5)与(4-7)同解，在方程组(4-)中， 给定x+1vXm一组确定的数，可惟一确定x1,.X,的值，便 得到方程组(4-7)的一个解，也就是方程组(4-5)的一个解， 我们把+1，.比m称为自由未知量。 令x+1n分别取下列-r组数 ex,+1ùé1ùé0ù e0ù e ú èxr+2i=ě0ú，e ú，L e ú ehúe4ú'eh eh4ú e ú e。 ú ě0iě00 S 版权所有：山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 显然，线性方程组(4-5)与(4-7)同解，在方程组(4-7)中， 给定xr+1,.,xn一组确定的数，可惟一确定x1 ,.,xr的值，便 得到方程组(4-7)的一个解，也就是方程组(4-5)的一个解， 我们把xr+1,.,xn称为自由未知量. 令xr+1,.,xn分别取下列n-r组数

由(4-7)依次可得 线性代数第四章 e.x,ù e-bi.r e-by.2 ù 4 e 4 w 4 i ex,ǘ 8b,+2 从而得到(4-7)也就是(4-5)的n-r个解 b1+20 4 ú b b. ú , X1= ee 1 X2 0 公 Xn-r 0 ú eee 0 sa3s 0 <O< 1 0 4 o 4 55 0 H 3S 版权所有： 山东理工大学理学院

线性代数 第四章 版权所有：山东理工大学理学院 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解