《高等数学》课程教学资源（PPT课件）第一章课件

Advanced mathematics 第一章 高等数学 函数、连续与极限 人民邮电出版社

1 第一章 函数、连续与极限 第一章 人民邮电出版社 Advanced mathematics 高等数学 函数、连续与极限

第一章 内容导航 第一节集合与函数 第二节数列的极限定义与计算 第三节函数的极限定义与计算 第四节极限的证明与性质 第五节两个重要极限 第六节无穷小的概念与比较 第七节函数的连续性及其性质

2 第一章 函数、连续与极限 第一章 内容导航 第二节 数列的极限定义与计算 第三节 函数的极限定义与计算 第四节 极限的证明与性质 第五节 两个重要极限 第六节 无穷小的概念与比较 第七节 函数的连续性及其性质 第一节 集合与函数

课前导读 集合 具有某种确定性质的对象的全体称为集合（简称集），组成集合的个别 对象称为集合的元素。习惯上，用大写英文字母A,B,C,.表示集合， 用小写字母a,b,c,.表示集合的元素.a∈A表示a是集A的元素 (读作a属于A),a生A表示a不是集A的元素（读作a不属 于A).集合按照元素的个数分为有限集和无限集，不含任何元素的 集合称为空集，记为⑦·

课 前 导 读 集 合 习惯上，用大写英文字母 表示集合， 用小写字母 表示集合的元素. A B C , , , abc , , , a 3 具有某种确定性质的对象的全体称为集合（简称集），组成集合的个别 对象称为集合的元素. a A  a A a A a A  A a A 表示 是集 的元素 （读作 属于 ）， 表示 不是集 的元素（读作 不属 于 ）.  集合按照元素的个数分为有限集和无限集 ，不含任何元素的 集合称为空集，记为

课前导读 函数 设x和y是两个变量，D是一个非空数集.如果按照某个法则f,对 每个数x∈D,变量y总有唯一确定的值与之对应，则称此对应法则侧f 为定义在D上的函数，与x对应的值y称为f在x处的函数值，记 作f(x),即y=f(x).变量x称为自变量，y称为因变量.数集D称为 定义域，W={yy=f(x),x∈D}称为函数的值域

课 前 导 读 函 数 4 设 x 和 y 是两个变量， D 是一个非空数集. f x D y f D 如果按照某个法则 ，对 每个数 ，变量 总有唯一确定的值与之对应， 则称此对应法则 为定义在 上的函数， 与 对应的值 称为 在 处的函数值， 记 作 ，即 . x y f x f x( ) y f x = ( ) 变量 称为自变量， 称为因变量. 数集 称为 定义域， 称为函数的值域. x y D W y y f x x D = =   ( ), 

集合的概念 第一章函数、连续与极限 设A,B是两个集合， 若A的每个元素都是B的元素（见图1-1）， B 则称A是B的子集，记作AcB或BOA)· U ACB 读作“A包含于B”（或“B包含A”); 图1-1 若AcB且BpA,则称A与B相等，记作A=B; 对于任何集合A,规定0cA·

5 一、 集合的概念 第一章 函数、连续与极限 B A U A B  设 A B, 是两个集合， 图1-1 若 的每个元素都是 的元素(见图 1-1 )， 则称 是 的子集，记作𝐴 ⊂ 𝐵或 𝐵 ⊃ 𝐴）. A B A B 读作“ 包含于 ”（或“ 包含 ”）； 若 𝐴 ⊂ 𝐵 且 𝐵 ⊃ 𝐴 ，则称 与 相等，记作 ； 对于任何集合 ，规定 ⊂ 𝐴 . A B = A B B A A B A 

集合的概念 第一章函数、连续与极限 我们把自然数的全体组成的集合称为自然数集，记作N.由整数的全体 构成的集合称为整数集，记为Z.用Q表示全体有理数构成的有理数集，R 表示全体实数构成的实数集，显然有NcZcQcR 如果是正整数集，则记为Z+,负整数集记为Z-,以此类推 注：在本书中所讨论的数集除特别说明外均为实数集

6 一、 集合的概念 第一章 函数、连续与极限 我们把自然数的全体组成的集合称为自然数集，记作 . 由整数的全体 构成的集合称为整数集，记为 .   Q R     Z Q R 用 表示全体有理数构成的有理数集， 表示全体实数构成的实数集. 显然有 . 如果是正整数集，则记为 𝑍 + ，负整数集记为 𝑍 −，以此类推. 注： 在本书中所讨论的数集除特别说明外均为实数集

1.集合及其运算 第一章函数、连续与极限 集合的基本运算有四种：并、交、差、补 设A,B是两个集合 由同时包含于A与B的元素构成的集合（见图1-2)，称为A与B 的交集（简称交），记作A∩B,即A∩B={x|x∈A且x∈B}； 由包含于A或包含于B的所有元素构成的集合（见图1-3），称为A 与B的并集（简称并），记作AUB,即AUB={x|x∈A或x∈B}; B 图1-2 图1-3

7 1. 集合及其运算 第一章 函数、连续与极限 由同时包含于 与 的元素构成的集合（见图 1-2），称为 与 的交集（简称交），记作 ，即 且 ； A B A B A B x x A =  { | x B  } A B 由包含于 或包含于 的所有元素构成的集合（见图 1-3），称为 与 的并集（简称并），记作 A B ，即 A B x x A =  { | 或 x B  } ； A B A B 集合的基本运算有四种：并、交、差、补. 设 A B, 是两个集合. A A B B 图1-2 A A B  B 图1-3

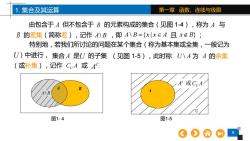
1.集合及其运算 第一章函数、连续与极限 由包含于A但不包含于B的元素构成的集合（见图1-4），称为A与 B的差集（简称差），记作A\B,即A\B={x|x∈A且xEB}; 特别地，若我们所讨论的问题在某个集合（称为基本集或全集，一般记为 U)中进行，集合A是U的子集（见图1-5)，此时称U八A为A的余集 (或补集)，记作CuA或AC A或CuA B A\B U 图1-4 图1-5

8 1. 集合及其运算 第一章 函数、连续与极限 由包含于 但不包含于 的元素构成的集合（见图 1-4），称为 与 的差集（简称差），记作 ，即 且 ； A B A B A B\ A B x x A \ { | =  x B  } 特别地，若我们所讨论的问题在某个集合（称为基本集或全集，一般记为 U ）中进行， A U c A C A 或 U A B 图1- 4 图1-5 A B\ 集合 A 是 U 的子集 （见图 1-5），此时称 为 的余集 （或补集），记作 或 . U A\ C AU C A A

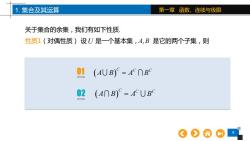
1.集合及其运算 第一章函数、连续与极限 关于集合的余集，我们有如下性质 性质1（对偶性质)设U是一个基本集，A,B是它的两个子集，则 01 (AUB)=A∩B9 02 (A∩B)=AUBO

9 1. 集合及其运算 第一章 函数、连续与极限 关于集合的余集，我们有如下性质. 性质1（对偶性质） 设 U 是一个基本集， A B, 是它的两个子集，则 ( ) C C C A B A B = ( ) C C C A B A B = 01 OPTION 02 OPTION

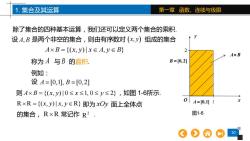
1.集合及其运算 第一章函数、连续与极限 除了集合的四种基本运算，我们还可以定义两个集合的乘积 设A,B是两个非空的集合，则由有序数对(x,y)组成的集合 A×B={(x,y)川x∈A,y∈B} 2 AxB 称为A与B的直积 B=0,2) 例如： 设A=[0,1],B=[0,2] 则A×B={(x,y)川0≤x≤1,0≤y≤2}，如图1-6所示 R×R={(x,y)川x,y∈R}即为xOy面上全体点 0A=0,1山1 的集合，R×R常记作R2. 图1-6 10

10 1. 集合及其运算 第一章 函数、连续与极限 1 2 x y O A = [0,1] B = [0, 2] A B 设 A B, 是两个非空的集合，则由有序数对 ( x y, ) 组成的集合 称为 与 的直积. 例如： A B x y x A y B  =   {( , ) | , } A B 设 A B = = [0,1], [0,2] 即为 面上全体点 的集合， 常记作 . R R {( , ) | , R}  =  x y x y xOy R R 2 R 图1-6 则 A B x y x y  =     {( , ) | 0 1, 0 2} ，如图 1-6所示. 除了集合的四种基本运算，我们还可以定义两个集合的乘积