《线性代数》课程教学课件(讲稿,B)第四章 线性方程组 §4.1 线性方程组的解的判别

第四章线性方程组 Ch4 线性方程组 ●§4.1线性方程组的解的判别 。§4.2齐次线性方程组的解的结构 ● §4.3非齐次线性方程组解的结构
第四章 线性方程组 Ch4 线性方程组 §4.2 齐次线性方程组的解的结构 §4.1 线性方程组的解的判别 §4.3 非齐次线性方程组解的结构

第四章线性方程组 §4.1线性方程组的解的判别 >一、引例 。二、线性方程组的解的判别方法
第四章 线性方程组 §4.1 线性方程组的解的判别 一、引例 二、线性方程组的解的判别方法

第四章线性方程组 、引例 n元线性方程组 01七1+412X2+.+41mXn=b1 a21X1+022X2+.+02mxn=b2 (4-1) mX1+m2大2++0mmXn=bnm 记 41 l12 1n 11 412 . ain A= L21 a22 ,A= 21 022 Ami Am2 Ami Am2
第四章 线性方程组 n 元线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b + + + = + + + = − + + + = 11 12 1 11 12 1 1 21 22 2 21 22 2 2 1 2 1 2 , n n n n m m mn m m mn m a a a a a a b a a a a a a b A A a a a a a a b = = 记 一、引例
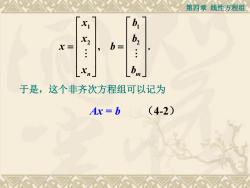
第四章线性方程组 b x= ·. ,b= Xn b 于是,这个非齐次方程组可以记为 Ax=b (4-2)
第四章 线性方程组 1 1 2 2 , . n m x b x b x b x b = = Ax = b (4-2) 于是,这个非齐次方程组可以记为

第四章线性方程组 由第二章的讨论可知,方程组(4-1)与增广矩阵 具有一一对应关系,对方程组进行加减消元相当 于对其增广矩阵进行初等变换,因此求解方程组 的问题就可以转化为矩阵的初等行变化问题. 一 般线性方程组的解可能会出现三种情况: 有唯一解、有无穷多解或无解
第四章 线性方程组 由第二章的讨论可知,方程组(4-1)与增广矩阵 具有一一对应关系,对方程组进行加减消元相当 于对其增广矩阵进行初等变换,因此求解方程组 的问题就可以转化为矩阵的初等行变化问题. 一般线性方程组的解可能会出现三种情况: 有唯一解、有无穷多解或无解

第四章线性方程组 线性方程组与几何联系 从几何角度考虑线性方程组 411x1+412x2=b1 021X1+42X2=b2 每一个方程均对应于平面上的一条直线 求解方程组,相当于求两条直线的交点:
第四章 线性方程组 线性方程组与几何联系 从几何角度考虑线性方程组 每⼀个方程均对应于平面上的⼀条直线. 求解方程组, 相当于求两条直线的交点. 11 1 12 2 1 21 1 22 2 2 a x a x b a x a x b + = + =
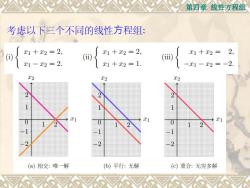
第四章线性方程组 考虑以下三个不同的线性方程组: x1+x2=2, x1+x2=2, x1+x2=2, ) () () C1-x2=2. x1+x2=1. -x1-x2=-2. T2 T2 (a)相交:唯一解 (b)平行:无解 (c)重合:无穷多解
第四章 线性方程组 考虑以下三个不同的线性⽅程组:

第四章线性方程组 两条直线之间的关系有三种情况:相交、平行、重合. 相应地,一个线性方程组的解,有下列三种情况: (1)唯一解 (2)无解 (3)无穷多解
第四章 线性方程组 两条直线之间的关系有三种情况: 相交、平行、重合. 相应地,⼀个线性方程组的解, 有下列三种情况: (1)唯一解 (2)无解 (3)无穷多解

第四章线性方程组 二、线性方程组解的判别 1 + X2 2x3 1, 2X1 一 X2 + 2x3 4, 例1:解线性方程组 X1 2X2 3, 4x 十 4x3 2
第四章 线性方程组 例1:解线性方程组 1 2 3 1 2 3 1 2 1 2 3 2 1, 2 2 4, 2 3, 4 4 2. x x x x x x x x x x x ++= − + = − = ++= 二、线性方程组解的判别

第四章线性方程组 解: 1 2 2 2 -1 2 4 0 -3 -2 2 (A,b)= 1 -2 0 3 3 -2 2 4 4 2 0 -3 -4 -2 1 1 2 1 2 0 -3 -2 2 0 1 2/3 -2/3 0 0 0 0 0 0 1 2 0 0 2 A 0 0¥0 0
第四章 线性方程组 解: 1 1 2 1 2 1 2 4 ( , ) 1 2 0 3 4 1 4 2 A b − = − 1 1 2 1 0 3 2 2 ~ 0 3 2 2 0342 − − − − −−− 1 1 2 1 0 3 2 2 ~ 0 0 0 0 0 0 2 4 − − − − 1 1 2 1 0 1 2/ 3 2/ 3 ~ 0 0 1 2 0 0 0 0 −
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学课件(讲稿,B)第四章 线性方程组 §4.2 齐次线性方程组.pdf
- 《线性代数》课程教学课件(讲稿,B)第四章 线性方程组 §4.3 非齐次线性方程组.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的运算 §3.1 矩阵的运算.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的运算 §3.2 逆矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的运算 §3.3 初等矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的运算 §3.4 分块矩阵.pdf
- 《线性代数》课程教学课件(PPT讲稿,B)第一章 行列式_1.1行列式的概念.ppt
- 《线性代数》课程教学课件(PPT讲稿)矩阵的秩及其求法.ppt
- 《数学分析》课程教学课件(讲义)实数完备性的若干证明.doc
- 《数学分析》课程教学资源(习题讲解)9不定积分.pdf
- 《数学分析》课程教学资源(习题讲解)10-11定积分广义积分.pdf
- 《数学分析》课程教学资源(习题讲解)12-13数项级数函数项级数.pdf
- 《数学分析》课程教学资源(习题讲解)14-15幂级数傅里叶级数.pdf
- 《数学分析》课程教学课件(讲稿)关于实数集完备性的基本定理.ppt
- 《数学分析》课程教学资源(文献资料)数学家简介.pdf
- 《高等数学》课程教学资源(作业习题)2019级文科高数.doc
- 《高等数学》课程教学资源(作业习题)高数A卷答案2019级.doc
- 《高等数学》课程教学资源(作业习题)作业——-函数与极限.doc
- 《高等数学》课程教学资源(作业习题)作业——-导数与微分.doc
- 《高等数学》课程教学资源(作业习题)作业——-微分中值定理与导数的应用.doc
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.6 正定二次型.pdf
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.5 二次型及其标准形.pdf
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.4 实对称矩阵的相似对角形.pdf
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.3 相似矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.2 方阵的特征值与特征向量.pdf
- 《线性代数》课程教学课件(讲稿,B)第五章 相似矩阵与二次型 §5.1 向量的内积与正交向量组.pdf
- 《线性代数》课程教学课件(PPT讲稿,B)第一章 行列式_1.3 n阶行列式的计算.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第一章 行列式_1.2 行列式的性质.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第一章 行列式_1.1 行列式的定义.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第二章 向量与矩阵 §2.4 矩阵的秩.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第二章 向量与矩阵 §2.3 向量组的线性相关性.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第二章 向量与矩阵 §2.2 向量及其线性运算.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第二章 向量与矩阵 §2.1 消元法与矩阵的初等变换.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第三章 矩阵的运算 §3.4 分块矩阵.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第三章 矩阵的运算 §3.3 初等矩阵.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第三章 矩阵的运算 §3.2 逆矩阵.ppt
- 《线性代数》课程教学课件(PPT讲稿,B)第三章 矩阵的运算 §3.1 矩阵的运算.ppt
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的理论_3-4分块矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的理论_3-3初等矩阵.pdf
- 《线性代数》课程教学课件(讲稿,B)第三章 矩阵的理论_3-2逆矩阵.pdf
