《高等数学》课程教学资源（PPT课件）第二章课件

Advanced mathematics 第二章 高等数学 元函数微分学及其应用 人民邮电出版社

1 第二章 一元函数微分学及其应用 第二章 人民邮电出版社 Advanced mathematics 高等数学 一元函数微分学及其应用

第二章 内容导航 第一节导数的概念及基本求导公式 第二节导数的计算法则 第三节微分的概念与应用 第四节微分中值定理及其应用 第五节泰勒中值定理 第六节函数的性态与图形 第七节导数的实际应用

2 第二章 一元函数微分学及其应用 第二章 内容导航 第二节 导数的计算法则 第三节 微分的概念与应用 第四节 微分中值定理及其应用 第五节 泰勒中值定理 第六节 函数的性态与图形 第七节 导数的实际应用 第一节 导数的概念及基本求导公式

课前导读 我们首先来看几个函数的图像 V X 0 图2-1 图2-2 图2-3 大家会发现，在x=x,处它们都是连续的，但是前两个函数的图 和后一个函数的图像相比，x=x,处有“角点”或“尖点”出现（见 图2-1、图2-2)，破坏了图形的美感和润滑度，而第三个函数相对来说 x=x处比较“光滑”（见图2-3)

课 前 导 读 我们首先来看几个函数的图像. 3 x 0 O x y x 0 O x y x 0 O x y 图 2-1 图 2-2 图 2-3 大家会发现，在 x x = 0 处它们都是连续的， 但是前两个函数的图 和后一个函数的图像相比， x x = 0 处有“角点”或“尖点”出现（见 图2-1、图2-2），破坏了图形的美感和润滑度，而第三个函数相对来说 处比较“光滑”（见图2-3） . 0 x x =

课前导读 那么究竟是什么原因会使图形有这样的差别呢？这就是这一章要研 究的内容.前面两个函数在x=x,处“导数”不存在，即不可导， 而第三个函数在x=x,处是“可导”的

课 前 导 读 4 前面两个函数在 x x = 0 处“导数”不存在，即不可导， 而第三个函数在 处是“可导”的. 0 x x = 那么究竟是什么原因会使图形有这样的差别呢? 这就是这一章要研 究的内容

割线与切线 第二章 一元函数微分学及其应用 在中学数学中，圆的切线可以定义为 “与圆只有一个交点的直线”（见图2-4) x2+y2=1 y=x2 图2-4 但对于一般曲线，这样定义是不合适的。例如， x=1 直线x=1与抛物线y=x只有一个交点（见图2- 5)，但显然不是实际意义下的切线： 图2-5 下面我们用极限的思想给出一般曲线的切线的定义

5 一、 割线与切线 第二章 一元函数微分学及其应用 在中学数学中， 圆的切线可以定义为 “与圆只有一个交点的直线” （见图2-4）. y O y O x 图 2-4 图 2-5 但对于一般曲线， 这样定义是不合适的。例如， 直线 与抛物线 只有一个交点（见图2- 5）， 但显然不是实际意义下的切线. x =1 2 y x = 2 y x = x =1 x 2 +y 2 =1 x 下面我们用极限的思想给出一般曲线的切线的定义

割线与切线 第二章 一元函数微分学及其应用 设曲线C:y=f(x),x∈I,在曲线C上取点M(,)及点N(x,y), 连接N,则N为过点M的割线，割线的倾角为p（见图2-6). 则割线MN的斜率为 tano=>-f(x)-f(x) y=f(x N x-Xo x-Xo M 图2-6 导数的几何意义 6

6 一、 割线与切线 第二章 一元函数微分学及其应用 设曲线 : ， ，在曲线 上取点 及点 ， 连接 ， 则 为过点 的割线， 割线的倾角为 （见图2-6）. C y f x = ( ) x I  C M x y ( 0 0 , ) N x y ( , ) MN MN M  0 0 0 0 ( ) ( ) tan y y f x f x x x x x  − − = = − − 则割线 MN 的斜率为 y O x C M N y f x = ( )  0 x x Δy Δx 图 2-6 导数的几何意义

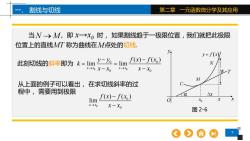
割线与切线 第二章一元函数微分学及其应用 当N→M,即x→x,时，如果割线趋于一极限位置，我们就把此极限 位置上的直线MT称为曲线在M点处的切线 y=f(x)/ 此刻切线的斜率即为k=limy-必=lim f(x)-f(x) →0X-X0x→0 x-Xo M 从上面的例子可以看出，在求切线斜率的过 程中，需要用到极限 lim f(x)-f(x.) x→x0 X-Xo 图2-6

7 一、 割线与切线 第二章 一元函数微分学及其应用 0 0 0 0 0 0 ( ) ( ) lim lim x x x x y y f x f x k → → x x x x − − = = − − 从上面的例子可以看出， 在求切线斜率的过 程中， 需要用到极限 0 0 0 ( ) ( ) lim x x f x f x → x x − − 当 ， 即 时， 如果割线趋于一极限位置，我们就把此极限 位置上的直线 称为曲线在 点处的切线. x→x N M → 0 MT M 此刻切线的斜率即为 y O x C M N y f x = ( ) T α 0 x x Δy Δx 图 2-6

二 导数的定义 第二章一元函数微分学及其应用 定义 设函数y=f(x)在x,的某个邻域内有定义，当x在x,处增量为△x (x。+△x在该邻域内)时，相应地，函数有增量△y=f(x+△x)-f(x)· 如果 lim Ay lim f(x+Ar)-f(%)=limf(x)-f(x) Ar-→0△x △r0 △x →0 x-Xo 存在，则称该极限为y=f(x)在点x,处的导数，记为 f),l或 8

8 二、导数的定义 第二章 一元函数微分学及其应用 定义 设函数 在 的某个邻域内有定义，当 在 处增量为 （ 在该邻域内）时，相应地， 函数有增量 . y f x = ( ) 0 x x 0 x x 0 x x +   = +  − y f x x f x ( 0 0 ) ( ) ( ) ( ) 0 0 0 0 0 0 0 ( ) ( ) lim lim lim x x x x y f x x f x f x f x  →  → → x x x x  +  − − = =   − 存在，则称该极限为 y f x = ( ) 在点 x0 处的导数，记为 f x ( 0 ) ， 0 x x y =  0 d d x x y x ， = 或 0 d ( ) d x x f x x = 如果

导数的定义 第二章一元函数微分学及其应用 这时也称函数y=∫(x)在点x,处可导 如果该极限不存在，称函数y=∫(x)在点x,处不可导. 特别地，如果m化=0时，也称函数y=f()在点x处的导数为无旁大 △r0△x

9 二、导数的定义 第二章 一元函数微分学及其应用 这时也称函数 y f x = ( ) 在点 处可导. 0 x 如果该极限不存在，称函数 y f x = ( ) 在点 处不可导 . 0 x 特别地，如果 时，也称函数 在点 处的导数为无穷大. 0 lim x y  → x  =   y f x = ( ) 0 x

二 导数的定义 第二章一元函数微分学及其应用 例如，对于函数y=x2,在点x=0处（见图2-7）， lim y =lim (0+△x)}-0 =lim△x=0,极限存在 Ar→0△x △x0 △x △x0 图2-7 y=x 而对于函数yx,在点x=0处（见图2-8）， lim Ay=lim 0+Ax-101-lim IAxl ar0△r 极限不存在. △x Ar0△x 由此可知，函数yx在x=0处不可导，而y=x2 图2-8 在x=0处导数为零，即 =0 10

10 二、导数的定义 第二章 一元函数微分学及其应用 例如，对于函数 在点 处（见图2-7）， 2 y x = , x = 0 0 lim x y  → x   ( ) 2 0 0 0+ 0 = lim lim 0 x x x x  →  → x  − =  =  ，极限存在. y x O 图 2-7 而对于函数 y x =| |, 在点 x = 0 处（见图2-8）， 0 lim x y  → x   0 0 |0+ | | 0 | | | = lim lim x x x x  →  → x x  −  =   ，极限不存在. O x y 图 2-8 y x =| | 2 y x = 由此可知，函数 y x =| | 在 x=0 处不可导， 2 y x = x=0 0 d 0 d x x y x = = 而 在 处导数为零，即