《线性代数》课程教学课件（讲稿，B）第五章 相似矩阵与二次型 §5.2 方阵的特征值与特征向量

第五章相似矩阵与二次型 §5.2方阵的特征值与特征向量 方阵的特征值与特征向量的概念 一二、方阵的特征值与特征向量的求法 三、方阵的特征值与特征向量的性质

第五章 相似矩阵与二次型 §5.2 方阵的特征值与特征向量 一、方阵的特征值与特征向量的概念 三、方阵的特征值与特征向量的性质 二、方阵的特征值与特征向量的求法

第五章相似矩阵与二次型 为什么要研究矩阵的特征值？ 本教材的核心是线性方程组的求解. 为了解决线性 方程组的求解，人们创造了行列式、矩阵等工具 这一章以矩阵为专门的研究对象.讨论矩阵的特征 值、矩阵的对角化等问题

第五章 相似矩阵与二次型 为什么要研究矩阵的特征值? 本教材的核心是线性方程组的求解. 为了解决线性 方程组的求解, 人们创造了行列式、矩阵等工具. 这⼀章以矩阵为专门的研究对象. 讨论矩阵的特征 值、矩阵的对角化等问题

第五章相似矩阵与二次型 特征值分析应用广泛： Google搜索； 图像处理：压缩、识别、去噪、修复、去模糊、融 合、变形等 汽车设计、建筑设计！

第五章 相似矩阵与二次型 特征值分析应用广泛: Google 搜索; 图像处理: 压缩、识别、去噪、修复、去模糊、融 合、变形等. 汽车设计、建筑设计

第五章相似矩阵与二次型 方阵的特征值与特征向量的概念 矩阵乘以向量，其功能是什么？ 给定4}引x=[日有w=[日 2 A:将x旋转，并改变其长度

第五章 相似矩阵与二次型 一、方阵的特征值与特征向量的概念 矩阵乘以向量, 其功能是什么? 1 2 0 2 = , , . 2 1 1 1 A x Ax       = =             给定 有 A x：将x旋转,并改变其长度

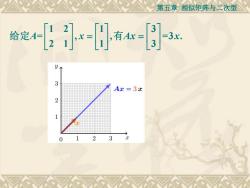
第五章相似矩阵与二次型 给定引x日有 =3x。 3 Ax=3x 2 3

第五章 相似矩阵与二次型 1 2 1 3 = , , =3 . 2 1 1 3 A x Ax x       = =             给定 有

第五章相似矩阵与二次型 可见，矩阵乘以一个向量，一般会将这个向量旋转 并改变其长度；但是对某些向量，只会在原方向或反 方向上伸长或缩短，或者说保持在原来的直线上.我 们对这种现象非常感兴趣：矩阵和这些数值、向量是 否存在某种内在的联系」

第五章 相似矩阵与二次型 可见, 矩阵乘以⼀个向量, ⼀般会将这个向量旋转, 并改变其长度; 但是对某些向量, 只会在原方向或反 方向上伸长或缩短, 或者说保持在原来的直线上. 我 们对这种现象非常感兴趣: 矩阵和这些数值、向量是 否存在某种内在的联系

第五章相似矩阵与二次型 方阵的特征值与特征向量的概念 定义5.2.1设A是n阶矩阵，若存在数元和非零向 量x,使得Ax=2x成立，则称数入为方阵A的特征 值，非零向量x称为A的对应于特征值2的特征向量， 说明：一个特征向量只能属于一个特征值， 但是一个特征值可能有多个特征向量

第五章 相似矩阵与二次型 5.2.1 . , A n x Ax x A x A     = 设 是 阶矩阵，若存在数 和非零向 量 使得 成立，则称数 为方阵 的 非零向量 称为 的对应于特 特 征值 的 征 值， 特 定 征向量 义 一个特征向量只能属于一个特征值， 但是一个特征值可能有多个特征向量. 一、方阵的特征值与特征向量的概念 说明：

第五章相似矩阵与二次型 方阵的特征值与特征向量的求法 阶方阵A的特征值，就是使齐次线性方程组 (A-2E)x=0有非零解的入值，即满足方程A-入E =0的入都是矩阵A的特征值

第五章 相似矩阵与二次型 , ( ) 0 , 0 . n A A E x A E A     − = − = 阶方阵 的特征值 就是使齐次线性方程组 有非零解的 值 即满足方程 的 都是矩阵 的特征值 二、方阵的特征值与特征向量的求法

第五章相似矩阵与二次型 由定义5.2.1得A-E=0 42 022-入 → =0 An2 Ann - 称以2为未知数的一元n次方程A-2E=0 为方阵A的特征方程， 记fA(2)=A-九E,它是的n次多项式， 称其为方阵A的特征多项式

第五章 相似矩阵与二次型 由定义5.2.1 0 得 A E − =  11 12 1 21 22 2 1 2 0 n n n n nn a a a a a a a a a    − −  = − 0 , n A E A 称以  为未知数的一元 次方程 − = 为方阵 的特征方程 ( ) , , . A f A E n A 记    = − 它是 的 次多项式 称其为方阵 的特征多项式

第五章相似矩阵与二次型 求特征值与特征向量的步骤： 1.解A-E=0求出2的值，即求特征值； 2.对每一个几，求方程组 (A-入E)x=O的基础解系， 即得到属于这个特征值的线性无关的特征向量 n-R(A-2E个

第五章 相似矩阵与二次型 1. 0 , 解 A E − =   求出 的值 即求特征值； 2. , ( ) A E O x  − =  对每一个 求方程组 的基础解系， 求特征值与特征向量的步骤： n –R(A–λE)个 即得到属于这个特征值的线性无关的特征向量