《线性代数》课程教学资源（PPT课件，A）3-1矩阵的运算

第三章矩阵的运算矩阵的运算Ch383.1矩阵的运算83.2逆矩阵83.3初等矩阵83.4分块矩阵

第三章 矩阵的运算 Ch3 矩阵的运算 §3.1矩阵的运算 §3.4分块矩阵 §3.2逆矩阵 §3.3初等矩阵

第三章矩阵的运算$ 3.1矩阵的运算矩阵的加法矩阵的数乘矩阵乘法矩阵转置方阵的行列式

第三章 矩阵的运算 §3.1 矩阵的运算 矩阵的加法 矩阵转置 矩阵的数乘 矩阵乘法 方阵的行列式

第三章矩阵的运算几种特殊的矩阵方阵：行数与列数相等的矩阵aa121na22a2n上三角形矩阵nxnnnbb21baB=下三角形矩阵nxn-bbhnin2nn

第三章 矩阵的运算 几种特殊的矩阵： 方阵：行数与列数相等的矩阵. 上三角形矩阵 11 12 1 22 2 n n n n nn a a a a a A a        =       下三角形矩阵 11 21 22 1 2 n n n n nn b b b B b b b        =      

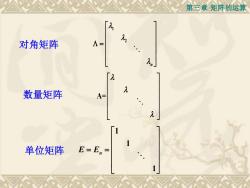
第三章矩阵的运算元元A=对角矩阵元2数量矩阵A=2E=E.单位矩阵=

第三章 矩阵的运算 对角矩阵 A=                1 2 n         =         数量矩阵 1 1 1 E En     = =         单位矩阵

第三章矩阵的运算零矩阵元素全是零的矩阵称为零矩阵.记作：000101L00000行矩阵只有一行的矩阵行向量就是行矩阵只有一列的矩阵。列向量就是列矩阵列矩阵一阶矩阵[a11] = a11同型矩阵行数与列数分别相等的矩阵称为同型矩阵

第三章 矩阵的运算 零矩阵 元素全是零的矩阵称为零矩阵.记作: O. 行矩阵 只有一行的矩阵. 行向量就是行矩阵. 列矩阵 只有一列的矩阵. 列向量就是列矩阵. 一阶矩阵 同型矩阵 行数与列数分别相等的矩阵称为同型 矩阵

第三章矩阵的运算矩阵相等：A=(aj)mn,B=(b,)mxng A=Bai, =(i=1,...,m;j= 1,..,n)30Sa=4,c=33444a335001丰44LaLaCC

第三章 矩阵的运算 ( ) , ( ) , ( 1, , ; 1, , ) A a B b A B a b ij m n ij m n ij ij i m j n = = =  =   = = 矩阵相等 :

第三章矩阵的运算一、矩阵加法设矩阵A=(aj,)mn,B=(bj)mn，称矩阵1、定义3.1.1 iC= (a;, +b,)mxn为矩阵A与矩阵B的和，记作C=A+B.注意：两个矩阵必须是同型矩阵才可以相加2、设矩阵A=(a）mxn，称矩阵(-a,)mxn为A的负矩阵记作-A,即-A=(-a;)mxn

第三章 矩阵的运算 一、矩阵加法 ( ) , ( ) ( ) . 3.1.1 ij m n ij m n ij ij m n A a B b C a b A B C A B    = = = + = + 设矩阵 ，称矩阵 1 和 为矩阵 与矩阵 的 记作 、定义 ， ( ) ( ) ( ) . ij m n ij m n ij m n A a a A A A a    = − − − = − 2、设矩阵 ，称矩阵 为 的 ， 记作 ，即 负矩阵 注意：两个矩阵必须是同型矩阵才可以相加

第三章矩阵的运算矩阵加法的性质：A,B,C,O均为m×n矩阵1. A+B=B+A2.(A+B)+C=A+(B+C)3. A+0=0+A=A4A+(-A)=(-A)+A=05.矩阵减法可定义为A-B=A+(-B)=(a -bjmxn

第三章 矩阵的运算 矩阵加法的性质： A, B,C , O均 为 m  n矩 阵 1. A + B = B + A 2. ( A + B ) + C = A + ( B + C ) 3 . A + O = O + A = A 4. A + ( − A ) = ( − A ) + A = O 5. ( ) ( ) A B A B a b − = + − = −ij ij m n 矩 阵 可 定 义 为 减 法

第三章矩阵的运算使得例1求矩阵X，23+X=解：01032X=12-1-130-3021

第三章 矩阵的运算 1 1 2 3 1 0 1 2 3 2 0 1 2 3 0 1 1 1 1 0 1 1 2 2 0 X X     − −     + = −             − − − 例 求矩阵 ，使得 解： 0 1 2 3 1 2 3 1 3 0 1 1 2 0 1 2 1 2 2 0 1 1 0 1 X     − −     = − −             − − − 1 3 1 4 1 0 0 3 2 1 2 1   − − −   = −       −

第三章矩阵的运算二、数与矩阵的乘法定义3.1.22是一个数,矩阵设矩阵A=(a)mxn，(a,)mn称为数与矩阵A的乘积，记作A或A,即A= AL =(Za,)mxn注：数乘矩阵与数乘行列式是显然是不同的

第三章 矩阵的运算 二、数与矩阵的乘法 ( ) , , ( ) ( ) 3.1.2 ij m n ij m n ij m n A a a A A A A a A            = = = 数 设矩阵 是一个数 矩阵 称为 记作 或 ， 即 与矩阵 ， 定 的乘积 义 注：数乘矩阵与数乘行列式是显然是不同的