《线性代数》课程教学资源（PPT课件，A）4-2齐次线性方程组

第四章线性方程组84.2齐次线性方程组齐次线性方程组的性质基础解系及其求法电-三、小结

第四章 线性方程组 三、小结 二、基础解系及其求法 一、齐次线性方程组的性质 §4.2 齐次线性方程组

第四章线性方程组一、齐次线性方程组解的性质设有齐次线性方程组ai +ai2X2 +...+ainXn = 0a21X + a22X2 + ... + a2nXn = 0(4-5)+amx,=0am1X,+am2X2+Xaua12aina21X2a222n若记 A=,x=aamlm2mn

第四章 线性方程组 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （4-5） 一、齐次线性方程组解的性质 11 12 1 1 21 22 2 2 1 2 , n n m m mn n a a a x a a a x A x a a a x             = =            

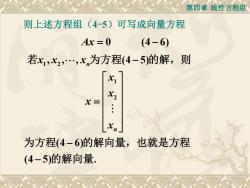
第四章线性方程组则上述方程组（4-5）可写成向量方程Ax = 0(4-6)若xi,X2,…,x,为方程(4-5)的解，则XiX2x=X为方程(4－6)的解向量，也就是方程(4-5)的解向量

第四章 线性方程组 则上述方程组（4-5）可写成向量方程 Ax = − 0 (4 6) 1 2 1 2 , , , (4 5) (4 6) (4 5) n n x x x x x x x −       =       − − 若 为方程 的解，则 为方程 的解向量，也就是方程 的解向量

第四章线性方程组性质4.2.1两个解向量的和仍然是解向量，即设,5,是方程组(4-5)的解向量，则 +5,也是方程组(4－5)的解向量证明只需证明 +5,满足方程组(4-6)即可: AE = 0, A5 = 0: A(5 + 5)= AS +A52 = 0故x=i+52也是Ax=0的解

第四章 线性方程组 1 2 1 2 , (4 5 4.2. ) (4 5 1 )     − + − 两个解向量的和仍然是解向量，即 设 是方程组 的解向量， 性质 则 也 是方程组 的解向量. 证明  A( 1 +  2 ) = A 1 + A 2 = 0  A 1 = 0, A 2 = 0 故 x 也是Ax 0的解. =  1 +  2 = 只需证明  1 2 + 满足方程组(4 6) − 即可

第四章线性方程组性质4.2.2一个解向量的倍数仍是解向量，即设是方程组（4一5)的解向量，入是任意数，则入也是方程组（4-5）的解向量证明 : A()= A()= 0=0.：.2也是方程组(4-5)的解向量性质4.2.3设51,52,.……,5,是方程组(4-5)的解向量,,...,是任意数，则+,+..+,仍是方程组(4-5)的解向量

第四章 线性方程组 (4 5) (4 5 . .2 ) 4 2     − − 一个解向量的倍数仍是解向量，即 设 是方程组 的解向量， 是任意数， 则 性质 也是方程组 的解向量. 证明 A A (    ) = = = ( ) 0 0.  − 也是方程组(4 5)的解向量 1 2 1 2 1 1 2 2 , , , (4 5) , , ( 4.2. 4 5) 3 s s s s              −  + ++ − 设 是方程组 的解向量， 是任意数，则 仍 是方程组 的 性质 解向量

第四章线性方程组二、基础解系及其求法如果方程组（4-5）有非零解，它一定有无穷多非零解1、基础解系设5,52…,5,是方程组（4-5）的一组解向量，若满足：1)线性无关；2)方程组的任意解向量都能由1,2.,5,线性表示；则称1,52,5,是方程组的基础解系

第四章 线性方程组 二、基础解系及其求法 如果方程组(4-5)有非零解，它一定有无穷多非零解. 1、基础解系 1)线性无关； 1 2 , , , - r 设    是方程组（4 5）的一组解向量，若满足：

第四章线性方程组2、存在性及求法定理：如果方程组（4-5)有非零解，它必有基础解系并且基础解系所含向量的个数为n一R(A)证明：设A经过初等行变换可化为：br+nbrr+rn1

第四章 线性方程组 2、存在性及求法 定理：如果方程组(4-5)有非零解，它必有基础解系， 并且基础解系所含向量的个数为 n R A − ( ). 证明： 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I + +               =            

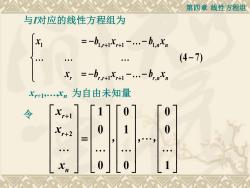
第四章线性方程组与I对应的线性方程组为Xi+1Xr+1 -...-b,1(4-7)=-bx.-bXPr,r+1Xr+1 -.r-nXr+1n为自由未知量x今r+10七r+2

第四章 线性方程组 1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x + + + +  = − −−     −  = − −−  与I对应的线性方程组为 xr+1,.,xn 为自由未知量 1 2 1 0 0 0 1 0 0 0 1 r r n x x x + +                   =                                   ， ， ， 令

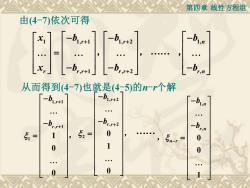
第四章线性方程组由（4-7)依次可得h-hx.1,r+1.r+1r.r+l,r+2从而得到(4-7)也就是(4-5)的n-r个解-b1,r+2-b1,+16-b,r+2-b,r+15 =00

第四章 线性方程组 1 1, 1 , 1 r r r r x b x b + +     −        =          −  ， 1, 2 , 2 r r r b b + +   −        −  ， 1, , n r n b b   −        −  ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b  + +   −        −   =              ， 1, 2 , 2 2 0 1 0 r r r b b  + +   −        −   =              ， 1, , 0 0 1 n r n n r b b  −   −        −   =              ，

第四章线性方程组下面证明引i,52,.…,5n-,是方程组的基础解系.Xr+!Xr+2首先由于所取的n-r个n-r维向量x000线性无关

第四章 线性方程组 1 2 , , , n r    下面证明  − 是方程组的基础解系. 1 2 1 0 0 0 1 0 0 0 1 r r n x x n r n r x + +       − −                                               首先由于 所取的 个 维向量 ， ， ， 线性无关