《线性代数》课程教学资源（PPT课件，A）行列式1.2 行列式的性质

第一章行列式$ 1.2行列式的性质行列式的性质二、 应用举例三、 代数余子式的性质

第一章 行列式 二、应用举例 一、行列式的性质 §1.2 行列式的性质 三、代数余子式的性质

第一章行列式行列式的性质一、性质1.2.1行列式与它的转置行列式相等la11a12aina21a22a2nD=.....anian2ann[a11a21ania12a22an2(或DTD'二..：aina2nann即D=D

第一章 行列式 性质1.2.1 行列式与它的转置行列式相等. 一、行列式的性质

第一章行列式性质1.2.2互换行列式的两行（列），行列式变号a13Iala121naans1snnduaInSsna0anQnnn2nnn推论1如果行列式有两行（列）完全相同，则此行列式为零

第一章 行列式 性质1.2.2 互换行列式的两行（列），行列式变号. 11 12 1 1 2 ln 1 2 1 2 . . . . . . . . . . . . . . . . . . . . . . . n l l s s sn n n nn a a a a a a a a a a a a 11 12 1 1 2 1 2 ln 1 2 . . . . . . . . . . . . . . . . . . . . . . . n s s sn l l n n nn a a a a a a a a a a a a 推论1 如果行列式有两行（列）完全相同，则 此行列式为零

第一章行列式性质1.2.3行列式的某一行（列）中所有的元素的中公因子k，可以提到行列式外面aa12ainalaina12ai2ailQkailkai2kainLinanlan2aanan21nnnn推论2若行列式中有一行（列）元素全为零中则此行列式为零推论3若行列式中有两行（列）元素成比例则此行列式为零

第一章 行列式 n n nn i i in n a a a ka ka ka a a a      1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a k      1 2 1 2 11 12 1 = 性质1.2.3 行列式的某一行（列）中所有的元素的 公因子k，可以提到行列式外面. 推论2 若行列式中有一行（列）元素全为零， 则此行列式为零． 推论3 若行列式中有两行（列）元素成比例， 则此行列式为零．

第一章行列式性质1.2.4(拆分性质）若行列式中某一行（列）的元素a,都可以分解为两元素b与c之和，即则该行列式可分解为相应的两个行列aj=b,+c(j=1,2,",n,1≤i≤n),式之和，即aan1aia12anbbiz + Ci2bin+Cinbin +CinCilCin+inanan2aaaaannnn2nln2nnnn

第一章 行列式 性质1.2.4(拆分性质 ) ( ) ( 1, 2, , ,1 ) ij ij ij ij ij ij a b c a b c j n i n = + =   若行 列 式 中 某一 行 列 的 元素 都可 以 分解为两元素 与 之和，即 ，则该行列式可分解为相应的两个行列 式之和，即 11 12 1 1 1 2 2 1 2 . . . . . . . . . . . n i i i i in in n n nn a a a b c b c b c a a a + + + 11 12 1 11 12 1 1 2 1 2 1 2 1 2 . . . . . . . . . . . . . . . . . . . . . . n n i i in i i in n n nn n n nn a a a a a a b b b c c c a a a a a a = +

第一章行列式性质1.2.5把行列式的某一列（行）的各元素乘以同一数然后加到另一列（行)对应的元素上去，行列式不变aa122(12aldn1nai + kaji+ka.+kaai2ailaLiri2inD=1di2aaLil11i1jnaaanlan2annnln2nn

第一章 行列式 性质1.2.5 把行列式的某一列（行）的各元素乘 以同一数然后加到另一列(行)对应的元素上去， 行列式不变． k  11 12 1 1 2 1 2 1 2 . . . . . . . . . . . . . . . . n i i in j j jn n n nn a a a a a a D a a a a a a = 11 12 1 1 1 2 2 1 2 1 2 . . . . . . . . . . . . . . . . n i j i j in jn j j jn n n nn a a a a ka a ka a ka a a a a a a + + + =

第一章行列式注：行列式的性质凡是对行成立的对列也同样成立

第一章 行列式 注：行列式的性质凡是对行成立的对列也同样成 立

第一章行列式二、应用举例1x 31-x 1-y 1-z例1设3=1,求D=4101117111 -z-y-X解：D=413+4131

第一章 行列式 二、应用举例 3 1 0 1 1 2 1 x y z = ， 1 1 1 4 1 3 1 1 1 x y z D − − − 例1 设 求 = 解： 1 1 1 4 1 3 4 1 3 1 1 1 1 1 1 x y z D − − − = +

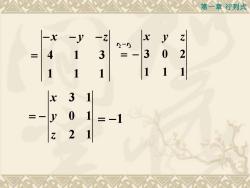
第一章行列式NX-z-x-y12-1332301A1１1131x0=-12Z

第一章 行列式 4 1 3 1 1 1 − − − x y z = 2 3 3 0 2 1 1 1 r r x y z − = − 3 1 0 1 2 1 x y z = − = −1

第一章行列式例2设多项式12312312-x2试求x)的根f(x)=5231239一x例3计算行列式bdaca+ba+b+ca+b+c+d0D=2a+b3a+2b+c4a+3b+ 2c+ da3a+b6a+3b+c10a+6b+3c+da

第一章 行列式 例2 设多项式 2 2 1 1 2 3 1 2 2 3 ( ) 2 3 1 5 2 3 1 9 x f x x − = − 试求f(x)的根. 例3 计算行列式 2 3 2 4 3 2 3 6 3 10 6 3 a b c d a a b a b c a b c d D a a b a b c a b c d a a b a b c a b c d + + + + + + = + + + + + + + + + + + +