《线性代数》课程教学资源（PPT课件，A）3-4分块矩阵

第三章矩阵的运算$ 3.4分块矩阵分块矩阵的概念二、分块矩阵的运算三、矩阵乘法的几种分块方法四、分块对角矩阵

第三章 矩阵的运算 一、分块矩阵的概念 二、分块矩阵的运算 四、分块对角矩阵 §3.4 分块矩阵 三、矩阵乘法的几种分块方法

第三章矩阵的运算一、分块矩阵的概念定义1设A是一个矩阵，在A的行或列之间加上一些线，把这个矩阵分成若干小块：用这种方法被分成若千小块的矩阵叫做一个分块矩阵.每一小块称为A的子块，每一个分块的方法叫做A一种分法a13a4anla12a15aa.(23a(2)222425例如A=(134(3)(132133(135AA5a41a143AuA13A12则A可记作2A,A23A

第三章 矩阵的运算 一、分块矩阵的概念 定义1 设A是一个矩阵，在A的行或列之间加上一 些线，把这个矩阵分成若干小块．用这种方法被分 成若干小块的矩阵叫做一个分块矩阵.每一小块称 为A的子块，每一个分块的方法叫做A一种分法. 例如 31 32 3 11 3 13 14 23 24 1 41 42 5 25 34 43 4 12 2 35 1 4 5 22 4 a a a a a a a a a a a a a a a a a a a A a       =       则A可记作 21 1 12 3 1 2 2 13 A 2 A A A A A   A =    

第三章矩阵的运算特殊分法设矩阵 A=(aj)snAA1.按行分块A=其中 A, =(ai,aiz,",ain)i =-1,2,..,s.ajanj2.按列分块=(A,Az,",An),其中 A, =j= 1,2,...,n.nj

第三章 矩阵的运算 特殊分法 设矩阵 ( ) , A a = ij s n 2.按列分块 A A A A = ( 1 2 , , , n ) ，其中 1 2 , j j j nj a a A a       =         j n = 1,2, , . 1.按行分块 1 2 , s A A A A     =         其中 1 2 ( , , , ), A a a a i i i in = i s = 1,2, ,

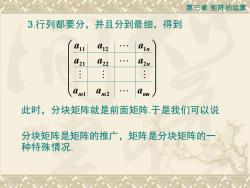
第三章矩阵的运算得到3.行列都要分，并且分到最细，anl012111a21a22a2naamlm2mn此时，分块矩阵就是前面矩阵.于是我们可以说分块矩阵是矩阵的推广，矩阵是分块矩阵的一种特殊情况

第三章 矩阵的运算 3.行列都要分，并且分到最细，得到               m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 此时，分块矩阵就是前面矩阵.于是我们可以说 分块矩阵是矩阵的推广，矩阵是分块矩阵的一 种特殊情况

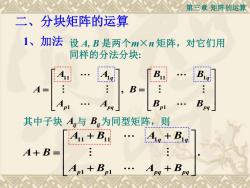
第三章矩阵的运算二、分块矩阵的运算1、加法设A.B是两个mXn矩阵，对它们用同样的分法分块：B,BAA1111aB=4=BBIDqq A,与 B,为同型矩阵，则其中子块+ BAl1 + B,49qA+B=+B+BV1pqq

第三章 矩阵的运算 11 1 11 1 1 1 , q q p pq p pq A A B B A B A A B B         = =             1、加法 设 A, B 是两个m×n 矩阵，对它们用 同样的分法分块: 二、分块矩阵的运算 11 11 1 1 1 1 . q q p p pq pq A B A B A B A B A B   + +   + =     + +   其中子块 Aij 与 Bij 为同型矩阵，则

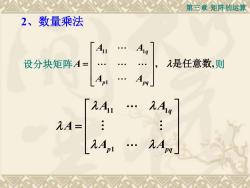
第三章矩阵的运算2、数量乘法2是任意数,则设分块矩阵A=pq2Au2AL2A=2AAq

第三章 矩阵的运算 2、数量乘法 设分块矩阵 11 1 1 , , q p pq A A A A A      =       是任意数 则 11 1 1 q p pq A A A A A          =      

第三章矩阵的运算把矩阵 A=(aik)mxs,B=(b;)xp分块成3、乘法B.1BuB=二.BBtq其中A,1,Ai2…,A,的列数分别等于Bt,B2j"B,的行数,那末AB =CCplpq其中C, -ZAiBi(i=-1,., ;j-1,.,)

第三章 矩阵的运算 11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B         = =             其 中 的 列 数 分 别 等 于 的 行 数 那 末 ( ) 11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q =     =       其 中 = = =  3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m s kj s p   分块成

第三章矩阵的运算注意：1当左边分块矩阵的列的分块方法和右边矩阵的行的分块方法一致时，分块矩阵才可以相乘2、两个分块矩阵的乘积分块矩阵的行数和列数分别等于左面分块矩阵的行数和右边分块矩阵的列数3.分块矩阵的第行第列的元素等于左边分块矩阵的第行子块与右边分块矩阵的第列子块对应相乘求和即有Ci, = A,Br, +...+ Ai,Bpjp

第三章 矩阵的运算 注意： 1、当左边分块矩阵的列的分块方法和右边矩阵 的行的分块方法一致时，分块矩阵才可以相乘. 2、两个分块矩阵的乘积分块矩阵的行数和列 数分别等于左面分块矩阵的行数和右边分块矩 阵的列数. 3.分块矩阵的第i行第j列的元素等于左边分块矩 阵的第i行子块与右边分块矩阵的第j列子块对应 相乘求和,即有 Ci j = Ai1 B1 j ++ Ai pBp j

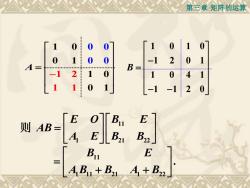
第三章矩阵的运算00007000-120B :=02110A福011E0BE11则 AB=B22B21AEB1EA +B,A,B., + B,20

第三章 矩阵的运算 1 2 1 1 0 0 1 1 0 0 0 0 1 0 0 1 A     =         − 1 0 1 0 1 2 0 1 1 0 4 1 1 1 2 0 B     − =         − − 11 1 21 22 E O B E AB A E B B     =         则 11 1 11 21 1 22 . B E A B B A B   =     + +

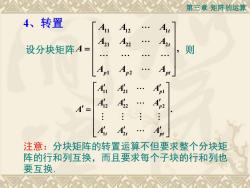
第三章矩阵的运算4、转置AnA2AA21A22A2则设分块矩阵A=AAnptA'AA'2A'DAztA'tADt注意：分块矩阵的转置运算不但要求整个分块矩阵的行和列互换，而且要求每个子块的行和列也要互换

第三章 矩阵的运算 11 21 1 12 22 2 1 2 . p p t t pt A A A A A A A A A A              =            设分块矩阵 11 12 1 21 22 2 1 2 , t t p p pt A A A A A A A A A A       =       则 4、转置 注意：分块矩阵的转置运算不但要求整个分块矩 阵的行和列互换，而且要求每个子块的行和列也 要互换