《高等数学》课程教学资源（PPT课件）第十章 重积分 10-03 第三节 三重积分

第三节三重积分、三重积分的概念二、 三重积分的计算三、小结 思考题

一、三重积分的概念 二、三重积分的计算 三、小结 思考题 第三节 三重积分

三重积分的概念引例：设在空间有限闭区域2内分布着某种不均匀的物质，密度函数为u(x,y,z)EC,求分布在Q内的物质的质量M解决方法：类似二重积分解决问题的思想，采用可得“分割，求和，取极限”Snu(5k,Nk,Sh)AvkM = lim△Vk2-→0k=1(5k,nkSk)

一、三重积分的概念 类似二重积分解决问题的思想, 采用 ( , , ) k k k k     v  ( , , ) k k k    k v 引例: 设在空间有限闭区域内分布着某种不 均匀的物质, ( , , ) , x y z C  求分布在 可得 1 n k= M = lim →0 “分割, 求和, 取极限” 解决方法: 内的物质的质量M. 密度函数为

1.三重积分的定义设f(x,y,z)是空间有界闭区域2上的有界函数将闭区域2任意分成n个小闭区域Avi,Av2,...Av其中表示第个小闭区域也表示它的体积在每个△v,上任取一点;,ni,5),作乘积f(S,n;,S,)Av,(i = 1,2...,n), 并作和(5,n;,5,)Av,如当各小闭区域直径中的最大值i=1

是空间有界闭区域Ω上的 如当各小闭区域直径中的最大值 在每个 i v ( , , ), i i i    ( , , ) ( 1,2 , ), i i i i f v i n     = 1 ( , , ) . n i i i i i f v    =   1 2 , , n    v v v 将闭区域Ω任意分成n个小闭区域 其中 i v 并作和 作乘积 f x y z ( , , ) 有界函数. 表示第i个小闭区域,也表示它的体积. 上任取一点 1. 三重积分的定义 设

几趋于零时这和的极限总存在，则称此极限为函数f(x,J,z)在闭区域Q上的三重积分JJ f(x, ,z)dv记为QZ(5i,n,5.)AvV;JJ f(x, ,z)a =lim)即1-→0i-12体积元素

记为 函数 f x y z ( , , ) 趋于零时这和的极限总存在, 0 1 lim ( , , ) n i i i i i f v     → = =    则称此极限为 在闭区域Ω上的三重积分. ( , , )d Ω f x y z v  即 ( , , )d Ω f x y z v  体积元素

在直角坐标系中，如果用平行于坐标面的平面来划分Q，则△v,=△x;Ayk△zi三重积分记为nZf(5i,n;,5.)Av;.Tf(x, y,z)dxdydz= lim1-0i-12其中 dxdydz叫做直角坐标体系中的体积元素

三重积分记为 f x y z dxdydz ( , , )   0 1 lim ( , , ) n i i i i i f v     → = =   . 的平面来划分, 在直角坐标系中，如果用平行于坐标面 . i j k l 则  =    v x y z 其中 dxdydz 叫做直角坐标体系中的体积元素

2.三重积分存在性当f(x,y,z)的三重积分存在性时，称f(x,y,z)在2上是可积的连续函数一定可积3.三重积分的几何意义设被积函数f(x,y,z)=1,则区域V的体积为V = JJ 1 . dv

设被积函数 f x y z ( , , ) 1,  1 d V V v =   连续函数一定可积 则区域V 的体积为 在Ω上是可积的. f x y z ( , , ) 的三重积分存在性时, f x y z ( , , ) 2. 三重积分存在性 3.三重积分的几何意义 当 称

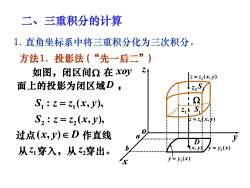
二、 三重积分的计算1.直角坐标系中将三重积分化为三次积分方法1．投影法（“先一后二”）Z如图，闭区间Ω 在xoyz=zz(x,y)面上的投影为闭区域D，Z2S一!QS, : z=zi(x,y),sS, : z = z(x, y),z=z(x,)0过点xV)ED作直线ayDh(x,ye= y2(x)从Z穿入，从Z穿出。y= yi(x)X

1. 直角坐标系中将三重积分化为三次积分． 二、三重积分的计算 x y z o  D 1 z 2 z S2 S1 1 z z x y = ( , ) 2 z z x y = ( , ) a b 1 y y x = ( ) 2 ( , ) x y y y x = ( ) 1 1 2 2 : ( , ), : ( , ), S z z x y S z z x y = = 方法1. 投影法 (“先一后二”) 如图，闭区间 在 面上的投影为闭区域 ，  xoy D 过点 ( , ) x y D  作直线 从 z1 穿入，从 z2 穿出

先将x,看作定值，将f(x,y,z)只看作z的函数，则z2(x,y)F(x,y) =f(x, y,z)dzz(x,y)计算F(x,J)在闭区D上的二重积分z2(x,y)JJj[ F(x, J)do = ]f(x, y,z)dzjdo.zi(x,y)DD: D: i(x)≤y≤yz(x), a≤x≤b,得

2 1 ( , ) ( , ) ( , ) ( , , ) z x y z x y F x y f x y z dz =  2 1 ( , ) ( , ) ( , ) [ ( , , ) ] . z x y z x y D D F x y d f x y z dz d   =    1 2 D y x y y x a x b : ( ) ( ), ,     得 先将 看作定值，将 只看作 的 函数，则 x y, f x y z ( , , ) z 计算 F x y ( , ) 在闭区D上的二重积分

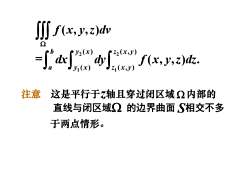
JJ f(x, y,z)dv2万y2(x)z2(x,y)dxdyf(x, y,z)dz.Ji(x)aZi(x,y注意这是平行于7轴且穿过闭区域Q内部的直线与闭区域Q的边界曲面S相交不多于两点情形

f x y z dv ( , , )  =  2 2 1 1 ( ) ( , ) ( ) ( , ) ( , , ) . b y x z x y a y x z x y dx dy f x y z dz    注意 这是平行于 轴且穿过闭区域 内部的 直线与闭区域 的边界曲面 相交不多 于两点情形。 z   S

I = [ f(x, y,z)dxdydz为例1化三重积分O三次积分，其中积分区域Q为由曲面=x2+2y2及z=2－x2所围成的闭区域分析解这种题的一般步骤是：先画出积分域的草图，找出积分域在坐标面上的投影域；其次列出所要积分次序的联立不等式；最后写出三次积分的表示式

例 1 化三重积分 I f x y z dxdydz ( , , )  =  为 三次积分，其中积分区域为由曲面 2 2 z x y = + 2 及 2 z x = −2 所围成的闭区域. 分析 解这种题的一般步骤是：先画出积分域的草图 ，找出积分域在坐标面上的投影域；其次列出所要积 分次序的联立不等式；最后写出三次积分的表示式