《高等数学》课程教学资源（PPT课件）第九章 多元函数微分法及其应用 9-6 第六节 多元函数微分学的几何应用

第六节多元函数微分学的几何应用一元向量值函数及其导数空间曲线的切线与法平面曲面的切平面与法线■小结思考题

第六节 多元函数微分学 的几何应用 ◼ 一元向量值函数及其导数 ◼ 空间曲线的切线与法平面 ◼ 曲面的切平面与法线 ◼ 小结 思考题

一、一元向量值函数及其导数(1)定义.设数集 DC R则称 f:D→R"为一元向量值(或矢量)函数，通常记为 π= f(t),te D或π= A(t),tε Dt称为自变量其中数据集D称为函数的定义域，产称为因变量下面以n=3为例，进行讨论

一、一元向量值函数及其导数 (1)定义.设数集 D R  ， 则称 : n f D R → (或矢量)函数，通常记为 为一元向量值 其中数据集D称为函数的定义域， r f t t D r t t D =  =  ( ) , A( ) , 或 t 称为自变量, r 称为因变量. 下面以n=3为例，进行讨论

若π=f(t),te D或产= A(t),t D,在O,直角系中的三个坐标分别用Ax(t),A,(t),A,(t)表示因此 A()的坐标表示式:Ax(t)i + Ay(t)j + Az(t)kA(l) =注：一个向量值函数和三个有序的数量函数（坐标）构成了一一对应的关系

中的三个坐标分别 用A (t), A (t), A (t)表示, x y z 因此 A(t) 的坐标表示式： A(t) = Ax t i Ay t j Az t k    ( ) + ( ) + ( ) 注：一个向量值函数和三个有序的数量函数（坐 标）构成了一一对应的关系. ( ) , A( ) , xyz 若 r f t t D r t t D O =  =  或 ，在 直角系

(2)终端曲线将A(）的起点取在坐标原点，当t变化时，A(）的终点M就描绘出一条曲线厂称该曲线为A(t)的终端曲线，又叫该向量值函数的图形A= A(t), 即 A= Ax(t)i+Ay(t)j+Az(t)k称为该曲线的向量方程

A(t) 的终点M就描绘出一条曲线 ，称该曲线 为 A(t)的终端曲线， 又叫该 向量值函数的图形. (2) 终端曲线 将 的起点取在坐标原点，当 t 变化时， A= A = Ax t i Ay t j Az t k    ( ) + ( ) + ( ) 称为该曲线的向量方程. A(t)  A(t)，即

称起点在坐标原点，终点为M(x，y，z)的向量OM为点M的向径，常用 π表示：-oM =xi +yi+ zkA()实际就当A(t）的起点取在坐标原点时，因此 Ax(t), Ay(t),Az(t)是终点M(x,y，z)的向量与x,y,z对应相等，即 x = Ax(t), y= A,(t),z = Az(t)称为曲线的以t为参数的参数方程

称起点在坐标原点，终点为M(x , y , z)的向量 OM 为点M的向径， r = OM xi yj zk    = + + 常用 r 表示: 是终点M(x , y , z)的向量. 因此 A (t), A (t), A (t) x y z 与 x , y , z对应相等， x A (t), y A (t),z A (t), 即 = x = y = z 当 A(t) 的起点取在坐标原点时， A(t) 实际就 称为曲线  的以 t 为参数的参数方程

注:A= Ax(t)i+A,(t)j+A,(t)k与x = Ax(t), y= A,(t),z= A,(t)一一对应例如，已知圆柱螺旋线的参数方程x=acos0,y=asino,z=bo则其向量方程为=acosoi+asini+bok(3）向量值函数的运算法则设 A(t) = Ax(t)i + Ay(t)j+ Az(t)k并假设等式右端所遇到的运算存在

注： A = Ax t i Ay t j Az t k    ( ) + ( ) + ( ) 与x A (t), y A (t),z A (t)一一对应. = x = y = z 例如，已知圆柱螺旋线的参数方程 x = acos , y = asin ,z = b 则其向量方程为 r a cos i a sin j b k = + +    (3) 向量值函数的运算法则 A(t) = Ax t i Ay t j Az t k    设 ( ) + ( ) + ( ) 并假设等式右端所遇到的运算存在

1) lim A(t) = lim A,(t)i + lim A, (t)i + lim A, (t)kt-→>tot-→>tot-→>tot-→>to特别 lim A(t)= A(to) 称A(t)在t = t连续t-→todAdA(t),(t)dA.dA. (t)(t12)1dtdtdtdtdA(t)A(t + △t) - A(t)其中limdtdt4t->03) dA(t) = A'(t)dt i + A',(t)dt j + A'(t)dt k

0 0 0 0 1) lim ( ) lim ( ) lim ( ) lim ( ) x y z t t t t t t t t A t A t i A t j A t k → → → → = + + ( ) ( ) ( ) ( ) 2) x y z dA t dA t dA t dA t i j k dt dt dt dt = + + 特 别 lim ( ) ( 0 ) 称 ( )在 0连 续 0 A t A t A t t t t t = = →    dt A t t A t dt dA t t ( ) ( ) lim ( ) 0    + − = →   其中 3 x y z ）dA( t ) A ( t )dt i A ( t )dt j A ( t )dt k = + +   

(4）向量值函数的求导法则设i=i(t),=(t)，p(t)可导，C为常向量，则2) [Ci(t)}' = Cu'(t)1) (C)= 03) [u(t)±(t)]}' =ü(t)±(t)4) [q(t)i(t)) = p'(t)i(t) +p(t)a(t)5) [u(t) ·(t)}' = u(t) ·(t)+i(t) ·(t)6) [u(t)xi(t) =ü(t)xi(t)+i(t)x(t)) i[q(t)} = @'(t)u[q(t))

(4) 向量值函数的求导法则 设u u t v v t t C = =  ( ), ( ) ( ) ， 可导， 为常向量，则 7) [ ( )] ( ) [ ( )] u t t u t       = 2)[ ( )] ( ) Cu t Cu t   = 5 [ ( ) ( )] ( ) ( ) ( ) ( ) ）u t v t u t v t u t v t  =  +     1) ( ) 0 C  = 3 [ ( ) ( )] ( ) ( ) ）u t v t u t v t  =    4 [ ( ) ( )] ( ) ( ) ( ) ( ) ）   t u t t u t t u t    = + 6 [ ( ) ( )] ( ) ( ) ( ) ( ) ）u t v t u t v t u t v t  =  +    

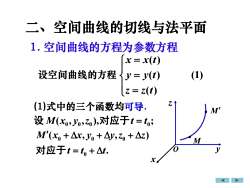
二、空间曲线的切线与法平面1.空间曲线的方程为参数方程x= x(t)(1)设空间曲线的方程y= y(t)z = z(t)Z(1)式中的三个函数均可导M'设 M(xo,Jo,z),对应于t =t;M'(x, + Axr, yo + Ay,zo + Az)My对应于t =t.+△t

设空间曲线的方程 (1) ( ) ( ) ( )      = = = z z t y y t x x t (1)式中的三个函数均可导. M • . ( , , ) 0 0 0 0 t t t M x x y y z z = +   +  +  +  对应于( , , ), ; 0 0 0 0 设 M x y z 对应于t = t • M 1. 空间曲线的方程为参数方程 二、空间曲线的切线与法平面 O x y z

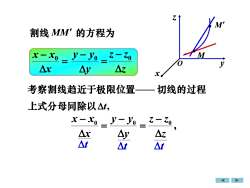
1M割线MM'的方程为M71x-xo20V-VoOyAxAzAyX考察割线趋近于极限位置切线的过程上式分母同除以△tx-xo -y- yoZ-ZoAyzAr△t△t△t

考察割线趋近于极限位置—— =  − x x x0 t t t 上式分母同除以 t, M • • M 割线 MM 的方程为 , 0 0 0 z z z y y y x x x  − =  − =  − =  − y y y0 z z z  − 0 切线的过程 O x y z