《高等数学》课程教学资源（PPT课件）第九章 多元函数微分法及其应用 9-7 第七节 方向导数与梯度

第七节方向导数与梯度1方向导数概念与计算公式1梯度概念与计算■数量场与向量场的概念■小结思考题

◼ 方向导数概念与计算公式 ◼ 梯度概念与计算 ◼ 小结 思考题 第七节 方向导数与梯度 ◼ 数量场与向量场的概念

一、方向导数概念与计算公式设有二元函数z=f(x,J),考虑函数在某点沿任何方向的变化率。1.方向导数的定义由点P发出的一条射线l，P射线是指有方向的半直线AyB在点P(x.y)附近于访向上取DAx一点P'(x +Ax,y+Ay)Ox记|PP'=p.即p = /(△x)2 +(Ay)

1. 方向导数的定义 设有二元函数 z = f (x, y), 沿任何方向的变化率． 考虑函数在某点 射线是指有方向的半直线, 由点P发出的一条射线l, 在 点P(x, y)附近于l方向上取 一点P(x + x, y + y), 记| PP |= . 即 ( ) ( ) , 2 2  = x + y 一、方向导数概念与计算公式  x y • l • P   x y O P

1f(P')- f(P)V定义如果极限limPP→PpOAyf(x+Ax,y+Ay)- f(x,y)B= limap-→0p Ar存在，则将这个极限值称为函数0x在点P沿方向的方向导数af即记为-aqaf(x+ △x, y + y) - f(x,y)limp-0p注方向导数是函数沿半直线方向的变化率

定义 如果极限  ( ) ( ) lim f P f P P P  − →   ( , ) ( , ) lim 0 f x + x y + y − f x y = → 存在,则将这个极限值称为函数 在点 P沿方向l的方向导数, 记为 , l f   即   ( , ) ( , ) lim 0 f x x y y f x y l f +  +  − =   → 注 方向导数是函数沿半直线方向的变化率.  x y P • l • P   x y O

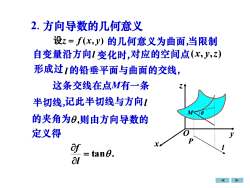
2.方向导数的几何意义设z=f(x,J)的几何意义为曲面,当限制自变量沿方向l变化时,对应的空间点(x,y,z)形成过1的铅垂平面与曲面的交线这条交线在点M有一条Z半切线，记此半切线与方向[MK6的夹角为,则由方向导数的0定义得yPaf1: tan0.al

x y z O 2.方向导数的几何意义 设z = f (x, y) 的几何意义为曲面,当限制 自变量沿方向 l 变化时,对应的空间点 (x, y,z) 形成过 l 的铅垂平面与曲面的交线, 这条交线在点M有一条 记此半切线与方向 l 的夹角为  , 则由方向导数的 = tan .   l f 半切线, 定义得 M l P 

注aff(x +△x, y+Ay)- f(x,y)= lim方向导数alp-→0O.p一定为正！是函数在某点沿任何方向的变化率aff(x+Ax,y)- f(x, y)lim偏导数axAxAr-→0aff(x, y+Ay)- f(x,y)limayAyAy-→0分别是函数在某点沿平行于坐标轴的直线的变化率，4x、4y可正可负！

  ( , ) ( , ) lim 0 f x x y y f x y l f +  +  − =   → ρ一定为正! x f x x y f x y x f x  +  − =    → ( , ) ( , ) lim 0 是函数在某点沿任何方向的变化率. 方向导数 偏导数 y f x y y f x y y f y  +  − =    → ( , ) ( , ) lim 0 分别是函数在某点沿平行于坐标轴的直线 的变化率. Δx、Δy可正可负！ 注

当函数f(x,J)在点P(x,y)的偏导数fx,f存在时，函数f(x,y)在点P(x,y)沿x轴正向e=(1,0)的方向导数存在,且值为f.事实上，aff(x+4x,y)- f(x,y)) = f.(x,y),limai4x4x-→>0+同理,函数f(x,J)在点P(x,y)沿y轴正向e,=(0,1)的方向导数存在，且值为f..事实上aff(x,y+4y)- f(x,y)2= f,(x,y),limaj4y4y-→0+

事实上, x f x x y f x y i f x    ( , ) ( , ) lim 0 + − =   → + f (x, y), = x 的方向导数存在, 事实上, y f x y y f x y j f y    ( , ) ( , ) lim 0 + − =   → + f (x, y), = y 当函数f (x, y) 函 数f (x, y)在 点P(x, y)沿x轴正向 e1 = (1,0) . x 且值为f 同理, 函 数f (x, y)在 点P(x, y)沿y轴正向 2 e = (0,1) 的方向导数存在, . y 且值为f x y 在点P(x, y)的偏导数 f , f 存在时

函数f(x,y)在点P(x,y)沿x轴负向(-1,0)aff(x+Ax,y)-f(x, )= -f(x,y),linai4r-→0-Ax函数f(x,y)在点P(x,J)沿y轴负向(0,-1)aff(x, y+Ay)- f(x,y)= -f,(x, ).linaj- AyAy-→0(afafafafafaf或当或反之，存在时(ayaiaxaiajaj.是否一定存在

=  if =  jf x f x x y f x y x −  +  − → −  ( , ) ( , ) lim0 y f x y y f x y y −  +  − → −  ( , ) ( , ) lim0 f ( x, y), = − x ( 0 , − 1 ) f ( x, y). = − y 函 数f (x, y)在 点P(x, y)沿x轴负向 (−1,0) 函 数f (x, y)在 点P(x, y)沿y轴负向 反之 , if if   当 或 存在时 , xf  是否一定存在     jf jf 或   yf

aff(x + Ax,y)- f(x, y)limaxAx4x→0例如，函数z=×2+在点(0,0)处沿方向=i的方向导数af_af(4x) + 02 - 0Axlimlim:1alai14x |Ax[4x/→04x→>0+(4x)~ + 0 - 0af4x4Z.但3limlimlimaxAxAxAx4x-→04x-→04x-→>0不存在。即z在(0,0)点的偏导数不存在

例如, 函数 z = x 2 + y 2在点(0, 0)处 沿方向 l i   = 的方向导数   ( , ) ( , ) lim 0 f x x y y f x y l f +  +  − =   → =   =   i f l f lim 1, 0 = = → + x x x    但 =   x f , | | lim 0 x x x    → = 不存在. 即z在(0, 0)点的偏导数不存在. | | ( ) 0 0 lim 2 2 | | 0 x x x    + − → x x x    ( ) 0 0 lim 2 2 0 + − → x f x x y f x y x f x    ( , ) ( , ) lim 0 + − =   → = → x zx x    0 lim

充分条件3.关于方向导数的存在定理设z=f(x,J)在点P(x,y)处可微,则函数在该点沿任意指定方向的方向导数都存在，且afaf _afcos β.cos α +alayax其中α、分别为方向与x轴、y轴正向的夹角证由于函数可微，则增量可表示为afaff(x+Axr,y+Ay)- f(x,y)EAr+Ay +o(p)axay两边同除以P,得到

证 由于函数可微, f (x + x, y + y) − f (x, y) = 得到 3. 关于方向导数的存在及计算公式 充分条件 定理 cos cos  . y f x f l f   +   =   设z = f (x, y)在 点P(x, y)处 在该点沿任意指定方向l 的方向导数都存在, 可微,则函数 且 其 中、分别为方向l与x轴 、y轴正向的夹角. 则增量可表示为 y o() y f x x f  +    +   两边同除以 

afafAx +Ay +o(p)f(x+Ax,y+Ay) - f(x,y) :axayafafAxo(p)Ayf(x+ Ax, y+ Ay) - f(x, y)ayaxppPPcos βcos α故有方向导数1ytP'aff(x+Ax,y+Ay) - f(x, y)OlimAyOalp-0paP△rafafcos β.cos α +0xaxay

cos cos  = +  +  −  f (x x, y y) f (x, y) 故有方向导数   ( , ) ( , ) lim 0 f x + x y + y − f x y → cos cos  . y f x f   +   = =   l f f (x + x, y + y) − f (x, y) = y o() y f x x f  +    +       y o( ) y x f x f +     +      y l   • P x • x y O P