《高等数学》课程教学资源（PPT课件）第十章 重积分 10-02 第二节 二重积分的计算法

第二节二重积分的计算法■利用直角坐标计算二重积分利用极坐标计算二重积分二重积分的换元法■小结思考题

◼ 利用直角坐标计算二重积分 ◼ 利用极坐标计算二重积分 ◼ 二重积分的换元法 ◼ 小结 思考题 第二节 二重积分的计算法

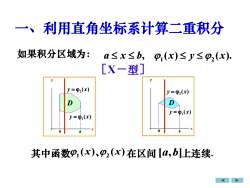
利用直角坐标系计算二重积分一、如果积分区域为：a≤x≤b,P (x)≤ y≤P(x)[X一型]yy=Φ2(x)y=P2(x)DDy=Φ(x)y=pi(x)ah11其中函数Pi(x)P2(x)在区间[a,b]上连续

如果积分区域为： a x b   , 1 2   ( ) ( ). x y x   其中函数 1 ( ) x 、  2 ( ) x 在区间 [ , ] a b 上连续. 一、利用直角坐标系计算二重积分 ［X－型］ ( ) 2 y =  x a b D ( ) 1 y =  x D a b ( ) 2 y =  x ( ) 1 y =  x

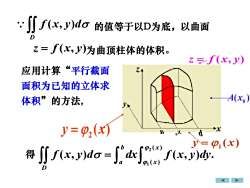
：f(x,J)d 的值等于以D为底，以曲面Dz=f(x,y)为曲顶柱体的体积。z =f(x,y)7.4应用计算“平行截面面积为已知的立体求A(x)体积”的方法，y=Φ2(x)+XDdXKy= Pi(x)P2(x)SJ f(x,y)do = J"得dxf (x, y)dy.(x)D

应用计算“平行截面 面积为已知的立体求 体积”的方法, a 0 x b z y x 0 A x( ) z f x y = ( , ) 1 y x =  ( ) 2 y x =  ( ) 2 1 ( ) ( ) ( , ) ( , ) . b x a x D f x y d dx f x y dy    = 得    ( , ) D f x y d z f x y = ( , ) 的值等于以D为底，以曲面 为曲顶柱体的体积

如果积分区域为：c≤≤d,(y)≤x≤2(y)[Y-型]yPl(y)x=x =0.()DDx=9P,(y)x =Φ2 (y)P2(y)J f(x,y)do =f(x,y)dx.P(y)D

( , ) ( , ) . ( ) ( ) 2 1    = D d c y y f x y d dy f x y dx    如果积分区域为： c y d   , 1 2   ( ) ( ). y x y   ［Y－型］ 2 x y =  ( ) 1 x y =  ( ) D c d c d 2 x y =  ( ) 1 x y =  ( ) D

X型区域的特点：穿过区域耳平行于轴的直线与区域边界相交不多于两个交点Y型区域的特点：穿过区域且平行于x轴的直线与区域边界相交不多于两个交点，若区域如图，则必须分割。在分割后的三个区域上分别使用积分公式 = + + .DDLD2D3

X型区域的特点： 穿过区域且平行于y轴的直 线与区域边界相交不多于两个交点. Y型区域的特点：穿过区域且平行于x轴的直 线与区域边界相交不多于两个交点. 若区域如图， D3 D2 D1 在分割后的三个区域上分别 使用积分公式 1 2 3 . D D D D = + +     则必须分割

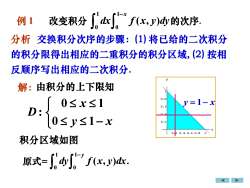
dx[~ f(x,y)dy的次序.例1改变积分分析交换积分次序的步骤：（1)将已给的二次积分的积分限得出相应的二重积分的积分区域，(2)按相反顺序写出相应的二次积分解：由积分的上下限知0.80≤x≤1y=1-x0.6D:[0≤y≤1-x0.20.40.60.8积分区域如图J,dyf," f(x, y)dx.原式=

y x = −1 例 1 改变积分 1 1 0 0 ( , ) x dx f x y dy −   的次序. 原式 1 1 0 0 ( , ) y dy f x y dx − =   . 解： 积分区域如图 分析 交换积分次序的步骤：(1) 将已给的二次积分 的积分限得出相应的二重积分的积分区域, (2) 按相 反顺序写出相应的二次积分. 由积分的上下限知 0 1 : 0 1 x D y x        −

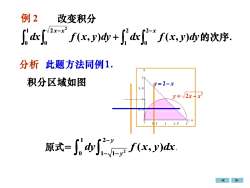
例 2改变积分2x-xdxf(x,y)dy的次序dxf(x, y)dy +J0分析此题方法同例1.积分区域如图V=2-x1.5V= /2x+x21.5原式=f(x, y)dx

y = 2 − x 2 y = 2x − x 例 2 改变积分     − − + x x x dx f x y dy dx f x y dy 2 0 2 1 2 0 1 0 ( , ) ( , ) 2 的次序. 原式 2 1 2 0 1 1 ( , ) y y dy f x y dx − − − =   . 分析 此题方法同例1. 积分区域如图

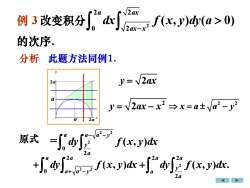
2a20例3改变积分dxf(x, y)dy(a > 0)的次序。分析此题方法同例1.y = V2axy=~2ax-x2 →x=a±ya-y原式f(x, y)dx2aI"dy/z f(x, y)dx.,y)dx +f(x,2a

例 3 改变积分 2 2 2 0 2 ( , ) ( 0) a ax ax x dx f x y dy a −    的次序. y ax = 2 分析 此题方法同例1. = 2 2 2 0 2 ( , ) a a a y y a dy f x y dx − −   原式 2 2 2 0 ( , ) a a a a y dy f x y dx + − +  2 2 2 2 ( , ) . a a y a a + dy f x y dx   2 y ax x = − 2 2 2  =  − x a a y a 2a 2a a

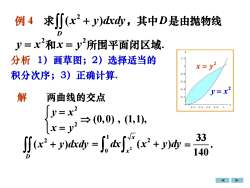
求[J(x2+y)dxdy，其中D是由抛物线例4D=2和x=所围平面闭区域分析 1）亚画草图；2)选择适当的X=积分次序；3）正确计算0.0.y=x?解两曲线的交点0.2.0.40.60.8-=→ (0,0) ， (1,1)33 dx/ (x? +[ (x? + y)dxdyVa140D

例 4 求 + D (x y)dxdy 2 ，其中D是由抛物线 2 y = x 和 2 x = y 所围平面闭区域. 解 2 2 (0,0) , (1,1), y x x y  =    = 2 ( ) D x y dxdy +  2 1 2 0 ( ) x x = + dx x y dy   33 . 140 = 2 y = x 2 x = y 2 y = x 2 x = y 两曲线的交点 分析 1）画草图；2）选择适当的 积分次序；3）正确计算

计算二重积分时，恰当的选取积分次序十分重要，它不仅涉及到计算繁简问题，文涉及到能否进行计算的问题凡遇如下形式积分：sinddx,{sinx'dx,[cosx'dx,Xax"dx, fe'dx, J x,o等等，一定要放在nx后面积分

计算二重积分时,恰当的选取积分次序十分重要, 它不仅涉及到计算繁简问题,又涉及到能否进行 计算的问题. 凡遇如下形式积分: d , sin x x x  d , 2 e x x  , ln d  x x 等等, 一定要放在 后面积分. sin d , 2 x x  cos d , 2 x x  d , 2 e x x  − e dx, x y 