《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-01 第一节 常数项级数的概念和性质

第一节常数项级数的概念和性质常数项级数的概念收敛级数的基本性质1收敛级数的必要条件■小结思考题

◼ 常数项级数的概念 ◼ 收敛级数的基本性质 ◼ 收敛级数的必要条件 ◼ 小结 思考题 第一节 常数项级数的概念和性质

为什么要研究无穷级数无穷级数是数和函数的一种表现形式是进行数值计算的有效工具（如计算函数值造函数值表）因无穷级数中包含有许多非初等函数故它在积分运算和微分方程求解时，也呈现出它的威力在自然科学和工程技术中，也常用无穷级数来分析问题，如谐波分析等

为什么要研究无穷级数 是进行数值计算的有效工具(如计算函数值、 出它的威力. 在自然科学和工程技术中,也常用无穷 无穷级数是数和函数的一种表现形式. 因无穷级数中包含有许多非初等函数, 故它在积分运算和微分方程求解时,也呈现 如谐波分析等. 造函数值表）. 级数来分析问题

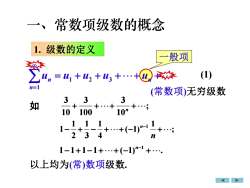
、常数项级数的概念1.级数的定义一般项紫(1)茶Zu, =u, +u, +u, +...+u)n=1(常数项)无穷级数333如1010010°3241-1+1-1+...+(-1)"-1 +...以上均为(常)数项级数

1. 级数的定义  = + + ++ +  = n n un u1 u2 u3 u 1 (常数项)无穷级数 一般项 如 ; 10 3 100 3 10 3 + ++ n + ; 1 ( 1) 4 1 3 1 2 1 1− + − ++ − −1 + n n 1 1 1 1 ( 1) . − + − ++ − n−1 + 以上均为(常)数项级数. (1) 一、常数项级数的概念

2.级数的收敛与发散概念无穷级数定义式(1)的含义是什么？按通常的加法运算一项一项的加下去永远也算不完，那么如何计算？称无穷级数(1)的前n项和nS, =u +u, +...+un, -Etui为级数(1)的部分和i=1这样,级数(1)对应一个部分和数列:S, =ui, S, =u, +u2, S, =ui+uz +us,Sn =u, +u, +...+un?

这样, 级数(1)对应一个部分和数列: sn = u1 + u2 ++ un = 称无穷级数(1)的 , 1 u1 s = , 2 u1 u2 s = + , 3 u1 u2 u3 s = + + , n u1 u2 un s = + ++ 2. 级数的收敛与发散概念 按通常的加法运算一项一项的加下去, 为级数(1)的  ,  无穷级数定义式(1)的含义是什么? 也算不完, 永远 那么如何计算? 前n项和  部分和. = n i ui 1

部分和数列可能存在极限.也可能不存在极限8定义主当n无限增大时,如果级数u,的部分和n=1数列s,有极限s，即lims,= s.则称无穷级数n>088u,收敛,这时极限叫做级数u,的和n=1n=1并写成s=u,+u,+L+u,+L8u.发散如果s,没有极限则称无穷级数》n=1即 lims,存在(不存在)台常数项级数收敛(发散)n-8

部分和数列可能存在极限,也可能不存在极限. 定义 当n无限增大时, s s, 数列 n有极限, 1  收敛  n= un . 1 这时极限 叫做级数 的 和  n= un s 1 2 n s u u u = + + + + L L 如果 没有极限, n s . 1 则称无穷级数 发 散  n= un 如果级数 的部分和  n=1 un lims s. n n = → 即 则称无穷级数 并写成 即 n  常数项级数收敛(发散). n s → lim 存在(不存在)

Zu, =u, +u, +u, +...+un, +... (l)n=1级数的敛散性它与部分和数列是否有极限是等价的对收敛级数(1),称差8ZuIn = S- Sn=un+1 +un+2 +.n+ii-1limr, = 0显然有为级数(1)的余项或余和n-00误差为rnl当n充分大时，Sn~s

n n r = s − s = un+1 + un+2 +   = = + i 1 un i lim = 0 → n n r 对收敛级数(1), 为级数(1)的余项或余和.显然有 当n充分大时, 级数的敛散性它与部分和数列是否有 极限是等价的.  = + + ++ +  = n n un u1 u2 u3 u 1 (1) 称差 s s n  误差为 | | n r

例级数1+2+3++n+..的部分和n(n+1)S,=1+2+3+...+n=2n(n + 1)而lims, = lim82n-oon-→>所以，级数发散

例 2 ( 1) 1 2 3 + = + + + + = n n sn  n 而 = → n n lims 所以, 级数 1+ 2 + 3 ++ n + 的部分和 = + → 2 ( 1) lim n n n  级数发散

例讨论等比级数(几何级数)8Zaq" = a+aq+aq" +...+aq" +... (a* O)n=0的收敛性。(重要)解如果g1时1-Sn = a+aq+aq’ +...+aqna-aqaaq1-q1-q1-q

解 如果q  1 时 2 −1 = + + + + n sn a aq aq  aq q a aqn − − = 1 q aq q a n − − − = 1 1 (重要) 例 讨论等比级数(几何级数) 的收敛性. ( 0) 2 0  = + + + + +   = aq a aq aq aq a n n n  

naaqSn1-q1-qa当q80n-00当q|>1 时，： lim"= 0:. lims, = 00发散n-0n-0如果=1 时发散当g=1时, Sn = na →80当q=-1时,级数变为a-a+a-a+.发散:lim s.不存在n>当<时,收敛8Zag"综上当q≥1时,发散n=0

当q  1 时, lim = 0 → n n  q q a sn n −  = → 1 lim 当q  1 时, =  → n n lim q  =  → n n lims 收敛 发散 如果q = 1 时 当q = 1 时, 当q = −1 时, sn = na →  发散 a − a + a − a + n 不存在 n s → lim 发散 综上         = 当 时 发 散 当 时 收 敛 1 , 1 , 0 q q aq n n 级数变为 q aq q a s n n − − − = 1 1

8例讨论级数3ln"a(a>0)的敛散性>n=18Z3ln"a是以lna为公比的等比级数因为解n=1故当-<a<e时,Ilnakl,级数收敛.或a≥e时,llna≥l,发散当0<a≤=D当<1时,收敛8Zag"当≥1时,发散n=0

讨论级数 3ln ( 0) 的敛散性. 1    = a a n n 解 例 因为   =1 3ln n n a 是以 lna 为公比的等比级数, 故 , 1 当 a e时 e   | lna | 1, 级数收敛. 发散. e a 1 当0   | lna | 1,         = 当 时 发 散 当 时 收 敛 1 , 1 , 0 q q aq n n 或a  e时