《高等数学》课程教学资源（PPT课件）第十一章 曲线曲面积分 11-01 第一节 对弧长的曲线积分

第一节对弧长的曲线积分对弧长的曲线积分的概念与性质11 111 对弧长的曲线积分的计算法几何与物理意义四、小结思考题

第一节 对弧长的曲线积分 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 三、几何与物理意义 四、小结 思考题

对弧长的曲线积分的概念与性质一、1.引例曲线形构件的质量1B假设曲线形细长构件在空间所占弧段为AB其线密度为p(x,y,z),M(Ek,nk,Sh)AsM为计算此构件的质量,采用k-1“大化小,常代变,近似和,求极限”A1Zp(5k,n,S)Ask可得M =lim2>0k=1

A B 一、对弧长的曲线积分的概念与性质 假设曲线形细长构件在空间所占 弧段为AB , 其线密度为 “大化小,常代变,近似和,求极限” 可得 1 n k= M =  为计算此构件的质量, k s Mk −1 Mk ( , , ) k k k    1.引例 曲线形构件的质量 采用

2.定义设I是空间中一条有限长的光滑曲线，f(x,y,z)是定义在I上的一个有界函数(5k,nk,Sk)若通过对I的任意分割和对局部的任意取点下列“乘积和式极限M记作nlimEf(5k,nk,5h)AsAs f(x,y,z)dsM1-→0k-1k=1r

 设是空间中一条有限长的光滑曲线, 义在上的一个有界函数, ( , , ) k k k k f s     = 记作 f x y z s ( , , ) d   若通过对的任意分割 局部的任意取点, 2. 定义 下列“乘积和式极限” 1 n k= lim →0  k s Mk −1 Mk ( , , ) k k k 和对   

都存在,则称此极限为函数f(x,,z)在曲线厂上对弧长的曲线积分或第一类曲线积分f(x,y,z)称为被积函数,I称为积分弧段曲线形构件的质量M =_p(x,y,z)ds

都存在, 上对弧长的曲线积分, 则称此极限为函数 在曲线 或第一类曲线积分. 称为被积函数，称为积分弧段. 曲线形构件的质量 M x y z s ( , , ) d  = 

如果L是xoy面上的曲线弧,则定义对弧长的曲线积分为Zf(5n,n)Ask[,f(x,y)ds =lim1→0k=1如果 L是闭曲线,则记为Φ,f(x,y)ds.思考(1)若在L上f(x,y)=l，（,ds 表示什么 ？(2）定积分是否可看作对弧长曲线积分的特例?否！对弧长的曲线积分要求ds≥0,但定积分中dx可能为负

如果L是xoy面上的曲线弧, 0 1 lim ( , ) n k k k k f s    → =  L f x y s ( , )d =   如果 L是闭曲线, 则记为 ( , ) d . L f x y s  则定义对弧长的 曲线积分为 思考 (1) 若在L上 f(x,y)≡1, d ? L s  表示什么 (2) 定积分是否可看作对弧长曲线积分的特例? 否! 对弧长的曲线积分要求ds 0,但定积分中 dx可能为负

3.性质(1) J_[ f(x,y,z)±g(x,y,z)]ds= J, f(x, y,z)d s+J,g(x, y,z)ds(2) [,kf(x, y,z)d s =kJ, f(x,y,z)ds(k为常数)(3) [rf(x,y,z)ds =( f(x, y,z)ds+f(x, y,z)ds(T由1，I,组成)(4) J,ds=l(为曲线弧I的长度

3. 性质 (1) ( , , ) d  f x y z s    （k为常数) (3) ( , , ) d f x y z s   (由 组成) (l为曲线弧的长度)  g x y z ( , , ) f x y z s ( , , ) d  =  g x y z s ( , , ) d   1 2 f x y z s f x y z s ( , , ) d ( , , ) d   = +  

二、对弧长的曲线积分的计算法转化、计算定积分求曲线积分基本思路定理设f(x，）是定义在光滑曲线弧L: x=p(t ), y=y(t) (α≤t≤β)上的连续函数则曲线积分[,f(x,y) ds 存在，且f, f(x, y)ds = f f[o(t), y(t)No"(t)+y"(t) dt

2 2 ( , ) [ ( ), ( )] ( ) ( ) d L f x y ds f t t t t t   = +         二、对弧长的曲线积分的计算法 基本思路 转 化 计算定积分 定理 且 上的连续函数则曲线积分 , 求曲线积分 设 f x y ( , ) 是定义在光滑曲线弧

证根据定义Z f(5r,nk)AskJ, f(x,y)ds lim1→0k=1设各分点对应参数为t（k=0，1，…，n）点（，）对应参数为E【tk-1，t」，As = [r Vo'(t) +y"(t) d t= Vo"(th)+y'(t')Ath ,Th e[ th-1,th]

证 根据定义 0 1 lim ( , ) n k k k k f s    → = =   点 ( , ) k k   设各分点对应参数为 对应参数为 1 2 2 ( ) ( ) d k k t k t s t t t   −  = +    2 2 ( ) ( ) , k k k = +          t

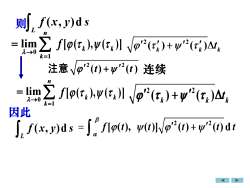
f(x,y)ds则n2 F[0(t ),V(t)] 0"(t)+"(t)Atlim一1→0k=1注意p"(t)+y"(t)连续nZ f[(t),V(t) /p"(tr)+y"(tr)Atlim1→0k=1因此J, f(x,J)ds =J f[o(t), y(t)Np"(t)+y"(1)dt

0 1 lim n k → = =  [ ( ), ( )] k k f     2 2 注 意     ( ) ( ) t t + 则 0 1 lim n k → = =  [ ( ), ( )] k k f     因此 连续

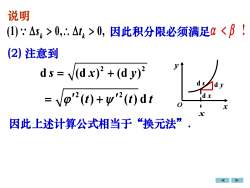
说明 0,.. △t, > 0, ，因此积分限必须满足α(2) 注意到ds = /(dx)* +(d y)dsdydx= Vp'(t) + y'2(t) d t01xx“换元法”因此上述计算公式相当于

d x d d y s x y o 说明 (1) 0, 0, k k      s t 因此积分限必须满足    ! (2) 注意到 2 2 d (d ) (d ) s x y = + 2 2 = +     ( ) ( ) d t t t x 因此上述计算公式相当于“换元法