《概率论与数理统计》课程教学资源（电子教案）第4章 随机变量的函数

第4章随机变量的函数4.1一维随机变量函数的分布内容：一维随机变量函数的分布一、离散型随机变量的函数的分布；二、连续型随机变量的函数的分布教学目标及基本要求掌握简单的随机变量函数概率分布的求解方法重点：随机变量函数的分布难点：求随机变量函数的分布律、分布函数、概率密度一般地，若X是分布已知的随机变量，g(x）为一元连续函数，那么由Y=g(X)定义的Y也是一个随机变量.按定义，Y=g(X)的分布函数应为：Fy(y)= P(Y≤y)= P(g(X)≤y)下面我们就依据上式，讨论如何由已知的随机变量X的分布去求它的函数Y=g(X)的分布一、离散型随机变量的函数的分布例1：设随机变量X具有以下分布律：-1012福X0.20.30.10.4求随机变量Y=(X-1)的分布律解：Y所有可能取的值为0，1，4.由P(Y = 0) = P((X -1) = 0) = P(X = 1) = 0.1 ,P(Y=1)=P(X=0)+P(X=2)=0.7,P(Y = 4) = P(X = -1) = 0.2 ,即得Y的分布律为014X0.10.70.2

第 4 章 随机变量的函数 4.1 一维随机变量函数的分布 内容：一维随机变量函数的分布 一、离散型随机变量的函数的分布； 二、连续型随机变量的函数的分布. 教学目标及基本要求 掌握简单的随机变量函数概率分布的求解方法. 重点：随机变量函数的分布 难点：求随机变量函数的分布律、分布函数、概率密度 一般地，若 X 是分布已知的随机变量， g x( ) 为一元连续函数，那么由 Y = g X( )定义的Y 也是一个随机变量.按定义，Y = g X( )的分布函数应为： ( ) { } { ( ) } FY y = P Y £ y = £ P g X y 下面我们就依据上式，讨论如何由已知的随机变量 X 的分布去求它的函数 Y = g X( )的分布. 一、离散型随机变量的函数的分布 例 1：设随机变量 X 具有以下分布律： 1 0 1 2 0.2 0.3 0.1 0.4 X é ù - ê ú ë û 求随机变量 2 Y X = - ( 1) 的分布律. 解： Y 所有可能取的值为 0，1，4.由 2 P{Y = 0} = P{(X -1) = 0} = P X{ = = 1} 0.1， P{Y =1} = P{X = 0}+ P X{ = = 2} 0.7 ， P{Y = 4} = P X{ = - = 1} 0.2 ， 即得Y 的分布律为 0 1 4 0.1 0.7 0.2 X é ù ê ú ë û

例2：设随机变量X的分布律为1P(X = k) =k=1,2,..2k求随机变量Y=sin( x)的分布律.2解：随机变量Y=sin(x)的可能取值有三个：-1，0，1.取各可能值的概率2分别为P(Y=0)=ZP(X =2k)=2=台22k=3K=lP(Y=-1)=2P(X=4k-1)=2,1-=2合124k-115合87.1P(Y =1)=ZP(X = 4k-3)= )24-315K于是得到随机变量Y的分布律为0-11Y = sin( x)8212L15315 二、连续型随机变量函数的分布例3：设随机变量X服从N(O,I)，求Y=X的分布密度解：由Y=X2，所以当y0时，F())= P(X? ≤以= P(-/≤X≤/)-de2dJ-2元J02元对F(y)求导即知此时Y=X?的分布密度为d.-2fr()=-F,(y) =dy/2元y当y=0时，作为密度在个别点的值可任意规定.如取f,(0)=0综上所述，Y=X?的分布密度为

例 2：设随机变量 X 的分布律为 1 { } 2 k P X k = = k =1, 2,L 求随机变量 sin( ) 2 Y X p = 的分布律. 解：随机变量 sin( ) 2 Y X p = 的可能取值有三个：-1，0，1.取各可能值的概率 分别为 2 1 1 1 1 { 0} { 2 } 2 3 k k k P Y P X k ¥ ¥ = = = = å å = = = 4 1 1 1 1 2 { 1} { 4 1} 2 15 k k k P Y P X k ¥ ¥ - = = = - =å å = - = = 4 3 1 1 1 8 { 1} { 4 3} 2 15 k k k P Y P X k ¥ ¥ - = = = = å å = - = = 于是得到随机变量Y 的分布律为 sin( ) 2 Y X p = 1 0 1 218 15 3 15 é ù - ê ú ê ú ë û 二、连续型随机变量函数的分布 例 3：设随机变量 X 服从 N(0,1) ，求 2 Y X = 的分布密度. 解：由 2 Y X = ，所以当 y 0时， 2 2 2 2 2 0 ( ) { } { } 1 2 2 2 Y x x y y y F y P X y P y X y e dx e dx p p - - - = £ = - £ £ = = ò ò 对 ( ) F y Y 求导即知此时 2 Y X = 的分布密度为 2 1 ( ) ( ) 2 y Y Y d f y F y e dy p y - = = 当 y = 0时，作为密度在个别点的值可任意规定.如取 (0) 0 Y f = . 综上所述， 2 Y X = 的分布密度为

>0fr(y):12元0,y≤o根据上述例题，可以得出在已知X的分布密度f(x）时，求随机变量函数Y=g(X)的分布密度的步骤：（1）根据X的分布密度f(x)计算出Y=g(X)的分布函数F(y) = P(g(X)≤y)(2）对F(y)求导即得Y=g(X)的分布密度：dP(g(X)≤y)Jr()=dy并且可得以下定理定理1若X服从正态分布Nu.α），则Y=aX+b服从正态分布N(aμ+b,a")证（以a>0为例证明）设Y的分布函数为F(y)，则F()= P(aX +b≤)= P(X ≤-b)a(x-μ)12gdxV2元求导即知Y的密度函数为[r-(aμ+b)P1d2(a0)2fr(y)=Fy(y)=V2元a0dy亦即Y=aX+b服从正态分布N(au+b,a)在定理1中令α=1/,b=-μ/α，则可得下面的定理定理2若X服从正态分布N(u,o")，则Y=X-μN(0,1)a例4设X服从N1.5.4），利用定理2计算(1) P(|X -1.5|>2);(2) P(X|≤1)

2 1 , 0 ( ) 2 0 , 0 y Y e y f y y y p ì - ï > = í ï î £ 根据上述例题，可以得出在已知 X 的分布密度 f x( ) 时，求随机变量函数 Y = g X( )的分布密度的步骤： （1） 根据 X 的分布密度 f x( ) 计算出Y = g X( )的分布函数 ( ) { ( ) } FY y = £ P g X y （2） 对 ( ) F y Y 求导即得Y = g X( )的分布密度： ( ) { ( ) } Y d f y P g X y dy = £ 并且可得以下定理. 定理 1 若 X 服从正态分布 2 N(m s, ) ，则 Y = + aX b 服从正态分布 2 2 N(am s + b a, ). 证 （以a > 0为例证明）设Y 的分布函数为 ( ) F y Y ，则 2 2 ( ) 2 ( ) { } { } 1 2 Y y b x a y b F y P aX b y P X a e dx m s ps - - - -¥ - = + £ = £ = ò 求导即知Y 的密度函数为 2 2 [ ( )] 1 2( ) ( ) ( ) 2 y a b a Y Y d f y F y e dy a m s p s - + - = = 亦即Y = + aX b服从正态分布 2 2 N(am s + b a, ). 在定理 1 中令 a b =1/s, / = -m s ，则可得下面的定理. 定理 2 若 X 服从正态分布 2 N(m s, ) ，则 (0,1) X Y N m s - = . 例 4 设 X 服从 N(1.5,4) ，利用定理 2 计算 （1） P X{ - > 1.5 2}； （2） P X{ £1}

解：定理2知-1.5N(O,I).再利用分布函数Φ(x)的对称性即公式2Φ(-x)=1-Φ(x)并查附表3即得(1) P(x-15)>2)=P|=15>1=2(-1)n= 2[1Φ(1)] = 2 ×(1 0.8413) = 0.3174(-1-1.5], X-1.5 ,1-15) = 0(-0.25) (-1.25)(2) P(X≤1)=P(222=-Φ(0.25)+Φ(1.25)=-0.5987+0.8944=0.2957还可证明以下定理定理3设X是以f(x)为分布密度的连续型随机变量，其所有可能取值构成区间I，函数y=g(x)在区间I上严格单调可微，g(I)为相应的值域，则函数Y=g(X)也是一个连续型随机变量且分布密度为df[g"(y)]]18oyeg(I)fr(y)=其他0,其中x=g-(y)是y=g(x)的反函数例5设随机变量X的分布密度为2x>0F(x)= 元(1+x3)[0,x≤0求Y=lnX的分布密度解：显然y=lnx在(0,+o)上严格单调可微且其反函数为x= g-'(y)=er,E(-00,+8)故由定理3知Y=lnX的分布密度为2elf,(y)= f[g"(v)]-g"()= f(e')e=-元(I+e3), ye(-00, +o0)d

解：定理 2 知 1.5 (0,1) 2 X N - .再利用分布函数 f( ) x 的对称性即公式 f f (-x x ) = -1 ( ) 并查附表 3 即得 （1） 1.5 { 1.5 2} { 1} 2 ( 1) 2 X P X P f - - > = > = - = 2[1-f(1)] = 2´(1- = 0.8413) 0.3174 （2） 1 1.5 1.5 1 1.5 { 1} { } ( 0.25) ( 1.25) 2 2 2 X P X P f f - - - - £ = £ £ = - - - = -f f (0.25) + (1.25) = -0.5987 + = 0.8944 0.2957 还可证明以下定理. 定理 3 设 X 是以 f x( ) 为分布密度的连续型随机变量，其所有可能取值构 成区间 I ，函数 y = g x( ) 在区间 I 上严格单调可微， g I( )为相应的值域，则函数 Y = g X( )也是一个连续型随机变量且分布密度为 1 1 [ ( )] ( ) , ( ) ( ) 0, Y d f g y g y y g I f y dy - - ì ï Î = í ï î 其他 其中 1 x g y( ) - = 是 y = g x( ) 的反函数. 例 5 设随机变量 X 的分布密度为 2 2 , 0 ( ) (1 ) 0, 0 x f x x x p ì ï > = í + ï î £ 求Y X = ln 的分布密度. 解：显然 y x = ln 在(0, ) +¥ 上严格单调可微且其反函数为 1 ( ) , ( , ) y x g y e y - = = Î -¥ +¥ 故由定理 3 知Y X = ln 的分布密度为 1 1 2 2 ( ) [ ( )] ( ) ( ) , ( , ) (1 ) y y y Y y d e f y f g y g y f e e y dy e p - - = = = Î -¥ +¥ +

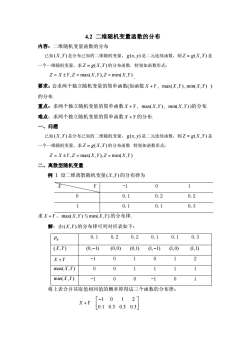
4.2二维随机变量函数的分布内容：二维随机变量函数的分布已知(X,Y)是分布已知的二维随机变量，g(x,J)是二元连续函数，则Z=g(X,Y)是一个一维随机变量，求Z=g(X,Y)的分布函数。特别如函数形式：Z=X±Y,Z=max(X,Y),Z=min(X,Y)要求：会求两个独立随机变量的简单函数(如函数X+Y，max(X,Y),min(X,Y））的分布.重点：求两个独立随机变量的简单函数X+Y，max(X,Y)，min(X,Y))的分布难点：求两个独立随机变量的简单函数X+Y的分布.一、问题已知(X,Y)是分布已知的二维随机变量，g(x,y)是二元连续函数，则Z=g(X,Y)是一个一维随机变量，求Z=g(X,Y)的分布函数。特别如函数形式：Z = X±Y,Z =max(X,Y),Z=min(X,Y)二、离散型随机变量例1设二维离散随机变量(X,Y)的分布律为Y0X-1100. 10.20.210.10. 10.3求X+Y，max(X,Y)与min(X,Y)的分布律.解：由(X,Y)的分布律可列对应表如下：0. 10. 20. 20. 10. 10. 3Pu(X,Y)(0,-1)(0,0)(0,1)(1, -1)(1,0)(1,1)-101012X+Y001111max(X,Y)000min(X,Y)-1-11将上表合并其取值相同值的概率即得这三个函数的分布律：021-1X+Y0.100.30.30.3

4.2 二维随机变量函数的分布 内容：二维随机变量函数的分布 已知(X Y, ) 是分布已知的二维随机变量， g(x y, ) 是二元连续函数，则 Z = g(X Y, ) 是 一个一维随机变量，求Z = g(X Y, ) 的分布函数. 特别如函数形式： Z = X ±Y,Z = = max(X ,Y), Z min(X Y, ) . 要求：会求两个独立随机变量的简单函数(如函数 X Y+ , max(X Y, ) , min(X Y, ) ) 的分布. 重点：求两个独立随机变量的简单函数 X Y+ , max(X Y, ) , min(X Y, ) )的分布. 难点：求两个独立随机变量的简单函数 X Y+ 的分布. 一、问题 已知(X Y, ) 是分布已知的二维随机变量， g(x y, ) 是二元连续函数，则 Z = g(X Y, ) 是 一个一维随机变量，求Z = g(X Y, ) 的分布函数. 特别如函数形式： Z = X ±Y,Z = = max(X ,Y), Z min(X Y, ) . 二、离散型随机变量 例 1 设二维离散随机变量(X Y, ) 的分布律为 X Y -1 0 1 0 0.1 0.2 0.2 1 0.1 0.1 0.3 求 X Y+ ， max(X Y, ) 与min(X Y, ) 的分布律. 解：由(X Y, ) 的分布律可列对应表如下： ij p 0.1 0.2 0.2 0.1 0.1 0.3 (X Y, ) (0,-1) (0,0) (0,1) (1,-1) (1,0) (1,1) X Y+ -1 0 1 0 1 2 max(X Y, ) 0 0 1 1 1 1 min(X Y, ) -1 0 0 -1 0 1 将上表合并其取值相同值的概率即得这三个函数的分布律： 1 0 1 2 0.1 0.3 0.3 0.3 X Y é ù - + ê ú ë û

0max(X,Y)0.30.701min(X,Y)0.20.50.3三、连续型随机变量1、和的分布设二维随机变量(X,Y)的分布密度为f(x,J)，求Z=X+Y的分布密度由假设，Z=X+Y的分布函数为：Fz(2)= P(X+Y≤z)= JT (x,y)dxdy= t[f" f(x, )dyldx=t[f (x,t-x)dij]dx(变换y = t-x)= "ft (x, - x)dxJdt对函数Fz(=)求导，得Z=X+Y的分布密度：J2(=)= [ f(x,z- x)dx由X，Y的对称性，Z=X+Y的分布密度又可写成f2(2)= t f(z-y,y)dy特别地，当X与Y独立时，上述两式可写成：f(2)=[ fx(n)f(z-x)dx(卷积公式)J2(=)= [ fx(2-y)f,(v)dy(卷积公式)例2设随机变量X与Y相互独立，其分布密度分别为[1, 0<x<1,[2y, 0<y<1Jx(x)=fr(y)=[o，其他，10，其他求Z=X+Y的分布密度.解：由卷积公式知，Z=X+Y的分布密度为fz(a)= [ x(x)fr(z-x)dx=[ fr(=-x)dx=-[ f(t)di(变换z-x=t)

0 1 max( , ) 0.3 0.7 X Y é ù ê ú ë û 1 0 1 min( , ) 0.2 0.5 0.3 X Y é ù - ê ú ë û 三、连续型随机变量 1、和的分布 设二维随机变量(X Y, ) 的分布密度为 f (x y, ) ，求Z = + X Y 的分布密度. 由假设，Z = + X Y 的分布函数为： ( ) { } ( , ) [ ( , ) ] z x Z x y z F z P X Y z f x y dxdy f x y dy dx +¥ - -¥ -¥ + £ = + £ = = òò ò ò [ ( , ) ] ( ) z f x t x dt dx y t x +¥ -¥ -¥ = - = - ò ò 变换 [ ( , ) ] z f x t x dx dt +¥ -¥ -¥ = - ò ò 对函数 ( ) F z Z 求导，得Z = + X Y 的分布密度： ( ) ( , ) Z f z f x z x dx +¥ -¥ = - ò 由 X ，Y 的对称性，Z = + X Y 的分布密度又可写成 ( ) ( , ) Z f z f z y y dy +¥ -¥ = - ò 特别地，当 X 与Y 独立时，上述两式可写成： ( ) ( ) ( ) ( ) Z X Y f z f x f z x dx +¥ -¥ = - ò 卷积公式 ( ) ( ) ( ) ( ) Z X Y f z f z y f y dy +¥ -¥ = - ò 卷积公式 例 2 设随机变量 X 与Y 相互独立，其分布密度分别为 1, 0 1 ( ) 0, X x f x ì < < = í î ， 其他， 2 , 0 1 ( ) 0, Y y y f y ì < < = í î 其他 求Z = + X Y 的分布密度. 解：由卷积公式知，Z = + X Y 的分布密度为 1 1 0 ( ) ( ) ( ) ( ) ( ) ( ) z Z X Y Y Y z f z f x f z x dx f z x dx f t dt t +¥ - -¥ = - = - = - = ò ò ò 变换z-x

[2tdt,0SCX亦服从正态分1=1Zcx,之c，其中CC,,为任意常数布，且N(ZC,H,2Ai=i=li=l2）最大值与最小值的分布X与Y相互独立，且其分布函数分别为Fx(x)和F(y)，求max(X,Y)与min(X,Y)的分布函数max(X,Y)的分布函数为

2 0 1 2 1 1 2 , 0 1 , 0 1 ( ) 2 , 1 2 2 ,1 2 0, 0, z z Y z z tdt z z z f t dt tdt z z z z - - ì < £ ï ì < £ ï ï = = í í < £ = - < £ ï ï ï î î ò ò ò 其他 其他 定理 1 设 2 1 1 X N(m s, )， 2 2 2 Y N(m s, ) 且相互独立，则 Z = + X Y 亦服从 正态分布，且 2 2 1 2 1 2 X +Y N(m + + m , ) s s . 证： 由卷积公式知，Z = + X Y 的分布密度为 2 2 1 2 2 2 1 2 1 2 1 ( ) ( ) ( ) exp[ ] 2 2 2 Z x z x f x dx m m ps s s s +¥ -¥ - - - = - - ò 2 2 2 2 2 2 2 1 2 1 2 1 2 1 1 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 ( ) exp[ ] 2 2( ) 2 z z x dx m m s s s m s m s ps s s s s s s s +¥ -¥ - - + æ ö - - = - - - ç ÷ + + è ø ò 在上式作变量替换 2 2 2 1 2 1 1 2 1 2 2 2 2 2 1 2 1 2 z x t s m s m s s s s s s s - - - = + + 有 2 2 2 1 2 1 2 2 2 2 2 1 2 1 2 ( ) ( ) 2( ) 2( ) 2 2 2 2 2 1 2 1 2 1 1 1 ( ) 2 2 2 z z t Z f z e e dt e m m m m s s s s p s s p p s s - - - - - - - + + = = + + ò 即 2 2 1 2 1 2 Z = X +Y N 服从 (m + + m , ) s s . 定理 2 （独立正态分布的线性组合定理）设 1 2 , , , X X X L n 相互独立且分别服从 正态分布即 2 ( , ) ( 1,2, ) Xi N i i L m s i n = ，则它们的线性组合 1 n i i i C X = å 亦服从正态分 布，且 2 2 1 1 1 ( , ) n n n i i i i i i i i i C X N C C m s = = = å å å ,其中 1 2 , , , C C C L n 为任意常数. 2）最大值与最小值的分布 X 与Y 相互独立，且其分布函数分别为 ( ) F x X 和 ( ) F y Y ，求 max(X Y, ) 与 min(X Y, ) 的分布函数. max(X Y, ) 的分布函数为

Fmax (2)= P(max(X,Y)≤z) = P(X≤z,Y≤z)= P(X≤z)P(Y≤2)即由Fmax (z)= Fr(2)F,(2)同理,min(X,Y)的分布函数为Fmn(2)= P(min(X,Y)≤z) = P(X≤z或Y ≤z) =1-P(X>z,Y >z)=1-P(X >2)P(Y >z) =1-[1- P(X ≤z)][1- P(Y≤z)]即有Fmin(2) =1-[1- Fx(-)[1- F,(-)]对于n个相互独立的随机变量的情形设X,X2,,X,是n个相互独立的随机变量，其分布函数分别为Fx(x),Fx2(x2),--,Fx (x)则max(X,X2,"",X）与min(X,X2,""X）的分布函数为Fmax (2) = Fx (=)Fx,(2).. Fx, (2)Fmn(=)=1-[1-Fx (2)[1- Fx (2)]- [1- Fx (2)]特别地，当X,X,,X,相互独立且具有相同分布函数F(x)时，Fmx (2) =[F(=)"Fmn(-) =1-[1- F(2)]例3某电子仪器由六个相互独立的部件L（k=1,2,…·6)组成，其连接方式如图所示.设各个部件的使用寿命X，服从相同的指数分布e(2)，求仪器使用寿命X的概率分布密度解：各个部件的使用寿命X,(k=1,2,.6)的分布函数均为：[1-e-x,x>0F(x) =[0,x≤0由图知，仪器的使用寿命X与各部件的使用寿命X，由如下关系：

max F (z) = P{max(X ,Y ) £ z} = P{X £ z,Y £ z} = P{X £ £ z}P{ } Y z 即由 max ( ) ( ) ( ) F X Y z = F z F z 同理,min(X Y, ) 的分布函数为 min ( ) {min( , ) } { } 1 { , } 1 { } { } 1 [1 { }][1 { }] F z P X Y z P X z Y z P X z Y z P X z P Y z P X z P Y z = £ = £ £ = - > > = - > > = - - £ - £ 或 即有 min ( ) 1 [1 ( )][1 ( )] F X Y z = - - - F z F z 对于n 个相互独立的随机变量的情形. 设 1 2 , , , X X X L n 是n 个相互独立的随机变量，其分布函数分别为 1 1 2 2 ( ), ( ), , ( ) X X X n n F x F x L F x 则max ( X1 2 , X X , , L n ) 与min ( X1 2 , X X , , L n ) 的分布函数为 m 1 2 ax ( ) ( ) ( ) ( ) X X Xn F z = F z F z LF z m 1 2 in ( ) 1 [1 ( )][1 ( )] [1 ( )] X X Xn F z = - - F z - - F z L F z 特别地，当 1 2 , , , X X X L n 相互独立且具有相同分布函数 F x( )时， max ( ) [ ( )]n F z = F z min ( ) 1 [1 ( )]n F z = - - F z 例 3 某电子仪器由六个相互独立的 部件 ( 1, 2, 6) L k k = L 组成，其连接方式 如图所示.设各个部件的使用寿命 Xk 服 从相同的指数分布e( ) l ，求仪器使用寿命 X 的概率分布密度. 解：各个部件的使用寿命 ( 1, 2, 6) X k k = L 的分布函数均为： 1 , 0 ( ) 0, 0 x e x F x x -l ì - > = í î £ 由图知，仪器的使用寿命 X 与各部件的使用寿命 Xk 由如下关系： L4 L5 L6 L1 L2 L3

X = max(min(X,X2,X,),min(X4,X,,X.))故按公式得仪器的使用寿命X的分布函数为Fx(x)=[1-[1- F(x)}][[1-[1-(1-e-)}P, x>0[0,x≤0 (1-e-3r)2,x>0=[0,x≤0求导即得仪器使用寿命X的分布密度为[61e-3*(1-e-3^r),x>0fx(x)=[0,x≤0

m 1 2 3 456 X = ax{min(X , X , X ),min(X , X X, )} 故按公式得仪器的使用寿命 X 的分布函数为 3 2 3 2 3 2 ( ) [1 [1 ( )] ] [1 [1 (1 )] ] , 0 0, 0 (1 ) , 0 0, 0 X x x F x F x e x x e x x l l - - = - - ì - - - > = í î £ ì - > = í î £ 求导即得仪器使用寿命 X 的分布密度为 3 3 6 (1 ), 0 ( ) 0, 0 x x X e e x f x x l l l - - ì - > = í î £